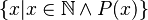Induction proof
From Event-B
This page explains how to proove with induction method on the natural number with Rodin tools.
In other words, how to proove :
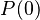
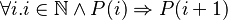
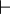
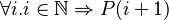
The proof key is the following theorem:
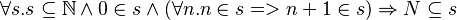
The proof of the previous theorem is given by the following.
Instanciate the key theorem with :