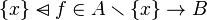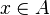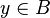Maplet Overriding in Goal

This page describes the design of a tactic requested here : Feature Request #3306228

Objective

Split every goal in the form : 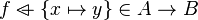$f \ovl{\{x \mapsto y\}} \in A \to B$ into three sub-goals :

• $\{x\} \domsub f \in A \smallsetminus \{x\} \to B$
• $x \in A$
• $y \in B$

Design Decision

Instead of proofing the first sub-goal, it may be more easy to proof 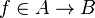$f\in A\to B$ which is a sufficient condition : $(f\in A\to B)\limp (\{x\} \domsub f \in A \smallsetminus \{x\} \to B)$.

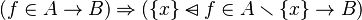Implementation

First, the goal is checked. Its tree structure must match the following one :

$\in$
├── $\ovl$
│   ├── f
│   └── {}
│       └──  $\mapsto$
│            ├── x
│            └── y
└── $\to$
    ├── A
    └── B

Then, if the hypothesis 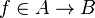$f\in A\to B$ is present, the goal is split as follows :

• $f\in A\to B$
• $x \in A$
• $y \in B$

Else, it is split as follows :

• $\{x\} \domsub f \in A \smallsetminus \{x\} \to B$
• $x \in A$
• $y \in B$