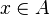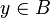Maplet Overriding in Goal

This page describes the design of a tactic requested here : Feature Request #3306228

Objective

Split every goal in the form : 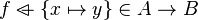$f\ovl{\{x\mapsto y\}}\in A\to B$ into three sub-goals if and only if the sequent contains that hypothesis $f\in A\;op\;B$ :

• $f\in A\;op\;B$
• $x\in A$
• $y\in B$

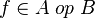Where 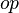$op$ denote either a Relation 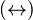$\left(\rel\right)$, or a Total Relation 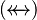$\left(\trel\right)$, or a Partial Function 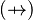$\left(\pfun\right)$, or a Total Function $\left(\tfun\right)$.

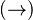Design Decision

Those three subgoals are not equivalent to the goal from which they are inferred. In order to get the equivalence, we should write 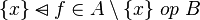$\{x\}\domsub f\in A\setminus\{x\}\;op\;B$. But this has the drawback of writing twice the expression x. If this expression is big, then it can make the proof rule hard to read.

But, we know that 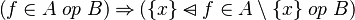$\left(f\in A\;op\;B\right)\limp \left(\{x\}\domsub f\in A\setminus\{x\}\;op\;B\right)$. By ensuring that this predicate is among the hypotheses of the sequent, we are sure that it will be proofed. Indeed, if this check was not done, the proof obligation may be unprovable since there are a loss of informations by writing 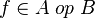$f\in A\;op\;B$ instead of $\{x\}\domsub f\in A\setminus\{x\}\;op\;B$.

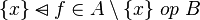Implementation

First, the goal is checked. Its tree structure must match the following one :

$\in$
├── $\ovl$
│   ├── f
│   └── {}
│       └──  $\mapsto$
│            ├── x
│            └── y
└── $op$
    ├── A
    └── B

Then, if the hypothesis 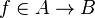$f\in A\to B$ is present, the goal is split as follows :

• $f\in A\;op\;B$
• $x \in A$
• $y \in B$

Else nothing is proceeded.