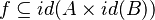Mathematical Language Evolution Design

Introduction

This document describes the modifications that occur to the Event-B mathematical language from the developer point of view. The old language will still be recognized, in order to provide backward compatibility.

These changes are described from a user point of view in Changes to the Mathematical Language of Event-B.

Syntax Tree

Deprecated nodes (becoming atomic expressions):

• KPRJ1
• KPRJ2
• KID

New nodes:

• KPARTITION that represents the new partition predicate (relational predicate)
• KPRJ1_GEN that represents the atomic version of the first projection
• KPRJ2_GEN that represents the atomic version of the second projection
• KID_GEN that represents the atomic version of the identity

Parser Changes

The new parser has a version attribute. Depending on the version, formulas are parsed differently. Thus, the KPARTITION node is a regular identifier if version is V1. It is accepted as a keyword only from version V2. Concerning, identity and projections, they are recognized as non-generic with V1 and generic with V2. The following table summarizes how tokens are processed depending on the parser version:

Token Recognition

	Parser V1	Parser V2
"partition"	IDENT	KPARTITION
"id"	KID	KID_GEN
"prj1"	KPRJ1	KPRJ1_GEN
"prj2"	KPRJ2	KPRJ2_GEN

Parsing

FormulaFactory has new parse() methods with a parser version argument. Existing methods default to the first version (ParserVersion.V1), while becoming deprecated. Thus, one now has to know, before parsing a formula, the version of the language it has been written with.

TODO: How to get the version from the file

Multiple Predicates / Partition

A new predicate class is introduced: MultiplePredicate that is abstract and superclasses Partition. A MultiplePredicate is a predicate that applies to a list of two or more expressions. In a Partition, all expressions must have the same type, that is the type of the partitioned set (first child).

Associativity

TODO

Visitors

IVisitor has three more methods:

• enter KPARTITION
• continue KPARTITION
• exitKPARTITION

ISimpleVisitor has one more method:

• visitMultiplePredicate

Sequent Prover

TODO

Affected client code

TODO

Upgrade

Formulas written with version V1 will need upgrading to version V2. However, most of the V1 formulas will be exactly the same with V2. A formula needs ugrading if:

• it contains one of {KPRJ1, KPRJ2, KID}
• it contains a non parenthesised sequence of relational set operators

In these cases an upgrade procedure will be applied to the formula using a IFormulaRewriter, to rewrite KPRJ1, KPRJ2, KID expressions into their generic equivalent (see Changes to the Mathematical Language of Event-B#Generic Identity and Projections).

Formatting

Ideally, upgrading a formula would preserve its previous formatting (spaces, tabs, new lines). But this turns out being quite tricky. Indeed, it prevents from simply rewriting the formula then applying a toString(), as this would totally forget and override any formatting. Thus, we would have to write directly into the original string. Firstly find the source locations where changes will occur, then patching the formula with the new expression versions at those source locations.

But that leads to more complexity when we come to consider formulas that contain

• recursive relational set operators (that recursively shift source locations)
• binary operators with higher priorities nearby (that mindlessly absorb a member of the rewritten expression)

Let's look at the following formula:

$f \sube id(A \times id(B))$

A straight rewriting would proceed as follows:

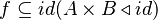• $f \sube id(A \times B \triangleleft id)$ which already is false (requires parentheses)

Then, with the appropriate shift of the source location to replace the first 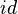$id$ operator:

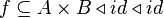• $f \sube A \times B \triangleleft id \triangleleft id$ which is even worse

This suggests putting parentheses around rewritten expressions. But they would sometimes be superfluous, which brings us to distinguish cases where they are needed and cases where they are not, depending on the priority of the operators nearby.

Considering this is going quite far, a simpler upgrade method is applied:

• if the formula does not use deprecated expressions, nor lacks parentheses around relational set operators, it is left unchanged, preserving the formatting
• it it does, it is rewritten and any previous formatting is overridden