Proof Manager
The Proof Manager is responsible for constructing proofs and maintaining existing proofs associated with proof obligations.
Overview
Proof obligations are generated by the proof obligation generator and have the form of sequents.
Sequents are proved using proof rules.
The Proof Manager architecture is separated into two parts: extensible part and static part. The extensible part is responsible for generating individual proof rules. The static part is responsible for putting proof rules together to construct and manage proofs. We call components that generate valid proof rules reasoners.
The basic reasoning capabilities of the Proof Manager can be extended by adding new reasoners. A reasoner may implement a decision procedure for automated proof, or a derived rule schema for interactive proof.
By applying the generated proof rules by different reasoner, the Proof Manager builds a (partial) proof for an proof obligation by constructing proof trees.
In order to encapsulate frequently used proof construction and manipulation steps, the Proof Manager provides the concept of tactics. They provides high-level strategic proof manipulations. Adding new tactics is the second possibility for extending the Proof Manager.
Sequents
A sequent stands for something we want to prove.
Sequents are of the following form
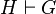
where H is the set of hypotheses (predicates) and G is the goal (a predicate in the mathematical language).
The meaning of the above sequent is that: Under the hypotheses H, prove the goal G.
Proof Rules
In its pure mathematical form, a proof rule is a tool to perform formal proof and is denoted by:
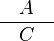
|
where A is a (possibly empty) list of sequents:the antecedents of the proof rule; and C is a sequent: the consequent of the rule. And we interpret the above proof rule as follows: The proofs of each sequent of A together give a proof of sequent C.
Representation
In Rodin, the representation for proof rules are more structure not only to reduce the space required to store the rule, but more importantly to support proof reuse.
A rule in Rodin contains the following:
- used goal A used goal predicate.
- used hypotheses The set of used hypotheses.
- antecedents A list of antecedents (to be explain later).
- reasoner the reasoner used to generate this proof rule (See reasoners).
- reasoner input the input to the reasoner to generate this proof rule (See reasoners).
Each antecedent of the proof rule contains the following information:
- new goal A new goal predicate.
- added hypotheses The set of added hypotheses.
With this representation, a proof rule in Rodin corresponding to a proof schema as follows:
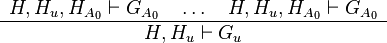
Where:
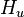 is the set of used hypotheses
is the set of used hypotheses
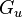 is the used goal
is the used goal
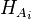 is the set of added hypotheses corresponding to the ith antecedent.
is the set of added hypotheses corresponding to the ith antecedent.
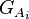 is the new goal corresponding to the ith antecedent.
is the new goal corresponding to the ith antecedent.
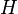 is the meta-variable that can be instantiated.
is the meta-variable that can be instantiated.
Applying Proof Rules
Given a proof rule of the form mentioned above, the following describes how to apply this rule to an input sequent. The result of this process is a list of output sequents if successful or null otherwise.
- The rule is applicable if the goal of the sequent is not exactly the same as the used goal or any of the used hypotheses is not contained in the set of hypotheses of the input sequent.
- In the case of applicable, the antecedent sequents are returned. The goal of each antecedent sequent is the new goal correspondingly. The hypotheses of each antecedent sequent is the union of the old hypotheses and added hypotheses of the corresponding antecedent.