Rewriting rules for event model decomposition
The purpose of this page is to list and justify the rewriting / simplification rules applied in the event model decomposition when building the external events, and more especially their actions.
Equivalence relation
It is possible to define an equivalence relation on the Event-B actions, and by restrictions on the Event-B assignments (an action is a set of assignments). Two actions are considered as being equivalent if the proof obligations generated for these actions are logically equivalent.
This relation is represented with the  symbol.
symbol.
Rewriting rules on Event-B assignments
As detailed in the modelling language, the Event-B assignments are formed of two parts:
- a left-hand side, which is a list of free identifiers.
- a right-hand side.
There are various kinds of assignments:
- The
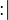 ("becomes such that") assignment is the most general (non-deterministic) assignment, where a predicate is given on the before and after values of assigned identifiers. The after values of the assigned identifiers are denoted by a primed identifier whose prefix is the assigned identifier.
("becomes such that") assignment is the most general (non-deterministic) assignment, where a predicate is given on the before and after values of assigned identifiers. The after values of the assigned identifiers are denoted by a primed identifier whose prefix is the assigned identifier. - The
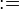 ("becomes equal to") assignment is the deterministic assignment where an expression is given for each assigned identifier.
("becomes equal to") assignment is the deterministic assignment where an expression is given for each assigned identifier. - The
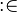 ("becomes member of") assignment is the set-based (non-deterministic) assignment, where a set expression is given for the assigned identifier.
("becomes member of") assignment is the set-based (non-deterministic) assignment, where a set expression is given for the assigned identifier.
Let 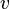 and
and 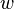 be variables, and
be variables, and 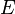 and
and 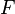 be expressions. In the following table, the left-hand assignments are equivalent (
be expressions. In the following table, the left-hand assignments are equivalent ( ) to the right-hand ones:
) to the right-hand ones:
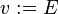 |
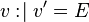 |
Rule 1 |
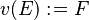 |
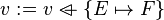 |
Rule 2 |
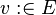 |
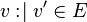 |
Rule 3 |
Thus, each Event-B assignment can be expressed in a "becomes such that" form, and more precisely as 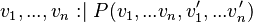 , where
, where 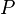 is a before-after predicate.
is a before-after predicate.
Rewriting rules on Event-B actions
Let 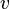 and
and 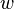 be variables,
be variables, 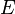 and
and 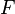 be expressions, and
be expressions, and 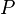 and
and 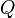 be predicates. The left-hand actions are equivalent (
be predicates. The left-hand actions are equivalent ( ) to the right-hand ones:
) to the right-hand ones:
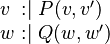 |
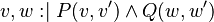 |
Rule 4 |
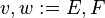 |
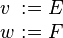 |
Rule 5 |
Simplification rules on Event-B predicates
Let 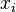 ,
, 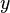 and
and 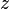 be variables, and
be variables, and 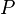 and
and 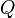 be predicates.
be predicates.
- Rule 6: If
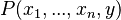 is equal to
is equal to 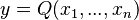 , then the
, then the 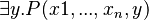 predicate is true, and it may be deleted in conjunctive predicates (
predicate is true, and it may be deleted in conjunctive predicates (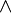 ) where it appears.
) where it appears. - Rule 7: The
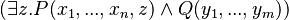 predicate, where
predicate, where 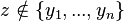 , may be rewritten as
, may be rewritten as 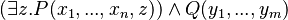 .
.
Simplification rules based on Event-B proof obligations
Example
Let 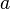 ,
, 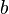 and
and 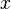 be variables, and
be variables, and 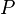 and
and 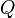 be predicates.
be predicates.
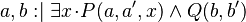
|
 (Rule 7) (Rule 7) |
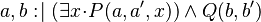
|
 (Rule 4) (Rule 4) |
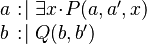
|