Arithmetic Rewrite Rules
From Event-B
| Name | Rule | Side Condition | A/M | |
|---|---|---|---|---|
| SIMP_SPECIAL_MOD_0 | 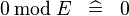 |
A | ||
| SIMP_SPECIAL_MOD_1 | 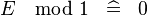 |
A | ||
| SIMP_MIN_SING | 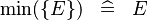 |
where  is a single expression is a single expression |
A | |
| SIMP_MAX_SING | 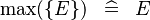 |
where  is a single expression is a single expression |
A | |
| SIMP_MIN_NATURAL | 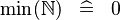 |
A | ||
| SIMP_MIN_NATURAL1 | 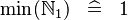 |
A | ||
| SIMP_MIN_BUNION_SING | 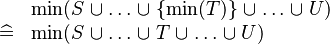 |
A | ||
| SIMP_MAX_BUNION_SING | 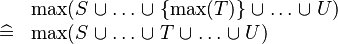 |
A | ||
| SIMP_MIN_UPTO | 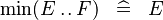 |
A | ||
| SIMP_MAX_UPTO | 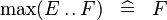 |
A | ||
| SIMP_LIT_MIN | 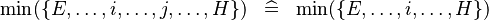 |
where  and and  are literals and are literals and 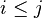 |
A | |
| SIMP_LIT_MAX | 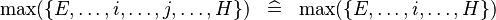 |
where  and and  are literals and are literals and 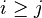 |
A | |
| SIMP_LIT_MIN_UPTO | 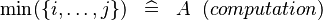 |
where 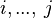 are literals are literals |
A | |
| SIMP_LIT_MAX_UPTO | 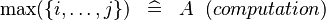 |
where 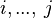 are literals are literals |
A | |
| SIMP_SPECIAL_CARD | 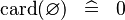 |
A | ||
| SIMP_CARD_SING | 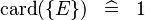 |
where  is a single expression is a single expression |
A | |
| SIMP_SPECIAL_EQUAL_CARD | 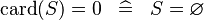 |
A | ||
| SIMP_CARD_POW | 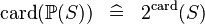 |
A | ||
| SIMP_CARD_BUNION | 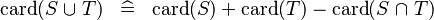 |
A | ||
| SIMP_CARD_CONVERSE | 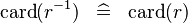 |
A | ||
| SIMP_CARD_ID | 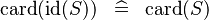 |
A | ||
| SIMP_CARD_LAMBDA | 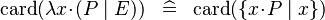 |
A | ||
| SIMP_CARD_COMPSET | 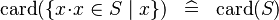 |
where  non free in non free in  |
A | |
| SIMP_LIT_CARD_UPTO | 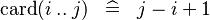 |
where  and and  are literals and are literals and 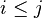 |
A | |
| SIMP_TYPE_CARD | 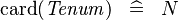 |
where 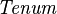 is a carrier set containing is a carrier set containing 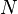 elements elements |
A | |
| SIMP_LIT_GE_CARD_0 | 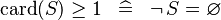 |
A | ||
| SIMP_LIT_LE_CARD_1 | 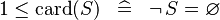 |
A | ||
| SIMP_LIT_LE_CARD_0 | 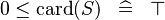 |
A | ||
| SIMP_LIT_GE_CARD_0 | 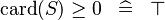 |
A | ||
| SIMP_LIT_GT_CARD_0 | 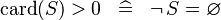 |
A | ||
| SIMP_LIT_LT_CARD_0 | 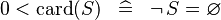 |
A | ||
| SIMP_LIT_EQUAL_CARD_1 | 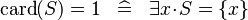 |
A | ||
| SIMP_CARD_NATURAL | 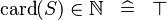 |
A | ||
| SIMP_CARD_NATURAL1 | 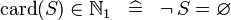 |
A | ||
| SIMP_LIT_IN_NATURAL |  |
where  is a literal is a literal |
A | |
| SIMP_SPECIAL_IN_NATURAL1 | 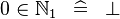 |
A | ||
| SIMP_LIT_IN_NATURAL1 | 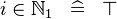 |
where  is a literal and is a literal and 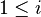 |
A | |
| SIMP_LIT_UPTO | 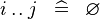 |
where  and and  are literals and are literals and 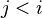 |
A | |
| SIMP_LIT_IN_MINUS_NATURAL | 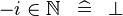 |
where  is a literal and is a literal and 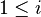 |
A | |
| SIMP_LIT_IN_MINUS_NATURAL1 | 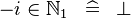 |
where  is a literal is a literal |
A | |
| SIMP_SPECIAL_KBOOL_BTRUE | 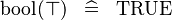 |
A | ||
| SIMP_SPECIAL_KBOOL_BFALSE | 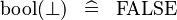 |
A | ||
| SIMP_LIT_EQUAL_KBOOL_TRUE | 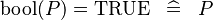 |
A | ||
| SIMP_LIT_EQUAL_KBOOL_FALSE | 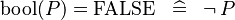 |
A | ||
| DEF_EQUAL_MIN | 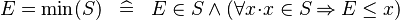 |
where  non free in non free in 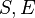 |
M | |
| DEF_EQUAL_MAX | 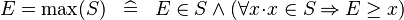 |
where  non free in non free in 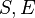 |
M | |
| SIMP_SPECIAL_PLUS | 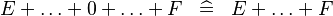 |
A | ||
| SIMP_SPECIAL_MINUS_R |  |
A | ||
| SIMP_SPECIAL_MINUS_L | 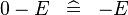 |
A | ||
| SIMP_MINUS_MINUS | 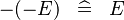 |
A | ||
| SIMP_MULTI_MINUS | 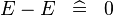 |
A | ||
| SIMP_SPECIAL_PROD_0 | 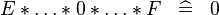 |
A | ||
| SIMP_SPECIAL_PROD_1 | 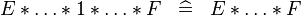 |
A | ||
| SIMP_SPECIAL_PROD_MINUS_EVEN | 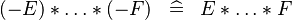 |
if an even number of  |
A | |
| SIMP_SPECIAL_PROD_MINUS_ODD | 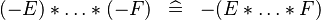 |
if an odd number of  |
A | |
| SIMP_LIT_MINUS | 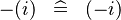 |
where  is a literal is a literal |
A | |
| SIMP_LIT_MINUS_MINUS | 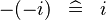 |
where  is a literal is a literal |
A | |
| SIMP_LIT_EQUAL | 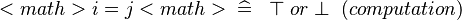 |
where  and and  are literals are literals |
A | |
| SIMP_LIT_LE | 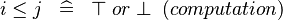 |
where  and and  are literals are literals |
A | |
| SIMP_LIT_LT | 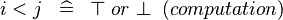 |
where  and and  are literals are literals |
A | |
| SIMP_LIT_GE | 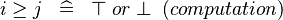 |
where  and and  are literals are literals |
A | |
| SIMP_LIT_GT | 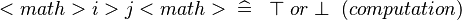 |
where  and and  are literals are literals |
A | |
| SIMP_DIV_MINUS | 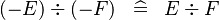 |
A | ||
| SIMP_SPECIAL_DIV_1 |  |
A | ||
| SIMP_SPECIAL_DIV_0 | 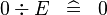 |
A | ||
| SIMP_SPECIAL_EXPN_1 | 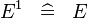 |
A | ||
| SIMP_SPECIAL_EXPN_0 | 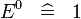 |
A | ||
| SIMP_MULTI_LE | 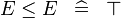 |
A | ||
| SIMP_MULTI_LT | 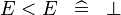 |
A | ||
| SIMP_MULTI_GE | 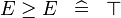 |
A | ||
| SIMP_MULTI_GT | 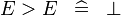 |
A | ||
| SIMP_MULTI_DIV | 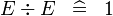 |
A | ||
| SIMP_MULTI_MOD | 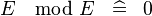 |
A | ||
| DISTRI_PROD_PLUS | 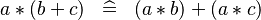 |
M | ||
| DISTRI_PROD_MINUS | 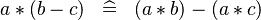 |
M | ||
| DERIV_LE_CARD | 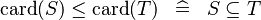 |
 and and  must be of the same type must be of the same type |
M | |
| DERIV_GE_CARD | 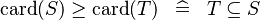 |
 and and  must be of the same type must be of the same type |
M | |
| DERIV_LT_CARD | 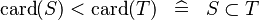 |
 and and  must be of the same type must be of the same type |
M | |
| DERIV_GT_CARD | 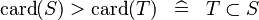 |
 and and  must be of the same type must be of the same type |
M | |
| DERIV_EQUAL_CARD | 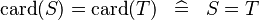 |
 and and  must be of the same type must be of the same type |
M |
Some rules are not yet implemented:
- SIMP_SPECIAL_KUNION, SIMP_SPECIAL_KUNION, SIMP_SPECIAL_KINTER, SIMP_SPECIAL_POW, SIMP_SPECIAL_POW1, SIMP_SPECIAL_CPROD_R, SIMP_SPECIAL_CPROD_L, SIMP_SPECIAL_COMPSET_BFALSE, SIMP_SPECIAL_COMPSET_BTRUE, SIMP_SPECIAL_EQUAL_COMPSET, SIMP_SPECIAL_OVERL, SIMP_SPECIAL_DOMRES_L, SIMP_SPECIAL_DOMRES_R, SIMP_SPECIAL_RANRES_R, SIMP_SPECIAL_RANRES_L, SIMP_SPECIAL_DOMSUB_L, SIMP_SPECIAL_DOMSUB_R, SIMP_SPECIAL_RANSUB_R, SIMP_SPECIAL_RANSUB_L, SIMP_SPECIAL_FCOMP, SIMP_SPECIAL_BCOMP, SIMP_SPECIAL_DPROD_R, SIMP_SPECIAL_DPROD_L, SIMP_SPECIAL_PPROD_R, SIMP_SPECIAL_PPROD_L, SIMP_SPECIAL_RELIMAGE_L, SIMP_SPECIAL_CONVERSE, SIMP_SPECIAL_ID, SIMP_SPECIAL_REL_R, SIMP_SPECIAL_REL_L, SIMP_SPECIAL_EQUAL_REL, SIMP_SPECIAL_EQUAL_RELDOM, SIMP_SPECIAL_PRJ1, SIMP_SPECIAL_PRJ2, SIMP_SPECIAL_LAMBDA, SIMP_SPECIAL_MOD_0, SIMP_SPECIAL_MOD_1, SIMP_SPECIAL_IN_NATURAL1, SIMP_SPECIAL_KBOOL_BTRUE, SIMP_SPECIAL_KBOOL_BFALSE, SIMP_SPECIAL_DIV_1, SIMP_SPECIAL_EQUAL_RELDOMRAN, SIMP_SPECIAL_FORALL_BTRUE, SIMP_SPECIAL_FORALL_BFALSE, SIMP_SPECIAL_EXIST_BTRUE, SIMP_SPECIAL_EXIST_BFALSE, SIMP_SPECIAL_SUBSET_R, SIMP_SPECIAL_SUBSET_L