Arithmetic Rewrite Rules
From Event-B
Rules that are marked with a * in the first column are implemented in the latest version of Rodin. Rules without a * are planned to be implemented in future versions. Other conventions used in these tables are described in The_Proving_Perspective_(Rodin_User_Manual)#Rewrite_Rules.
| Name | Rule | Side Condition | A/M | |
|---|---|---|---|---|
| * | SIMP_SPECIAL_MOD_0 |
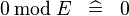 |
A | |
| * | SIMP_SPECIAL_MOD_1 |
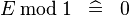 |
A | |
| * | SIMP_MIN_SING |
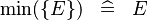 |
where  is a single expression is a single expression |
A |
| * | SIMP_MAX_SING |
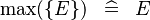 |
where  is a single expression is a single expression |
A |
| * | SIMP_MIN_NATURAL |
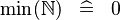 |
A | |
| * | SIMP_MIN_NATURAL1 |
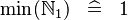 |
A | |
| * | SIMP_MIN_BUNION_SING |
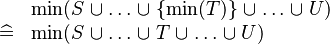 |
A | |
| * | SIMP_MAX_BUNION_SING |
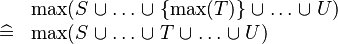 |
A | |
| * | SIMP_MIN_UPTO |
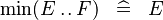 |
A | |
| * | SIMP_MAX_UPTO |
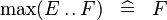 |
A | |
| * | SIMP_LIT_MIN |
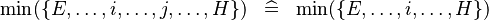 |
where  and and  are literals and are literals and 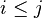 |
A |
| * | SIMP_LIT_MAX |
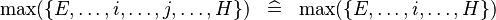 |
where  and and  are literals and are literals and 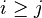 |
A |
| * | SIMP_SPECIAL_CARD |
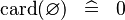 |
A | |
| * | SIMP_CARD_SING |
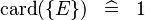 |
where  is a single expression is a single expression |
A |
| * | SIMP_SPECIAL_EQUAL_CARD |
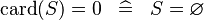 |
A | |
| * | SIMP_CARD_POW |
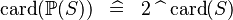 |
A | |
| * | SIMP_CARD_BUNION |
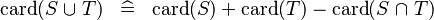 |
A | |
SIMP_CARD_SETMINUS |
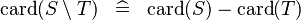 |
with hypotheses 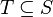 and either and either 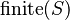 or or 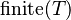 |
A | |
SIMP_CARD_SETMINUS_SETENUM |
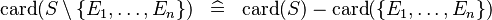 |
with hypotheses 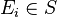 for all for all 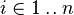 |
A | |
| * | SIMP_CARD_CONVERSE |
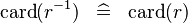 |
A | |
| * | SIMP_CARD_ID |
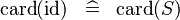 |
where 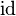 has type has type 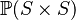 |
A |
| * | SIMP_CARD_ID_DOMRES |
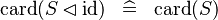 |
A | |
| * | SIMP_CARD_PRJ1 |
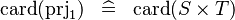 |
where 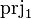 has type has type 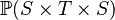 |
A |
| * | SIMP_CARD_PRJ2 |
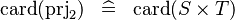 |
where 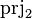 has type has type 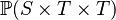 |
A |
| * | SIMP_CARD_PRJ1_DOMRES |
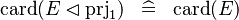 |
A | |
| * | SIMP_CARD_PRJ2_DOMRES |
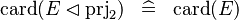 |
A | |
| * | SIMP_CARD_LAMBDA |
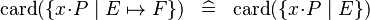 |
where  is a maplet combination of bound identifiers and expressions that are not bound by the comprehension set (i.e., is a maplet combination of bound identifiers and expressions that are not bound by the comprehension set (i.e.,  is syntactically injective) and all identifiers bound by the comprehension set that occur in is syntactically injective) and all identifiers bound by the comprehension set that occur in 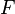 also occur in also occur in  |
A |
| * | SIMP_LIT_CARD_UPTO |
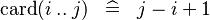 |
where  and and  are literals and are literals and 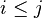 |
A |
SIMP_TYPE_CARD |
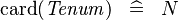 |
where 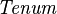 is a carrier set containing is a carrier set containing 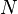 elements elements |
A | |
| * | SIMP_LIT_GE_CARD_1 |
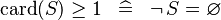 |
A | |
| * | SIMP_LIT_LE_CARD_1 |
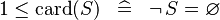 |
A | |
| * | SIMP_LIT_LE_CARD_0 |
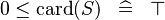 |
A | |
| * | SIMP_LIT_GE_CARD_0 |
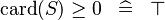 |
A | |
| * | SIMP_LIT_GT_CARD_0 |
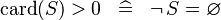 |
A | |
| * | SIMP_LIT_LT_CARD_0 |
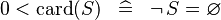 |
A | |
| * | SIMP_LIT_EQUAL_CARD_1 |
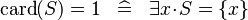 |
A | |
| * | SIMP_CARD_NATURAL |
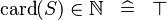 |
A | |
| * | SIMP_CARD_NATURAL1 |
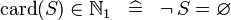 |
A | |
| * | SIMP_LIT_IN_NATURAL |
 |
where  is a non-negative literal is a non-negative literal |
A |
| * | SIMP_SPECIAL_IN_NATURAL1 |
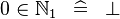 |
A | |
| * | SIMP_LIT_IN_NATURAL1 |
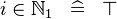 |
where  is a positive literal is a positive literal |
A |
| * | SIMP_LIT_UPTO |
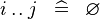 |
where  and and  are literals and are literals and 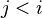 |
A |
| * | SIMP_LIT_IN_MINUS_NATURAL |
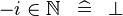 |
where  is a positive literal is a positive literal |
A |
| * | SIMP_LIT_IN_MINUS_NATURAL1 |
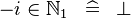 |
where  is a non-negative literal is a non-negative literal |
A |
| * | DEF_IN_NATURAL |
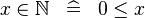 |
M | |
| * | DEF_IN_NATURAL1 |
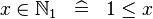 |
M | |
| * | SIMP_LIT_EQUAL_KBOOL_TRUE |
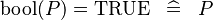 |
A | |
| * | SIMP_LIT_EQUAL_KBOOL_FALSE |
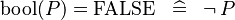 |
A | |
DEF_EQUAL_MIN |
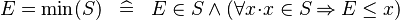 |
where  non free in non free in 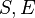 |
M | |
DEF_EQUAL_MAX |
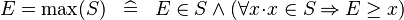 |
where  non free in non free in 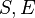 |
M | |
| * | SIMP_SPECIAL_PLUS |
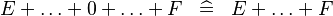 |
A | |
| * | SIMP_SPECIAL_MINUS_R |
 |
A | |
| * | SIMP_SPECIAL_MINUS_L |
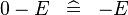 |
A | |
| * | SIMP_MINUS_MINUS |
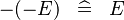 |
A | |
| * | SIMP_MINUS_UNMINUS |
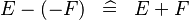 |
where 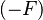 is a unary minus expression or a negative literal is a unary minus expression or a negative literal |
M |
| * | SIMP_MULTI_MINUS |
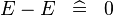 |
A | |
| * | SIMP_MULTI_MINUS_PLUS_L |
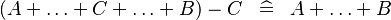 |
M | |
| * | SIMP_MULTI_MINUS_PLUS_R |
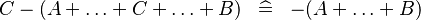 |
M | |
| * | SIMP_MULTI_MINUS_PLUS_PLUS |
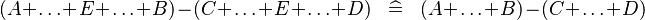 |
M | |
| * | SIMP_MULTI_PLUS_MINUS |
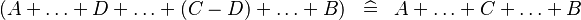 |
M | |
| * | SIMP_MULTI_ARITHREL_PLUS_PLUS |
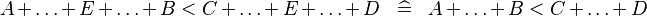 |
where the root relation (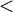 here) is one of here) is one of 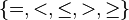 |
M |
| * | SIMP_MULTI_ARITHREL_PLUS_R |
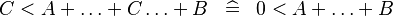 |
where the root relation (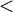 here) is one of here) is one of 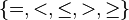 |
M |
| * | SIMP_MULTI_ARITHREL_PLUS_L |
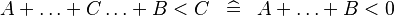 |
where the root relation (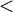 here) is one of here) is one of 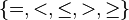 |
M |
| * | SIMP_MULTI_ARITHREL_MINUS_MINUS_R |
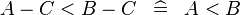 |
where the root relation (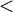 here) is one of here) is one of 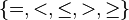 |
M |
| * | SIMP_MULTI_ARITHREL_MINUS_MINUS_L |
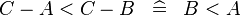 |
where the root relation (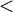 here) is one of here) is one of 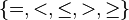 |
M |
| * | SIMP_SPECIAL_PROD_0 |
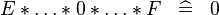 |
A | |
| * | SIMP_SPECIAL_PROD_1 |
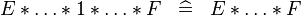 |
A | |
| * | SIMP_SPECIAL_PROD_MINUS_EVEN |
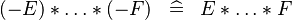 |
if an even number of  |
A |
| * | SIMP_SPECIAL_PROD_MINUS_ODD |
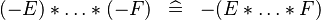 |
if an odd number of  |
A |
| * | SIMP_LIT_MINUS |
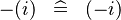 |
where  is a literal is a literal |
A |
| * | SIMP_LIT_EQUAL |
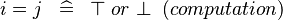 |
where  and and  are literals are literals |
A |
| * | SIMP_LIT_LE |
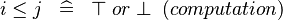 |
where  and and  are literals are literals |
A |
| * | SIMP_LIT_LT |
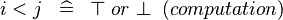 |
where  and and  are literals are literals |
A |
| * | SIMP_LIT_GE |
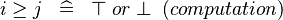 |
where  and and  are literals are literals |
A |
| * | SIMP_LIT_GT |
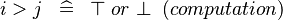 |
where  and and  are literals are literals |
A |
| * | SIMP_DIV_MINUS |
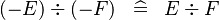 |
A | |
| * | SIMP_SPECIAL_DIV_1 |
 |
A | |
| * | SIMP_SPECIAL_DIV_0 |
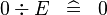 |
A | |
| * | SIMP_SPECIAL_EXPN_1_R |
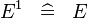 |
A | |
| * | SIMP_SPECIAL_EXPN_1_L |
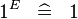 |
A | |
| * | SIMP_SPECIAL_EXPN_0 |
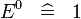 |
A | |
| * | SIMP_MULTI_LE |
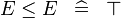 |
A | |
| * | SIMP_MULTI_LT |
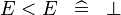 |
A | |
| * | SIMP_MULTI_GE |
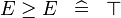 |
A | |
| * | SIMP_MULTI_GT |
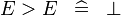 |
A | |
| * | SIMP_MULTI_DIV |
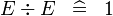 |
A | |
| * | SIMP_MULTI_DIV_PROD |
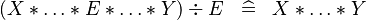 |
A | |
| * | SIMP_MULTI_MOD |
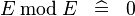 |
A | |
DISTRI_PROD_PLUS |
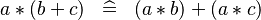 |
M | ||
DISTRI_PROD_MINUS |
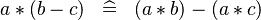 |
M | ||
DERIV_NOT_EQUAL |
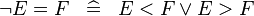 |
 and and 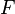 must be of Integer type must be of Integer type |
M |