Constrained Dynamic Parser: Difference between revisions
imported>Mathieu |
imported>Mathieu |
||
| Line 33: | Line 33: | ||
* sets : <math>\{a, b, c + e\}\;</math> or <math>\{ e \mid P\}\;</math> or <math>\{x,y . P \mid e\}\;</math> | * sets : <math>\{a, b, c + e\}\;</math> or <math>\{ e \mid P\}\;</math> or <math>\{x,y . P \mid e\}\;</math> | ||
We also want to define precisely | We also want to define precisely precedence and associativity between existing and new operators. | ||
=== Requirements exported by the dynamic feature === | === Requirements exported by the dynamic feature === | ||
Revision as of 14:06, 8 February 2010
This page describes the requirements for a generic parser for the Event-B Mathematical Language.
A first design proposal is also drafted.
Requirements
In order to be usable mathematical extensions require that the event-b mathematical language syntax can be extended by the final user.
The lexical analyser and the syntaxic parser thus have to be extensible in a simple enough way (from a user point of vue).
Requirements Exported by the Current Language Design
Operator Priority
- operator are defined by group,
- group of operator have a defined precedences,
- there may be precedences defined inside groups.
Operator Compatibility
- a compatibility table defines allowed associativities inside a group,
- a compatibility table defines allowed associativities between groups (it allows to forbid a syntaxic construction like
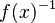 )
)
- nota: this requirement was added afterwards with consistency in mind.
Expected Extension Schemes
We do want to at least define operators of the following form :
- infix :
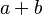 or
or 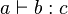
- prefix :
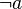
- postfix :
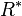
- closed :
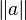
- parentheses sugar :
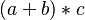
- functional postfix :
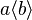
- functional prefix :
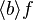
- lambda like :
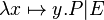
- Union like :
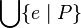 or
or 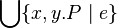
- sets :
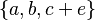 or
or 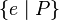 or
or 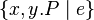
We also want to define precisely precedence and associativity between existing and new operators.
Requirements exported by the dynamic feature
- the precedence should not be enumerated, which would hinder extensibility, but defined by a relation, like: '+' < '*' and '*' < '**', ...
Limitations
TODO: explicit them
Design Alternatives
Three design alternatives where identified:
Make Existing Parser Extensible
The existing parser is a LL recursive descent parser generated by the Coco/R Compiler Generator, which makes extensive use of pre-computed lookahead, which makes it very difficult to be transformed in a parser witgh enough extensibility.
Parser Combinator
- on wikipedia. Some implementations are referenced here.
- with functionnal language Agda : Parsing Mixfix Operators
- This paper is interesting in its proposal of using an acyclic graph to define operator precedence.
- with functional language OPAL : How To Obtain Powerful Parsers That Are Elegant and Practical
Pratt Parser
Note that a pratt parser is essentially a parser for expressions (where expression parts are themselves expressions)... But it may be tweaked to limit the accepted sub-expressions or to enforce some non-expression parts inside an expression. More on that hereafter.
Some Existing Extensible Languages
- Katahdin, and the associated paper A Programming Language Where the Syntax and Semantics Are Mutable at Runtime which describes the language and its implementation (in C#).
- XMF whose implementation seems not be describes in details.
- XLR: Extensible Language and Runtime, which looks like a pratt parser according to the sources.
 whose implementation seems not be describes in details (but source code is available).
whose implementation seems not be describes in details (but source code is available).
Design Proposal
The chosen design is based on Pratt parser and is explained hereafter.
Main Concepts
- symbol
- a symbol is a lexem (finite,
 , ...)or a lexem class (number, identifier) known by the parser.
, ...)or a lexem class (number, identifier) known by the parser.
- group
- each symbol belongs to one and only one group (binary relation, assignment substitution,...).
- Groups are used to ease the definition of a hierarchy between operators in order to ease the definition of precedence and compatibility.
- symbol compatibility
- a relation telling if inside a group two symbol are compatibles.
- Two symbol are compatibles is they can be parsed without parentheses (see Event-B Mathematical Language for more on compatibility).
- group compatibility
- a relation telling if two groups are compatibles.
- Two symbol of different groups are said compatibles if their group are compatibles.
- symbol associativity
- a relation which gives the associative precedence of symbols inside a given group.
- group associativity
- a relation which gives the associative precedence of groups.
- Two symbol of different groups have a relative precedence given by the associative precedence of their groups.
- generic parser
- the parser which is defined.
- This parser may be called recursively (an infix expression being build upon a left and right sub-expression) and is often the default parser used when building the AST associated with a symbol.
- specific parser
- some specific parser, predefined as helper functions to build specific AST.
- nonterminal
- A nonterminal is a set of symbol. Nonterminals are used for acceptance or rejection of the AST produced by a parser on a sub-formula.
- nonterminals may be defined by mean of symbols, groups or other nonterminals.
Proposed User Interface
The hereafter proposition does not preclude the final UI from taќing other (more user friendly) form). But the concepts should probably stay the same
We propose that the user will be able to create several predefined type of symbols (new types may certainly be further added by mean of eclipse extension points). When defining a symbol, the user can choose the parser used to parse the sub-expressions (default to generic parser, but a specific parser may be used) and can enforce the form of the resulting parsed sub-expression in terms of their AST root type.
Predefined Symbol Builders
The proposed predefined symbol builders are:
- infix
- For example predicate conjunction which expects two predicates for left and right parts may be defined by
infix("∧", gid="(logic pred)", expected_nonterm=["predicate", "predicate"]), saying that '∧' is an operator belonging to the logic predicate group which accept a predicate on left and right. - As another example, substitution :∣ of group '(infix subst)' which expect one ident list for left term and and a predicate for the right one may be defined by
infix(":∣", "(infix subst)", expected_nonterm=["ident_list", "predicate"])
- prefix
prefix("¬", "(not pred)", expected_nonterm=["predicate"])
- atomic
atomic("⊤", "(atomic pred)")
- prefix closed
- used to build prefix symbol which must be followed by enclosing symbol(brackets, parentheses,..). For example finite may be defined by:
prefix_closed("finite", "(", ")","(atomic pred)", expected_nonterm=["expression"])
- postfix;
postfix("∼", gid="(unary relation)", expected_nonterm=["expression"])
- quantified
quantified("∀", "·", expected_nonterm=["predicate"]
- lambda like
lambda_like("λ", "·", u"∣", gid="(quantification)", expected_nonterm=["ident list", "predicate", "expression"])
- quantified union like
Union_like("⋃", "·", "∣", gid="(quantification)")
- closed sugar
- use for parentheses added to enforce associativity:
closed_sugar("(", ")")
- functional postfix
functional_postfix("(", ")", gid="(functional)", expected_nonterm=["expression", "expression"])
Some right associative versions of those symbol builders may also be supplied (infix_right, or a specific parameter right associative parameter may also be provided to the infix symbol builder).
TODO: Definition and use of nonterminals'
Predefined Specific Parser
- expression lists
- ident lists
- maplet tree (for lambda)
Defining Compatibility and Precedences
Inside a group, compatibility may be defined like:
g = group["(binop)"]
g.add_many_compatibility(
[ ("∪", "∪"),
("∩", "∩"),
("∩", "∖"),
("∩", "▷"),
("∩", "⩥"),
("∘", "∘"),
(";", ";"),
(";", "▷"),
(";", "⩥"),
("", ""),
("◁", "∩"),
("◁", "∖"),
("◁", ";"),
("◁", "⊗"),
("◁", "▷"),
("◁", "⩥"),
("⩥", "∩"),
("⩥", "∖"),
("⩥", ";"),
("⩥", "⊗"),
("⩥", "▷"),
("⩥", "⩥"),
("×", "×"), ]
which defines the compatibility table for expression binary operator as defined in Event-B Mathematical Language.
Inside a group, precedence may be defined like:
g = group["(arithmetic)"]
g.add_many_precedence(
[ ("^", "÷"),
("^", "∗"),
("^", "+"),
("^", "−"),
("^", "mod"),
("+", "∗"),
("−", "∗"),
("+", "÷"),
("−", "÷"),
("+", "mod"),
("−", "mod"), ] )
which defines ^ as having the least precedence amongst the operators of the expression arithmetic group.
Similarly, precedences and compatibilities between groups may be defined :
group_precedence.add(("(binop)", "(interval)"))
group_precedence.add(("(interval)", "(arithmetic)"))
group_precedence.add(("(arithmetic)", "(unary relation)"))
group_precedence.add(("(unary relation)", "(bound unary)"))
group_precedence.add(( "(bound unary)", "(bool)"))
group_compatibility.add_all( [ "(binop)", "(interval)", (arithmetic)", "(unary relation)", "(unary relation)", "(bound unary)",....])
Some Difficulties
Some difficulties appear when trying to implement an Event-B parser with the preceding scheme:
- A symbol may be declared by several different builders (think of unary and infix minus for example).
- Pratt parsers are able to cope with a symbol appearing either at the beginning of an expression or inside an expression (see led and nud hereafter). For example, unary minus and infix minus can be both defined by the proposed scheme. However, in their default form, pratt parser failed in parsing symbol like '{' which appears at the beginning of extension sets, comprehension sets and quantified sets.
- SOLUTION #1: The existing Event-B parser uses an infinite lookahead to determine which one of those three sets is actually being parsed.
- This solution hinders the extensibility of the parser, because the addition of a symbol requires to modify the lookahead.
- However, such an issue may be bypassed, at least in a first version, in enforcing some usage rules. Thus, a new symbol contributed by an extension but used in the lookahead may be rejected as in invalid symbol.
- SOLUTION #2: Implementing a backtracking parser.
- More precisely, it means that the parsing is attempted on every alternative (for example, on the three types of sets parser: extension, comprehension, and quantified). The parsing is successful if and only if one of these attempts lead to a result (i.e., it is a failure if several attempts or none lead to a result). All the error are collected and returned to the user in case of no match.
- It is a good solution provided that we use memorisation to alleviate the cost of parsing formulas that require heavy backtracking.
- Some binary infix operators are in fact parsed as n-ary operators (with more than 2 childrens if possible).
- An attribute is required to specify if an operator shall be flattened (i.e., parsed as an n-ary operator) or not. It is indeed impossible to "deduce" this information (e.g., the minus operator, which is left associative and self-compatible, shall not be flattened).
- The flattenning should then be done by the parser associated to every symbol.
- The returned parsing errors shall be meaningful for users (e.g., the "Missing parenthesis" message may help to solve the problem when the "Invalid expression" message is too imprecise)
- TODO: how does it impact actual design?.
- Defining a grammar or a grammar extension is not an easy job, even with those simple mechanisms.
- It would certainly be a good idea to implement a user interface to test the grammar, so that an extension designer has a way to ensure that he agrees with the parser on the semantic of his extension (or at least on the AST obtained by using it). For example, the representation of the syntax tree returned by Formula.getSyntaxTree could be compared to an expected entered string.
Core Algorithm
Rough description
The algorithm is based on a table, associating a SymbolParser for each known operator (or lexem class). The MainParser then constructs the AST by using the led or nud parser instance attached to each symbol, taking into account symbol innformation such as group and precedence for constructing the resulting AST.
Each led or nud parser instance may in turn make recursive calls to either the standard MainParser or to ad-hoc parsers. The choice of the subparsers used is given when the SymbolParser is created.
TODO: to be completes?
Main Objects
- KnownSymbols
- a table associating a SymbolParser for each known symbol.
- Tokenizer tokenizer
- which provides the SymbolParser associated to the next lexem of the formula being parsed.
- TODO: shall be a singleton ? Define how is it use by Parser object
- SymbolParser
- a Parser for a specific symbol. It should at least have the following attributes:
- Array<LedParser> led_parsersfor parsing the expression associated to the symbolidwhen it appears in the middle of an expression (left denotation)
- Array<NudParser> nud_parsersfor parsing the expression associated to the symbolidwhen it appears at the beginning of an expression (null denotation)
- String idwhich is the lexem concerned by those parsers.
- String giddesigning the group to which theidsymbol belongs to.
- Array<LedParser>
- and the following members:
AST led(AST left): which should iterate with backtracking over led_parsers.led()AST nud(AST left): which should iterate with backtracking over nud_parsers.nud()
- Note that parsers in led (respectively nud) will be tried one after another (with backtracking to the original state in between). If several of them succeed, an error is returned to the user, else the AST generated by the only one succeeding is returned. If none succeeded, an error is raised.
- LedOrNudParser
- An abstract parser, that may be used by the MainParser, which should have the following attributes
- Array<Parser> subparsers: an array of subparsers used by theparsemethod. They defaults toMainParser, but may be set to specific parsers.
- Array<Parser>
- LedParser
- An abstract parser which inherits from LedOrNudParser and provides the following method:
AST led(AST left): which given an already parsed left AST will construct the AST associated to the lexem being parsed, by analysing the part of the formula on its right.
- NudParser
- An abstract parser which inherits from LedOrNudParser and provides the following method:
AST nud(): which build an AST associated to the lexem being parsed, by analysing the part of the formula on its right.
- Parser
- An abstract class of a recursive descent like parser which is used by the led or nud functions to build parts from AST. It may be instanciated by the MainParser or by any specific parser (used to parse list of identifier, or other structures taht do not fit well in the general Pratt parser schema ...). It has the following attribute:
- Nonterminals Set: set of nonterminals that are expected to be return by the parse function. If the root of the AST returned by the parse function is not one of the expected nonterminals, then an error is raised stating which non-terminals were expected, and which one was found.
- and the following method:
AST parse(): this method should consume tokens provided by the tokenizer and returns an AST. It may use severalsubparsers.
- MainParser
- This class inherits from Parser and its parsefunction implements the core of the pratt algorithm.
- Without taking into account backtracking, the algorithm reads:
def parse(reckognized_token, has_right_associativity=False):
global token
t = token # t is the processed symbol
token = tokenizer.next() # token is the next symbol
left = t.nud() # a new expression is being parsed (null denotation : nothing on the left)
while has_less_priority(reckognized_token, token, has_right_associativity):
t = token
token = next_token() # if precedence allows it, we parse next expression
left = t.led(left) # has being left expression of current symbol (left denotation)
return left
- The parsing of a new expression is then initiated by:
token = tokenizer.next()
ast = MainParser.parse(KnownSymbols["(eof)"])
- identListParser
- inherits from Parser. Its parsefunction implements the parsing of an ident list (like
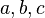 ).
).
- identMapletListParser
- inherits from Parser . Its parsefunction implements the parsing of a maplet list as used in lambda expression (like
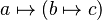 ).
).
- expressionListParser
- inherits from Parser . Its parsefunction implements a list of expression as used in the extension set expression.
TODO: section being worked on
- infixParser
- inherits from Parser. Its parsefunction is a led parser and implements something like (pseudocode):
parse(AST left):
ast = new AST()
ast.first = left
verify_expected_group(ast.first, this.expected_non_terminals[0])
ast.second = this.parsers[0].parse(ast, is_right_associative=False)
verify_expected_group(ast.second, this.expected_non_terminals[1])
return ast
Open Questions
How does the user specify the expected AST?
- Some examples in the existing parser:
- Bound identifiers are converted to de Bruijn indexes while constructing the AST. Is this desirable ? How does the user specify that identifier are bound or not ?
Sample Implementation
A prototype as been developed in Python to quickly try different solutions.
The development tree of the python prototype is available at http://bitbucket.org/matclab/eventb_pratt_parser/ with the default branch implementing a rather functionnal approach and the object branch being a first try to a more object based implementation.
Tests
- Regression tests. The tests of the existing parser shall succeed when applied to the generic parser.
- New tests.