Constrained Dynamic Parser
This page describes the requirements for a generic parser for the Event-B Mathematical Language. It will also draft a first design proposal.
Requirements
In order to be usable mathematical extensions require the event-b mathematical language syntax to be extensible by the final user.
Thus, the lexical analyser and the syntaxic parser have to be extensible in a simple enough way (from a user point of vue).
Requirements Exported by the Current Language Design
Operator Priority
- operator are defined by group,
- group of operator have a defined precedences,
- there may be precedences defined inside groups.
Operator Compatibility
- a compatibility table defines allowed associativities inside a group,
- a compatibility table defines allowed associativities between groups (it allows to forbid a syntaxic construction like
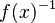
- nota: this requirement was added afterwards with consistency in mind.
Expected Extension Schemes
We do want to at least define operators of the following form :
- infix :
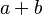 or
or 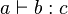
- prefix :
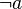
- postfix :
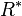
- closed :
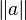
- parentheses sugar :
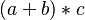
- functional postfix :
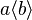
- functional prefix :
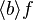
- lambda like :
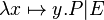
- Union like :
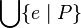 or
or 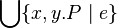
- sets :
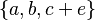 or
or 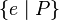 or
or 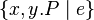
We also like to define precisely precedences and associativity between existing and new operators.
Requirements exported by the dynamic feature
- the precedence should not be enumerated but defined by a relation, like: '+' < '*' and '*' < '**', ...
Limitations
Design Alternatives
Make Existing Parser Extensible
The existing parser is a LL recursive descent parser generated by the Coco/R Compiler Generator, which makes extensive use of pre-computed lookahead, which makes it very difficult to be transformed in a sufficiently enough generic parser.
Parser Combinator
- on wikipedia. Some implementations are referenced here.
- with functionnal language Agda : Parsing Mixfix Operators
- This paper is interesting in its proposal of using an acyclic graph to define operator precedence.
- with functional language OPAL : How To Obtain Powerful Parsers That Are Elegant and Practical
Pratt Parser
Note that a pratt' parser is essentially a parser for expressions (where expression parts are themselves expressions)... But it may be tweaked to limit the accepted sub-expressions or to enforce some non-expression parts inside an expression. More on that hereafter.
Some Existing Extensible Languages
- Katahdin, and the associated paper A Programming Language Where the Syntax and Semantics Are Mutable at Runtime which describes the language and its implementation (in C#).
- XMF whose implementation seems not be describes in details.
- XLR: Extensible Language and Runtime, which looks like a pratt parser according to the sources.
 whose implementation seems not be describes in details (but sources availables).
whose implementation seems not be describes in details (but sources availables).
Design Proposal
Main Concepts
- symbol
- a symbol is a lexem known by the parser.
- group
- each symbol belongs to one and only one group.
- symbol compatibility
- a relation telling if inside a group two symbol are compatibles.
- Two symbol are compatibles is they can be parsed without parentheses (see Event-B Mathematical Language for more on compatibility).
- group compatibility
- a relation telling if two groups are compatibles.
- Two symbol of different groups are said compatibles if their group are compatibles.
- symbol associativity
- a relation which gives the associative precedence of symbols inside a given group.
- group associativity
- a relation which gives the associative precedence of groups.
- Two symbol of different groups have a relative precedence given by the associative precedence of their groups.
- generic parser
- the parser which is defined.
- This parser may be called recursively (an infix expression being build upon a left and right sub-expression) and is often the default parser used when building the AST associated with a symbol.
- specific parser
- some specific parser, predefined as helper functions to build specific AST.
- Some example of specific parser are the one used to parse and build list of identifiers (for quantified predicates), mapplets lists (for lambda), and so one...
Proposed User Interface
The hereafter proposition does not preclude the final UI to take other (more user friendly forms). But the concepts should probably stay the same
We propose that the user will be able to create several predefined type of symbols (new types may certainly be further added by mean of eclipse extension points). When defining a symbol, the user can choose the parser used to parse the sub-expressions (default to generic parser, but a specific parser may be used) and can enforce the form of the resulting parsed sub-expression in terms of their AST root type.
Predefined Symbol Builders
The proposed predefined symbol builders are:
- infix
- For example predicate conjunction which expect two predicates for left and right parts may be defined by
infix("∧", gid="(logic pred)", expected_nonterm=["predicate", "predicate"]) - As another example, substitution ≔ of group '(infix subst)' which expect two ident list for left and right expressions may be defined by
infix(symbol="≔", gid="(infix subst)", parsers=["ident_list", "ident_list"], expected_nonterm=["ident_list", "ident_list"]) - prefix
prefix("¬", "(not pred)", expected_nonterm=["predicate"])- atomic
atomic("⊤", "(atomic pred)")- prefix closed
- used to build prefix symbol which must be followed by enclosing symbol(brackets, parentheses,..). For example finite may be defined by:
prefix_closed("finite", "(", ")","(atomic pred)", expected_nonterm=["expression"]) - postfix:
postfix("∼", gid="(unary relation)", expected_nonterm=["expression"]) - quantified
quantified("∀", "·", expected_nonterm=["predicate"]- lambda like
lambda_like("λ", "·", u"∣", gid="(quantification)", expected_nonterm=["ident list", "predicate", "expression"])- quantified union like
Union_like("⋃", "·", "∣", gid="(quantification)")- closed sugar
- Like parentheses added to enforce associativity:
closed_sugar("(", ")") - functional postfix
functional_postfix("(", ")", gid="(functional)", expected_nonterm=["expression", "expression"])
Some right associative versions of those symbol builders may also be supplied (infix_right, or a specific parameter right associative parameter may also be provided to the infix symbol builder).
Predefined Specific Parser
- expression lists
- ident lists
- maplet tree (for lambda)
Defining Compatibility and Precedences
Inside a group, compatibility may be defined like:
g = group["(binop)"]
g.add_many_compatibility(
[ ("∪", "∪"),
("∩", "∩"),
("∩", u"∖"),
("∩", "▷"),
("∩", "⩥"),
("∘", "∘"),
(";", ";"),
(";", "▷"),
(";", "⩥"),
("", ""),
("◁", "∩"),
("◁", "∖"),
("◁", ";"),
("◁", "⊗"),
("◁", "▷"),
("◁", "⩥"),
("⩥", "∩"),
("⩥", "∖"),
("⩥", ";"),
("⩥", "⊗"),
("⩥", "▷"),
("⩥", "⩥"),
("×", "×"), ]
which defines the compatibility table for expression binary operator as defined in Event-B Mathematical Language.
Inside a group, precedence may be defined like:
g = group["(arithmetic)"]
g.add_many_precedence(
[ ("^", "÷"),
("^", "∗"),
("^", "+"),
("^", "−"),
("^", "mod"),
("+", "∗"),
("−", "∗"),
("+", "÷"),
("−", "÷"),
("+", "mod"),
("−", "mod"), ] )
which defines ^ as having the least precedence amongst the operators of the expression arithmetic group.
Similarly, precedences and compatibilities between groups may be defined :
group_precedence.add(("(binop)", "(interval)"))
group_precedence.add(("(interval)", "(arithmetic)"))
group_precedence.add(("(arithmetic)", "(unary relation)"))
group_precedence.add(("(unary relation)", "(bound unary)"))
group_precedence.add(( "(bound unary)", "(bool)"))
group_compatibility.add_all( [ "(binop)", "(interval)", (arithmetic)", "(unary relation)", "(unary relation)", "(bound unary)",....])
Some Difficulties
- different builders for the same symbol
- common prefixes TODO: backtracking + memoisation
- Grammar testing TODO: should be include in the user interface: the user shall provide tests with its extensions to ensure that he agree with the parser on the semantic of its extension
Core Algorithm
Sample Implementation
A prototype as been developed in Python to quickly try different solutions.
The development tree is available at http://bitbucket.org/matclab/eventb_pratt_parser/