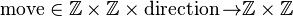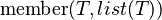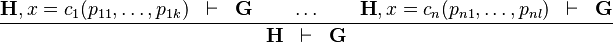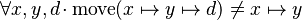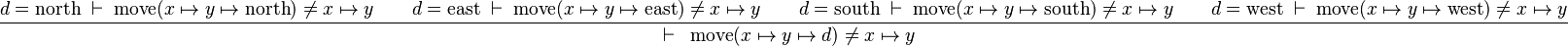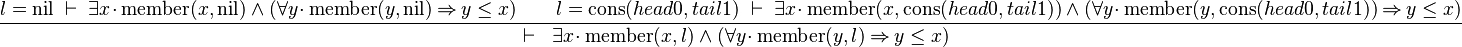Datatype Rules
Datatype rules may seem a bit difficult to understand at first sight. Here are a few examples intended to make them clearer.
Datatypes used
The rules will be applied to the following datatypes:
Directions:
direction ::=
north
| east
| south
| west
Let us have a function
first two arguments are a start position, third is a direction, result is the end position.
Lists:
list(T) ::=
nil
| cons( head : T, tail : list(T) )
Let us have a predicate
meaning that the first argument is a member of the list.
Trees:
tree(T) ::= empty | node( left : tree(T), value : T, right : tree(T) )
Let us have a function
defining the height of a tree
Distinct Case
The rule states
Application to directions
Starting from goal
we can free variables x,y,d then apply Distinct Case:
The resulting proof step is
further simplifications depend on the existence of rules about move and the various directions.
Application to lists
Starting from goal
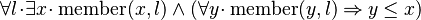
we can free variable l then apply Distinct Case on it:
The left antecedent shows that the case of the nil list has been forgotten when writing the theorem.
Application to trees
TODO
!l,v,r. t = node(l,v,r) => height(l) < height(t)
Induction
TODO