Constrained Dynamic Lexer
This page describes the requirements for a parameterizable lexical analyser (i.e. lexer) for the Event-B Mathematical Language.
A first design proposal is also drafted.
Requirements
In order to be usable, mathematical extensions require that the Event-B mathematical language syntax can be extended by the final user.
The lexical analyser and the syntactic parser thus have to be extensible in a simple enough way (from a user point of view).
Requirements Exported by the Current Language Design
- lexems and tokens to be used are known at lexer's instantiation.
Requirements Exported by the Dynamic Feature
- lexems and their corresponding tokens are collected from Event-B Mathematical Language's set of keywords and from mathematical extensions,
- a given lexem corresponds to a unique token.
Design Proposal
The keywords defining the Event-B Mathematical Language, or the mathematical extensions used to parameterize the lexer are converted into a set of directed graphs. Each node represents a state in lexem recognition, and each transition represents a choice in the symbol to continue the recognition with. An array of symbols to be recognized, can be associated with a node in order to group a sequence of transitions where no choice is needed to be done. This is an optimisation to prevent a cumbersome creation of node objects.
When a lexem is scanned, the lexer tries to find an entry node in the set of graphs, that corresponds to its beginning (i.e. its first character). Traversing the graph, the lexer finds out if the current lexem is actually a keyword or not.
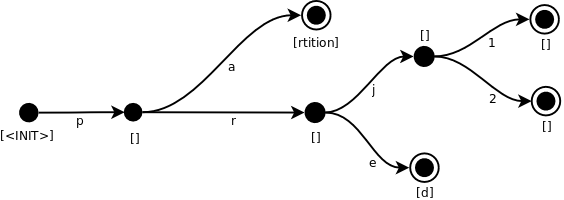
Here is a figure describing the recognition graph associated for a lexem beginning with the letter p (where configuration keywords beginning with the letter "p" are : "partition", "prj1", "prj2" and "pred".
Same behaviour
Identifiers
The generic parser will hold the current construction of identifiers. In the current version of the Event-B Mathematical Language, identifiers are defined against this Unicode syntactical rule :
<identifier> := <identifier_start> (<identifier_start> | <identifier_extend>)*
and implemented with the following rules : <identifier_start> can be any character valid under the terms of Character.isJavaIdentifierStart(char ch) except :
- '$' which indicates the beginning of a predicate variable's name,
- 'λ' (\u0033)
<identifier_extend> can be any character valid under the terms of Character.isJavaIdentifierPart(char ch) except :
- '$'
- 'λ' (\u0033)
and possibly completed by a "'".
Open Questions
There are currently 4 types of lexems : identifiers, numbers, predicate variables, and keywords.
Is it valuable to complement those 4 types of lexems including comments that could this way be placed anywhere?