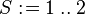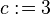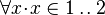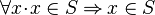Difference between revisions of "Generic Instantiation"
imported>Laurent |
imported>Laurent (Full rewrite of the issues adding plenty of details) |
||
| Line 7: | Line 7: | ||
However, besides the declared axioms in the development to be extended there are two ''implicit'' axioms for every carrier set <math>S</math>: | However, besides the declared axioms in the development to be extended there are two ''implicit'' axioms for every carrier set <math>S</math>: | ||
| + | # ''non-emptiness'': <math> S \neq \emptyset</math> | ||
| + | # ''maximality'': <math>\forall x \qdot x \in S</math> | ||
| − | + | There are two ways to tackle these implicit axioms: | |
| + | # Restrict instantiation of carrier sets to type expressions | ||
| + | # Allow for general instantiation with some additions | ||
| − | + | In the first option, a carrier set can only be instantiated with an expression denoting a type. This can be syntactically verified. The advantage of this solution is that the two axioms are then verified implicitly, because any type expression satisfies these two axioms. Moreover, as type expressions are the only expressions that can satisfy both axioms, this is the only option which is viable if we are to consider that these two axioms must be fulfilled by an instantiation. | |
| − | + | The second option consists in relaxing the conditions for generic instantiation by dropping the second implicit axiom (maximality). Then, a carrier set could be instantiated by any expression that denotes a non-empty set. However, dropping maximality does not come without strong consequences, because it is the justification for the type inference used in event-B: | |
| − | + | For instance, les us consider a context declaring a carrier set <math>S</math>, a constant <math>c</math> and the ''theorem'' <math>c\in S</math>. This context does not contain any axiom, but <math>c</math> is typed by inference in the theorem. This context can easily be proved as the theorem can be deduced from typing. Then, this context could be instantiated by taking: | |
| + | :<math>S\bcmeq 1\upto2</math> | ||
| + | :<math>c\bcmeq 3</math> | ||
| + | which would bring the instantiated ''theorem'' <math>3\in 1\upto2</math> which is obviously false. | ||
| − | + | Consequently, if we drop the maximality axiom, we have to generate additional proof obligations for showing that every instantiation of a constant belongs to the instantiation of its type. | |
| − | + | However, there are more general issues. If a context contains theorem | |
| + | :<math>\forall x\qdot x\in S</math> | ||
| + | then using the same instantiation for <math>S</math> as above, one would obtain the instantiated ''theorem'' | ||
| + | :<math>\forall x\qdot x\in 1\upto2</math> | ||
| + | which is also wrong. To mitigate this issue, all quantifications occurring in the initial context would need to be complemented by adding typing predicates for every quantified variables. For instance, the theorem above would be rewritten as | ||
| + | :<math>\forall x\qdot x\in S \limp x\in S</math> | ||
| + | where we have added a typing predicate on the left-hand side of implication. | ||
| + | |||
| + | Similar issues happen for generic operators such as identity, where types need again to be explicited before instantiation (e.g., <math>\id</math> would become <math>S\domres \id</math>). | ||
| + | |||
| + | All this can be implemented in a tool, but it can be deceptive to users as the instantiated context can become quite different from the original context (when a lot of typing predicates and expressions have been added automatically by the instantiation plug-in). | ||
| + | |||
| + | In retrospect, the first option (instantiation only by type expressions) does not introduce any loss of generality. If one has a context with a carrier set <math>S</math> and wants to instantiate this carrier set with an arbitrary expression, it is always possible to modify the context by introducing an additional constant <math>s</math> and replace all (implicit or explicit) occurrences of <math>S</math> by <math>s</math>. This would be done in a manner similar to all the adjustments proposed for the second option above. However, all these adjustments would be made under the control of proof, rather than performed by a tool. Moreover, the user would have the opportunity to see exactly the consequences of replacing the carrier set by the constant and adjusting his model consequently. Finally, the advantage of the first option is that it keeps instantiation very simple, both for implementation in tools and for explaining how it works to prospective users. | ||
[[Category:Design proposal]] | [[Category:Design proposal]] | ||
Revision as of 10:51, 6 April 2010
The initial proposal from Southampton is as follows. File:Proposal generic instantiation rodin.pdf.
Issues: Instantiation of Carrier Sets
Currently, the proposal mentions that the carrier sets can be instantiated with any set expressions (which contains existing carrier sets and constants).
However, besides the declared axioms in the development to be extended there are two implicit axioms for every carrier set  :
:
- non-emptiness:
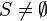
- maximality:
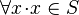
There are two ways to tackle these implicit axioms:
- Restrict instantiation of carrier sets to type expressions
- Allow for general instantiation with some additions
In the first option, a carrier set can only be instantiated with an expression denoting a type. This can be syntactically verified. The advantage of this solution is that the two axioms are then verified implicitly, because any type expression satisfies these two axioms. Moreover, as type expressions are the only expressions that can satisfy both axioms, this is the only option which is viable if we are to consider that these two axioms must be fulfilled by an instantiation.
The second option consists in relaxing the conditions for generic instantiation by dropping the second implicit axiom (maximality). Then, a carrier set could be instantiated by any expression that denotes a non-empty set. However, dropping maximality does not come without strong consequences, because it is the justification for the type inference used in event-B:
For instance, les us consider a context declaring a carrier set  , a constant
, a constant  and the theorem
and the theorem 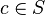 . This context does not contain any axiom, but
. This context does not contain any axiom, but  is typed by inference in the theorem. This context can easily be proved as the theorem can be deduced from typing. Then, this context could be instantiated by taking:
is typed by inference in the theorem. This context can easily be proved as the theorem can be deduced from typing. Then, this context could be instantiated by taking:
which would bring the instantiated theorem 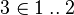 which is obviously false.
which is obviously false.
Consequently, if we drop the maximality axiom, we have to generate additional proof obligations for showing that every instantiation of a constant belongs to the instantiation of its type.
However, there are more general issues. If a context contains theorem
then using the same instantiation for  as above, one would obtain the instantiated theorem
as above, one would obtain the instantiated theorem
which is also wrong. To mitigate this issue, all quantifications occurring in the initial context would need to be complemented by adding typing predicates for every quantified variables. For instance, the theorem above would be rewritten as
where we have added a typing predicate on the left-hand side of implication.
Similar issues happen for generic operators such as identity, where types need again to be explicited before instantiation (e.g., 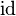 would become
would become 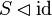 ).
).
All this can be implemented in a tool, but it can be deceptive to users as the instantiated context can become quite different from the original context (when a lot of typing predicates and expressions have been added automatically by the instantiation plug-in).
In retrospect, the first option (instantiation only by type expressions) does not introduce any loss of generality. If one has a context with a carrier set  and wants to instantiate this carrier set with an arbitrary expression, it is always possible to modify the context by introducing an additional constant
and wants to instantiate this carrier set with an arbitrary expression, it is always possible to modify the context by introducing an additional constant  and replace all (implicit or explicit) occurrences of
and replace all (implicit or explicit) occurrences of  by
by  . This would be done in a manner similar to all the adjustments proposed for the second option above. However, all these adjustments would be made under the control of proof, rather than performed by a tool. Moreover, the user would have the opportunity to see exactly the consequences of replacing the carrier set by the constant and adjusting his model consequently. Finally, the advantage of the first option is that it keeps instantiation very simple, both for implementation in tools and for explaining how it works to prospective users.
. This would be done in a manner similar to all the adjustments proposed for the second option above. However, all these adjustments would be made under the control of proof, rather than performed by a tool. Moreover, the user would have the opportunity to see exactly the consequences of replacing the carrier set by the constant and adjusting his model consequently. Finally, the advantage of the first option is that it keeps instantiation very simple, both for implementation in tools and for explaining how it works to prospective users.