Mathematical Language Evolution Design: Difference between revisions
imported>Nicolas |
imported>Nicolas |
||
| Line 23: | Line 23: | ||
The new parser has a version attribute. Depending on the version, formulas are parsed differently. Thus, the KPARTITION node is a regular identifier if version is V1. It is accepted as a keyword only from version V2. | The new parser has a version attribute. Depending on the version, formulas are parsed differently. Thus, the KPARTITION node is a regular identifier if version is V1. It is accepted as a keyword only from version V2. | ||
Concerning identity and projections, they are recognized as non-generic with V1 and generic with V2. | Concerning identity and projections, they are recognized as non-generic with V1 and generic with V2. | ||
The following table summarizes how tokens are processed depending on the | The following table summarizes how tokens are processed depending on the language version: | ||
| Line 29: | Line 29: | ||
|+ Token Recognition | |+ Token Recognition | ||
! scope=col | | ! scope=col | | ||
! scope=col | | ! scope=col |Language V1 | ||
! scope=col | | ! scope=col |Language V2 | ||
|- | |- | ||
! scope=row |"partition" | ! scope=row |"partition" | ||
| Line 51: | Line 51: | ||
==== Parsing ==== | ==== Parsing ==== | ||
FormulaFactory has new {{method|parse()}} methods with a | FormulaFactory has new {{method|parse()}} methods with a language version argument. Existing methods default to the first version ({{class|LanguageVersion.V1}}), while becoming deprecated. | ||
Thus, one now has to know, before parsing a formula, the version of the language it has been written with. | Thus, one now has to know, before parsing a formula, the version of the language it has been written with. | ||
It also provides methods to [[#Upgrade|upgrade]] to the new language version. | It also provides methods to [[#Upgrade|upgrade]] to the new language version. | ||
Revision as of 13:49, 17 April 2009
Introduction
This document describes the modifications that occur to the Event-B mathematical language from the developer point of view. The old language will still be recognized, in order to provide backward compatibility.
These changes are described from a user point of view in Changes to the Mathematical Language of Event-B.
Abstract Syntax Tree
Deprecated nodes (becoming atomic expressions):
- KPRJ1
- KPRJ2
- KID
New nodes:
- KPARTITION that represents the new partition predicate (multiple predicate)
- KPRJ1_GEN that represents the generic atomic version of the first projection
- KPRJ2_GEN that represents the generic atomic version of the second projection
- KID_GEN that represents the generic atomic version of the identity
Parser Changes
The new parser has a version attribute. Depending on the version, formulas are parsed differently. Thus, the KPARTITION node is a regular identifier if version is V1. It is accepted as a keyword only from version V2. Concerning identity and projections, they are recognized as non-generic with V1 and generic with V2. The following table summarizes how tokens are processed depending on the language version:
| Language V1 | Language V2 | |
|---|---|---|
| "partition" | IDENT | KPARTITION |
| "id" | KID | KID_GEN |
| "prj1" | KPRJ1 | KPRJ1_GEN |
| "prj2" | KPRJ2 | KPRJ2_GEN |
Parsing
FormulaFactory has new parse() methods with a language version argument. Existing methods default to the first version (LanguageVersion.V1), while becoming deprecated. Thus, one now has to know, before parsing a formula, the version of the language it has been written with. It also provides methods to upgrade to the new language version.
Multiple Predicates / Partition
A new predicate class is introduced: MultiplePredicate, in which the partition predicate is implemented. A MultiplePredicate is a predicate that applies to a list of one or more expressions. In a partition, all expressions must have the same type, that is the type of the partitioned set (first child).
Associativity
Newly non associative relational set operators now require parentheses around their operands for parsing to succeed. This is managed directly by the parser. Unparsing also requires those parentheses, so the BinaryExpression.toString() method has been changed accordingly.
Visitors
Partition, identity and projections also entail new visitor methods, as follows:
IVisitor has 6 more methods:
- enterKPARTITION(MultiplePredicate)
- continueKPARTITION(MultiplePredicate)
- exitKPARTITION(MultiplePredicate)
- visitKID_GEN(AtomicExpression)
- visitKPRJ1_GEN(AtomicExpression)
- visitKPRJ2_GEN(AtomicExpression)
ISimpleVisitor has 1 more method:
- visitMultiplePredicate(MultiplePredicate)
Thus, implementors of those interfaces are required to implemented new methods, while subclassers of DefaultVisitor and DefaultSimpleVisitor should consider whether or not to override them.
Sequent Prover
TODO
Upgrade
Formulas written with version V1 will need upgrading to version V2. However, most of the V1 formulas will be exactly the same with V2. A formula needs ugrading if:
- it contains one of {KPRJ1, KPRJ2, KID}
- it contains a non parenthesised sequence of relational set operators
In these cases an upgrade procedure will be applied to the formula using a IFormulaRewriter, to rewrite KPRJ1, KPRJ2, KID expressions into their generic equivalent (see Changes to the Mathematical Language of Event-B#Generic Identity and Projections).
Formatting
Ideally, upgrading a formula would preserve its previous formatting (spaces, tabs, new lines). But this turns out being quite tricky. Indeed, it prevents from simply rewriting the formula then applying a toString(), as this would totally forget and override any formatting. Thus, we would have to write directly into the original string. Firstly find the source locations where changes will occur, then patching the formula with the new expression versions at those source locations.
But that leads to more complexity when we come to consider formulas that contain
- recursive relational set operators (that recursively shift source locations)
- binary operators with higher priorities nearby (that mindlessly absorb a member of the rewritten expression)
Let's look at the following formula:
A straight rewriting would proceed as follows:
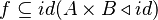 which already is false (requires parentheses)
which already is false (requires parentheses)
Then, with the appropriate shift of the source location to replace the first 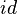 operator:
operator:
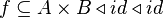 which is even worse
which is even worse
This suggests putting parentheses around rewritten expressions. But they would sometimes be superfluous, which brings us to distinguish cases where they are needed and cases where they are not, depending on the priority of the operators nearby.
Considering this is going quite far, a simpler upgrade method is applied:
- if the formula does not use deprecated expressions, nor lacks parentheses around relational set operators, it is left unchanged, preserving the formatting
- it it does, it is rewritten and any previous formatting is overridden