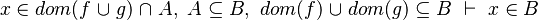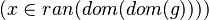Membership in Goal: Difference between revisions
imported>Laurent |
imported>Laurent |
||
| Line 68: | Line 68: | ||
#*<math>x\in ran(f),\quad f\subseteq A\cprod B\quad\vdash\quad x\in B</math> | #*<math>x\in ran(f),\quad f\subseteq A\cprod B\quad\vdash\quad x\in B</math> | ||
By using these inclusions | By using these inclusions the tactic tries to find a path among the recovered hypotheses. Every one of them should only be used once, avoiding possible infinite loop <math>\left(A\subseteq B,\; B\subseteq A\right)</math>. | ||
Since Rodin 3.0, the path search is delegated to the [http://www.sat4j.org Sat4j] solver. The problem encoding to SAT is done by representing each inclusion of the form <math>A\subseteq B</math> into the clause <math>\{\lnot x\in A,\; x\in B\}</math> and feeding the solver with all clauses that derive from the hypotheses and the negation of the goal. As soon as the solver reports the problem as unsatisfiable, the tactic obtains an unsat core and traces it back to the corresponding hypotheses. | |||
== Reasoner == | == Reasoner == | ||
Revision as of 17:13, 30 August 2013
Objective
This page describes the design of the reasoner MembershipGoal and its associated tactic MembershipGoalTac.
This reasoner discharges sequents whose goal denotes a membership which can be inferred from hypotheses, such as the following:
Analysis
Usually, such sequents are proved by the external provers PP or ML. But, these provers have several drawbacks :
- They do not report needed hypotheses, so that a conservative choice is made to depend on all hypotheses.
- They take substantial time to prove them (even with the basic example given above, the difference in time execution is noticeable).
- If there are too many hypotheses, or if the expression of the
 or the intermediate sets
or the intermediate sets  is too complicated, they may get lost into details and not discharge.
is too complicated, they may get lost into details and not discharge.
This is particularly true when in the set expressions of each side of relations are not equal, such as in:
Such a reasoner thus increases the rate of automated proof, faster and with fewer needed hypotheses which makes proof rules more legible and proof replay less sensitive to modifications of the models.
Design Decision
Tactic
This part explains how the tactic (MembershipGoalTac) associated to the reasoner MembershipGoal is working.
Goal
The tactic (as the reasoner) should works only on goals such as :
For examples :
In the last example, the reasoner will not try to prove that  belongs to
belongs to 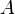 and
and 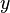 belongs to
belongs to 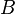 , but that the maplet
, but that the maplet 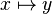 belongs to the Cartesian product
belongs to the Cartesian product 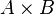 .
.
Hypotheses
Now we have to find hypotheses leading to discharge the sequent. To do so, the tactic recovers two kinds of hypotheses :
- the ones related to the left member of the goal
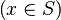 (this is the start point):
(this is the start point):
- the ones denoting inclusion (all but the ones matching the description of the first point) :
Then, it will search a link between those hypotheses so that the sequent can be discharged.
Find a path
Now that we recovered all the hypotheses that could be useful for the reasoner, it remains to find a path among the hypotheses leading to discharge the sequent. Depending on the relations on each side of the inclusion, we will act differently. 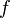 always represent an expression (may be a domain, a range, etc.).
always represent an expression (may be a domain, a range, etc.).
- The following sequent is provable because
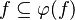 .
.
- The following sequent is provable because
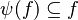 .
.
- By keeping the notation
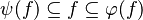 we also deduce that :
we also deduce that :
- For some relations, positions are needed to be known to continue to find hypotheses, but it is not always necessary.
By using these inclusions the tactic tries to find a path among the recovered hypotheses. Every one of them should only be used once, avoiding possible infinite loop 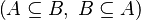 .
.
Since Rodin 3.0, the path search is delegated to the Sat4j solver. The problem encoding to SAT is done by representing each inclusion of the form 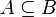 into the clause
into the clause 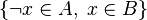 and feeding the solver with all clauses that derive from the hypotheses and the negation of the goal. As soon as the solver reports the problem as unsatisfiable, the tactic obtains an unsat core and traces it back to the corresponding hypotheses.
and feeding the solver with all clauses that derive from the hypotheses and the negation of the goal. As soon as the solver reports the problem as unsatisfiable, the tactic obtains an unsat core and traces it back to the corresponding hypotheses.
Reasoner
This part describe how the reasoner MembershipGoal works.
Goal
First, it checks that the goal matches the description made in the part tactic : 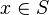 . Thus, we record the member x as well as the set S
. Thus, we record the member x as well as the set S
Input
Then, it checks that the input is a hypothesesReasonerInput (an input with an array of predicates). Every given predicates must be contained in the sequent. Only one must be related to the goal's member so that there are no ambiguity. All the other ones must denote inclusion.
Find a path
With the same reasoning as for the tactic, we try to find a path leading to discharge the goal.
Trusted Base
At that point, the reasoner performs the same jobs as the tactic which is quite complicated. That poses one problem : it is hard to proof the reasoner is safe (only doing what it was meant to, not discharging sequent that cannot be proofed). Because reasoners are in the trusted base, we should be absolutely sure of what they perform. How to validate the found path ?
As we know, the reasoner condense several inferences rules in only one proof rule. To validate the found path, we have to validate every single inference rule. To achieve it, we use the class created in that purpose : Rules. Each rules contain one predicate and an array of rules (its antecedents). When the path is searched, the rule corresponding is created. When the path is found, we test if the predicate of the rule is equal to the goal. If not, it means the path found was incorrect, so the reasoner fails, else the sequent is discharged.
Example of rules :
Implementation
This section explain how the tactic has bee implemented.
Positions
As it was said, we may sometimes need the position. It is represented by an array of integer. Here are the possible values the array contains (atomic positions) :
- kdom : it corresponds to the domain.
- kran : it corresponds to the domain.
- converse : it corresponds to the child of an inverse
For example, the following expressions at the given positions are equivalent.
Some combinations of atomic positions are equivalent. In order to simplify comparison between positions, they are normalized :
Goal
A pair (expression ; position) 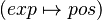 is said to be contained in the goal if and only if exp is contained in the goal, and if the position matched of exp in the goal is equal to pos. For examples, let's see the annexe
is said to be contained in the goal if and only if exp is contained in the goal, and if the position matched of exp in the goal is equal to pos. For examples, let's see the annexe
Hypotheses
As explained in the design decision part, there are two kinds of hypotheses which are recovered. But when hypotheses related to the left member of the goal 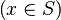 are stored, the position of x is also record. Then, if there is an hypothesis such as
are stored, the position of x is also record. Then, if there is an hypothesis such as 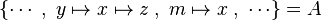 , then this hypothesis is mapped to the positions
, then this hypothesis is mapped to the positions ![\left\{\left[kdom,~kran\right],~\left[kran\right]\right\}](/images/math/9/d/e/9dec9494124653aa1d260b86b3ec63b6.png) .
.
Find a path
Let's consider that following sequent : 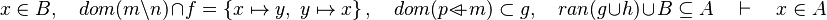 .
.
- From the goal we get two informations : the member which is x as well as the set we try to prove it belongs to which is A.
- By knowing x we recover hypothesis giving informations about it. In our study case, from the hypothesis
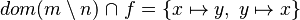 we infer that x belong to
we infer that x belong to 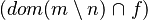 at those possible positions
at those possible positions ![\left[\;\left[kran\right],~\left[kdom\right]\;\right]](/images/math/9/b/2/9b2525d0fd7457b76a35133adceee724.png)
- Tactic : record all these informations
![\left\{x\in B\mapsto B\mapsto\left[\;\right]\;,\;\left(dom(m\setminus n)\binter f = \left\{x\mapsto y,\;y\mapsto x\right\}\right)\mapsto\left(dom(m\setminus n)\binter f\right)\mapsto\left[\;\left[kran\right],\;\left[kdom\right]\;\right]\right\}](/images/math/e/5/a/e5abaaa101875821c51c4917383a2e2b.png)
- Reasoner : We consider that the tactic will found the most complicated path. For each positions, we make the associated rule, which give in our example
![\left\{dom(m\setminus n)\binter f\;\mapsto\;\left[kdom\right]\;\mapsto\;x\in dom(dom(m\setminus n)\binter f),~~~dom(m\setminus n)\binter f\;\mapsto\;\left[kran\right]\;\mapsto\;x\in ran(dom(m\setminus n)\binter f)\right\}](/images/math/2/5/0/250ef6badd8a27ccb2384192e2e025e2.png) .
.
- Tactic : record all these informations
- Now, that we have a set to start the search of a path
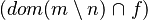 , we get all the expression containing it :
, we get all the expression containing it : 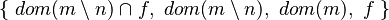 . As we don't want to have expression such as dom(...), we modify the position.
. As we don't want to have expression such as dom(...), we modify the position.
- Tactic : Here, there are only the mapping between the positions and the expression :
![\left\{\;dom(m\setminus n)\binter f\;\mapsto\;\left[kran\right],~~~f\;\mapsto\;\left[kran\right],~~~m\;\mapsto\;\left[kdom,\;kran\right],~~~m\setminus n\;\mapsto\;\left[kdom,\;kran\right]\;\right\}](/images/math/3/0/0/300a6c7324bede364c6c42ab3271d55a.png)
- Reasoner : we generate the rule corresponding to the computed sets :
![\left\{~\cdots~m\;\mapsto\;\left[kdom,\;kran\right]\;\mapsto\;x\in ran(dom(m))~\cdots~\right\}](/images/math/c/9/a/c9ab65378fe9d515022dadaca34518f4.png)
- Tactic : Here, there are only the mapping between the positions and the expression :
- We test if one of these pair is contained in the goal. If so, we move to the step 5. But it clearly appears that it is not the case. So, we try to find hypotheses among the one denoting inclusion which are related to that pair. We clearly see that the expression
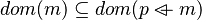 . Actually, we search every expressions containing m using that mapping
. Actually, we search every expressions containing m using that mapping ![m\;\mapsto\;\left[kdom,\;kran\right]](/images/math/2/a/2/2a280627ba059dc53f9a4fd35b81df92.png) . From
. From 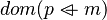 we can say that only the domain of m is contained in it. Then it ensures this position is part of the position of m in which x belongs to. If so we remove that position and obtain a new mapping
we can say that only the domain of m is contained in it. Then it ensures this position is part of the position of m in which x belongs to. If so we remove that position and obtain a new mapping ![g\;\mapsto\;\left[kran\right]](/images/math/9/2/2/922bfb302681bb3fdc5feff12800793c.png) (more details here) and we step back to 3 with that new pair.
(more details here) and we step back to 3 with that new pair.
- Reasoner : the rule corresponding is generated
![g\;\mapsto\;\left[kran\right]\;\mapsto\;x\in ran(g)](/images/math/d/d/5/dd5ada678438e1004ba17491170c0480.png)
- Reasoner : the rule corresponding is generated
- We find a path, the works is done.
- Tactic : If a path has been found, then we call the reasoner with all the used predicates as input.
- Reasoner :At the end, we check that the generated rule is equal to the goal. If so, the sequent is discharged. Else, a failure is returned.
We see that the tactic may not find the most simple path to discharge the sequent. Moreover, there are some cases where the tactic is able to find a path but the reasoner is unable to prove it due to a weakness in the rules (see all the untreated cases). Example :
Depending on whether the tactic returns 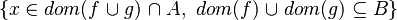 or
or 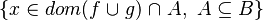 , the reasoner will fail or succeed. To prevent such hazardous behavior, re-writing should be proceeded.
, the reasoner will fail or succeed. To prevent such hazardous behavior, re-writing should be proceeded.
Annexe
| Predicate | Position of g matched | Inferred predicate | Position in h |
|---|---|---|---|
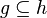
|
![\left[\;\right]](/images/math/e/9/f/e9f10aab7f1d1853e48a35759bd4f82d.png)
|
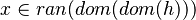
|
![\left[kdom,\;kdom,\;kran\right]](/images/math/0/0/3/0032a4d210e56c2156e2fa7f095d327c.png)
|
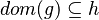
|
![\left[kdom\right]](/images/math/c/5/c/c5cc72861c15c538518490cf1fba92c0.png)
|
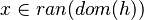
|
![\left[kdom,\;kran\right]](/images/math/6/2/0/62001a9bcbd65cb3b1750ce33603bf0c.png)
|
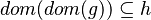
|
![\left[kdom,\;kdom\right]](/images/math/f/0/9/f0991db6c29e2977b1960f8688f54679.png)
|
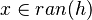
|
![\left[kran\right]](/images/math/2/7/d/27d789b29d7b2de957695f972e650324.png)
|
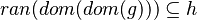
|
![\left[kdom,\;kdom,\;kran\right]](/images/math/0/0/3/0032a4d210e56c2156e2fa7f095d327c.png)
|
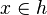
|
![\left[~\right]](/images/math/f/e/f/feff10f9f32d8789edb2406245e6e9e7.png)
|
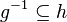
|
![\left[conv\right]](/images/math/5/7/e/57e603c01f75a7af4129181a47495a28.png)
|

|
![\left[kran,\;kdom,\;kran\right]](/images/math/f/f/8/ff8dfc3aa821851437f8a69126b6dfaf.png)
|
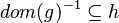
|
![\left[kdom,\;conv\right]](/images/math/2/1/c/21cd5a26b8199756c58988c0f81aae2c.png)
|
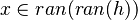
|
![\left[kran,\;kran\right]](/images/math/4/7/d/47d7fe3e912e1f25dd1eadbea6cac656.png)
|
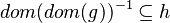
|
![\left[kdom,\;kdom,\;conv\right]](/images/math/4/b/2/4b27b84739e32f89b51ee6a7b55a25ec.png)
|
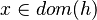
|
![\left[kdom\right]](/images/math/c/5/c/c5cc72861c15c538518490cf1fba92c0.png)
|
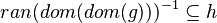
|
![\left[kdom,\;kdom,\;kran,\;conv\right]](/images/math/d/9/c/d9cf597b4a78e4bde0a945167e38779e.png)
|
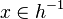
|
![\left[conv\right]](/images/math/5/7/e/57e603c01f75a7af4129181a47495a28.png)
|
In the case a converse appears at the end of the position of g matched, it is removed, then, we test if the position is part of the position. If so, it is removed and converse is added at the beginning of the array (which is automatically normalized).
Untreated cases
Some cases are not treated. Further enhancement may be provided for some.
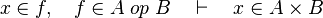
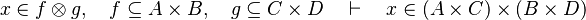 as well as all the possibles re-writing.
as well as all the possibles re-writing.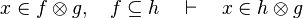
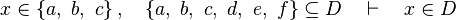
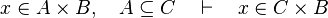
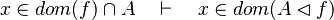
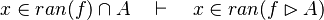
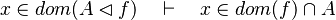
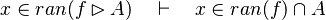
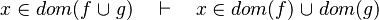
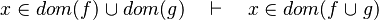
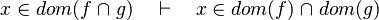
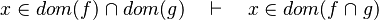
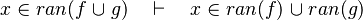
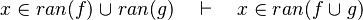
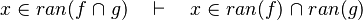
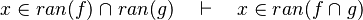
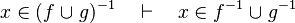
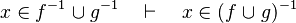
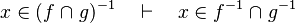
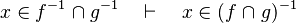
- the last 12 examples fails because the Rules have some weakness. This show that some re-writing should be performed.
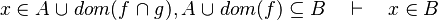
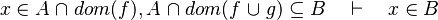
- the reason for the failure of the two last examples is that when union or intersection are compared, we should take all the expression containing each member, but we don't.
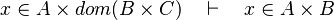
- it fails because when we get equivalent expression of the Cartesian product, we don't go further enough.
 where
where 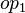 and
and 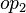 are ones of :
are ones of :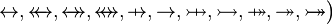
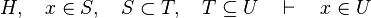
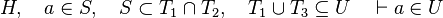
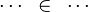
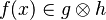
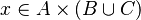
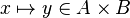
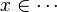
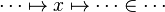
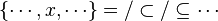
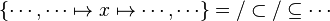
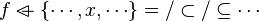

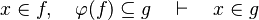

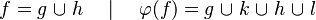
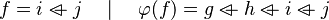
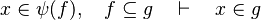

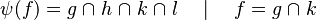
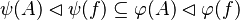
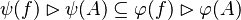
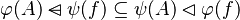
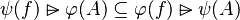
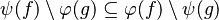
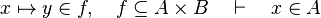
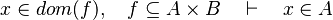
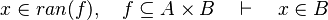
![name\;of\;the\;rule\quad\frac{predicate\;of\;first\;antecedent\cdots predicate\;of\;last\;antecedent}{consequent\;of\;that\;rule}\left[parameters\right]](/images/math/7/3/8/738ee7373b0e1a92b55d65082dd2382e.png)
![Hypothesis\quad\frac{}{predicate}\left[predicate\right]](/images/math/1/7/a/17abab213beec189eb50a58ce52ee038.png)
![IncludBunion\quad\frac{A\bunion B\bunion C\bunion D\subseteq Z}{B\bunion C\subseteq Z}\left[B,~C\right]](/images/math/0/9/e/09e97fc97bd903a468796b8bb6f18662.png)
![Composition\quad\frac{x\in A,~A\subseteq B}{x\in B}\left[~\right]](/images/math/9/8/3/983d29f85e3242414072ee357ca55f1b.png)
![\left[A\cprod B\right]_{pos\;=\;kdom} = A](/images/math/5/c/9/5c9188384893a5f785386fd9be5f5211.png)
![\left[x\mapsto y\right]_{pos\;=\;kdom} = x](/images/math/2/0/2/202d5f1c44ca4d283d912b36a0363bdb.png)
![\left[g\right]_{pos\;=\;kdom} = dom(g)](/images/math/9/e/8/9e8243fbfbf64a5fbf4dd9c86a803249.png)
![\left[A\cprod B\right]_{pos\;=\;kran} = B](/images/math/5/1/e/51e9dde2c7714a18994bfd88133abaff.png)
![\left[x\mapsto y\right]_{pos\;=\;kran} = y](/images/math/a/f/9/af9a897a8826985891b874f9b9909e12.png)
![\left[g\right]_{pos\;=\;kran} = ran(g)](/images/math/7/f/1/7f1b4c4c2ce799142d20e081fab53cff.png)
![\left[f^{-1}\right]_{pos\;=\;converse}=f](/images/math/f/6/d/f6d099908d10e496857d491b0ee6bca9.png)
![\left[A\cprod B\right]_{pos\;=\;converse} = B\cprod A](/images/math/5/5/8/5580559f9c30df0338362d5a49c66335.png)
![\left[ran(dom(g))\right]_{pos\;=\;\left[\right]} = \left[dom(g)\right]_{pos\;=\;\left[kran\right]} = \left[g\right]_{pos\;=\;\left[kdom,\; kran\right]}](/images/math/1/5/7/1578bdb9722f70811943df524818d8d8.png)
![ran(f^{-1}) = dom(f)\quad\limp\quad \left[f\right]_{pos \;=\; \left[converse,~kran\right]} = \left[f\right]_{pos\;=\;\left[kdom\right]}](/images/math/9/a/b/9ab2c57a971be9093b74331cfdf365f2.png)
![dom(f^{-1}) = ran(f)\quad\limp\quad \left[f\right]_{pos \;=\; \left[converse,~kdom\right]} = \left[f\right]_{pos\;=\;\left[kran\right]}](/images/math/d/1/4/d145100f50452d20541cbc2113d8a9c4.png)
![\left(f^{-1}\right)^{-1} = f\quad\limp\quad \left[f\right]_{pos \;=\; \left[converse,~converse\right]} = \left[f\right]_{pos\;=\;\left[~\right]}](/images/math/f/f/2/ff2fe24f0d2d75efe4839f2d2bfe2130.png)