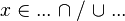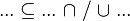Membership in Goal: Difference between revisions
imported>Josselin add inference rules |
imported>Nicolas |
||
| Line 116: | Line 116: | ||
For instance, from the hypothesis "<math> f \ovl \{ x \mapsto y \} \in A \rel B </math>" the reasoner derives the predicates <math>x \in A</math> and <math>x \in dom(A \cprod B)</math>. | For instance, from the hypothesis "<math> f \ovl \{ x \mapsto y \} \in A \rel B </math>" the reasoner derives the predicates <math>x \in A</math> and <math>x \in dom(A \cprod B)</math>. | ||
Afterwards, the reasoner has to encode the new predicates in SAT clauses. For this purpose, it converts all new hypotheses in SAT proposition by extracting all set contained into the predicate. And then, | Afterwards, the reasoner has to encode the new predicates in SAT clauses. For this purpose, it converts all new hypotheses in SAT proposition by extracting all set contained into the predicate. And then, it encodes the proposition SAT in Dimacs CNF format. Finally, the clauses encoded are inserted one by one into the SAT problem until the solver reports the problem as unsatisfiable in order to obtain a minimal solution to the SAT core. | ||
{| class="wikitable" style="text-align:center; width:80%;" | {| class="wikitable" style="text-align:center; width:80%;" | ||
Revision as of 13:47, 5 June 2014
Objective
This page describes the design of the reasoner MembershipGoal and its associated tactic MembershipGoalTac.
This reasoner discharges sequents whose goal denotes a membership which can be inferred from hypotheses, such as the following:
Analysis
Usually, such sequents are proved by the external provers PP or ML. But, these provers have several drawbacks :
- They do not report needed hypotheses, so that a conservative choice is made to depend on all hypotheses.
- They take substantial time to prove them (even with the basic example given above, the difference in time execution is noticeable).
- If there are too many hypotheses, or if the expression of the
 or the intermediate sets
or the intermediate sets  is too complicated, they may get lost into details and not discharge.
is too complicated, they may get lost into details and not discharge.
This is particularly true when in the set expressions of each side of relations are not equal, such as in:
Such a reasoner thus increases the rate of automated proof, faster and with fewer needed hypotheses which makes proof rules more legible and proof replay less sensitive to modifications of the models.
Design Decision
Tactic
This part explains how the tactic (MembershipGoalTac) associated to the reasoner MembershipGoal is working.
Goal
The tactic (as the reasoner) works only on goals of the form :
For example:
In the last example, the reasoner will not try to prove that  belongs to
belongs to 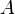 and
and 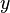 belongs to
belongs to 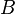 , but that the maplet
, but that the maplet 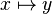 belongs to the Cartesian product
belongs to the Cartesian product 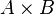 .
.
Hypotheses
Now we have to find hypotheses leading to discharge the sequent. To do so, the tactic looks for two kinds of hypothesis :
- the ones related to the left member of the goal
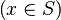 (which will be used as a starting point):
(which will be used as a starting point):
- the ones denoting inclusion (which will be used to find a path from a starting point to the goal) :
Then, it will search a link between these hypotheses so that the sequent can be discharged.
Find a path
Now that we have found all the hypotheses that could be useful to the reasoner, it remains to find a path among these hypotheses leading to discharge the sequent. Depending on the relations on each side of the inclusion, we will act differently. 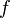 always denotes an expression (it may be a domain, a range, etc.).
always denotes an expression (it may be a domain, a range, etc.).
- The following sequent is provable because
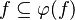 .
.
- The following sequent is provable because
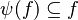 .
.
- By keeping the notation
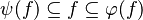 we also deduce that :
we also deduce that :
- For some relations, positions are needed to be known to continue to find hypotheses, but it is not always necessary.
By using these inclusions the tactic tries to find a path among the recovered hypotheses. Every one of them should only be used once, avoiding possible infinite loop 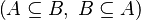 .
.
Since Rodin 3.0, the path search is delegated to the Sat4j solver. The problem encoding to SAT is done by representing each inclusion of the form 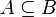 into the clause
into the clause 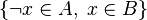 and feeding the solver with all clauses that derive from the hypotheses and the negation of the goal. As soon as the solver reports the problem as unsatisfiable, the tactic obtains an unsat core and traces it back to the corresponding hypotheses.
and feeding the solver with all clauses that derive from the hypotheses and the negation of the goal. As soon as the solver reports the problem as unsatisfiable, the tactic obtains an unsat core and traces it back to the corresponding hypotheses.
Reasoner
This part describe how the reasoner MembershipGoal works.
Goal
First, it checks that the goal matches the description made in the part tactic : 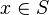 . Thus, we record the member x as well as the set S
. Thus, we record the member x as well as the set S
Input
Then, it checks that the input is a hypothesesReasonerInput (an input with an array of predicates). Every given predicates must be a hypothesis of the sequent. Only one must be a membership with the same member as the goal so that there are no ambiguity. All the other ones must denote set inclusion or equality.
Find a path
With the same reasoning as for the tactic, we try to find a path leading to discharge the goal.
Trusted Base
At that point, the reasoner performs the same jobs as the tactic which is quite complicated. That poses one problem : it is hard to prove the reasoner to be sound (only doing what it was meant to, not discharging sequents that cannot be proved). Because the reasoner is in the trusted base, we should be absolutely sure of what it performs. How to validate the found path ?
As we know, the reasoner condense several inferences rules in only one proof rule. To validate the found path, we have to validate every single inference rule. To achieve it, we create, internally to the reasoner, a small proof tree built from internal proof rules (implemented in class Rules). Each rule contains one predicate and an array of rules (its antecedents). When the path is searched, the corresponding rule is created. When the path is found, we check that the predicate of the root rule is the same as the goal. If not, it means the found path was incorrect, so the reasoner fails, else the sequent is discharged.
Example of rules :
Implementation
This section explains how the reasoner has been implemented.
Hypotheses
From the hypotheses, the reasoner derives new hypotheses leading to discharge the sequent. As explained in the design decision part, there are two kinds of hypotheses which are recovered (membership and inclusion). So, we developped two extractors which extract useful predicates from the hypotheses with these inference rules. For each new hypothesis a rationale is built, this rationale contains the derived predicate and a rule used as a justification.
Find a path
Let's consider the following sequent : 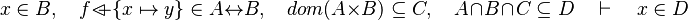
From the hypotheses and the negation of the goal the reasoner derives new predicates.
For instance, from the hypothesis "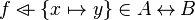 " the reasoner derives the predicates
" the reasoner derives the predicates 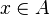 and
and 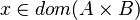 .
.
Afterwards, the reasoner has to encode the new predicates in SAT clauses. For this purpose, it converts all new hypotheses in SAT proposition by extracting all set contained into the predicate. And then, it encodes the proposition SAT in Dimacs CNF format. Finally, the clauses encoded are inserted one by one into the SAT problem until the solver reports the problem as unsatisfiable in order to obtain a minimal solution to the SAT core.
| Sequent | SAT proposition | Dimacs CNF format |
|---|---|---|
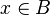
|
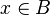
|
|
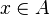
|
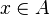
|
|
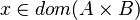
|
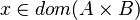
|
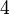
|
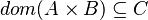
|
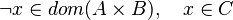
|
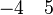
|
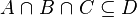
|
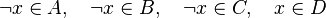
|
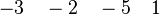
|
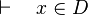
|
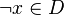
|
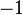
|
Afterwards, the reasoner traces each clause of the explanation returned by the SAT solver back to the corresponding hypotheses. However, the clauses returned by the SAT solver are sorted by their insertion order in the SAT core. So the reasoner reorders them by using topological sorting. Specifically, when the reasoner adds a rationale, we are guaranteed that all rationales on which it depends are already in the list.
Now, the reasoner has to build the path, for each hypothesis into the list, a new rationale is built and saved into an array at the index of the list. If the hypothesis denotes a membership, the rationale is directly saved into the array. Else the reasoner retrieves from the array all rationales on which it depends and then from these rationales it builds a new rationale and saves it into the array.
However, the path building is unidirectionnal, it works with a sat problem with clauses containing whith at most one positive literal. Indeed, the current version can't find a path with hypotheses in the following form :
An example of found path in a tree form:
Comp:├── Hyp:
└── Inter:
├── Hyp:
├── Hyp:
└── Comp:
├── Hyp:
└── Hyp:
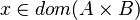
Finally, the reasoner checks that the generated rule from the rationale is equal to the goal. If so, the sequent is discharged. Else, a failure is returned
Inference rules
Here the rules that should be implemented for the reasoner MembershipGoal.
| Inference Rule | Side condition | Implemented |
|---|---|---|
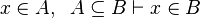
|
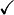
| |
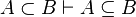
|
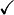
| |
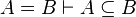
|
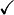
| |
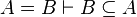
|
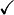
| |
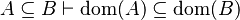
|
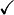
| |
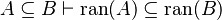
|
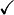
| |
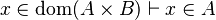
|
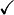
| |
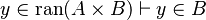
|
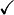
| |
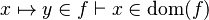
|
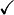
| |
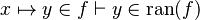
|
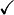
| |

|
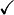
| |
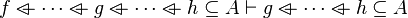
|
| |
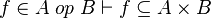
|
where 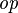 is one of is one of 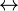 , , 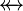 , , 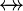 , , 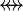 , , 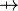 , , 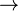 , , 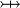 , , 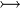 , , 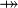 , , 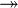 , , 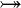
|
|
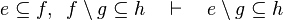
|
||
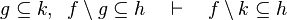
|
||
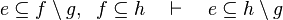
|
||
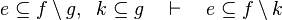
|
||
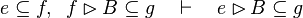
|
||
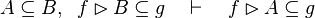
|
||
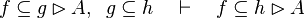
|
||
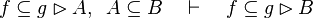
|
||
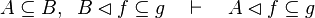
|
||
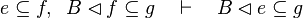
|
||
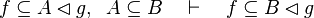
|
||
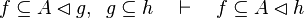
|
||
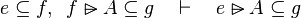
|
||
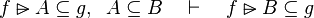
|
||
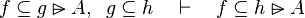
|
||
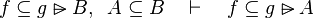
|
||
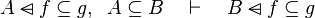
|
||
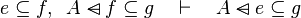
|
||
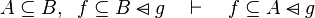
|
||
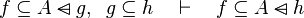
|
||
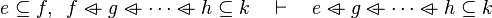
|
||
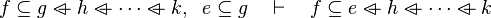
|
||
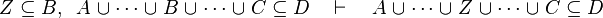
|
||
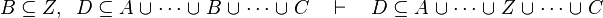
|
||
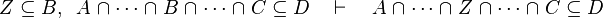
|
||
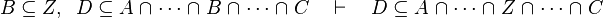
|
||
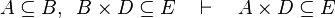
|
||
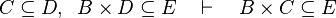
|
||
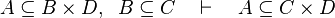
|
||
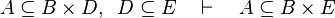
|
||
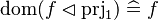
|
||
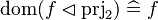
|
||
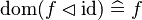
|
||
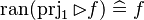
|
||
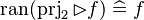
|
||
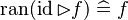
|
||
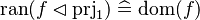
|
||
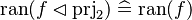
|
||
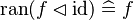
|
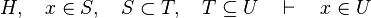
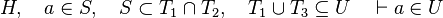
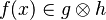
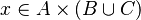
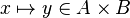
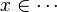
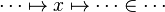
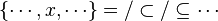
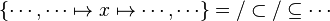
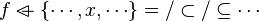
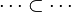
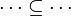

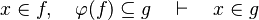

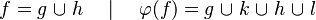
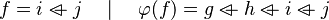
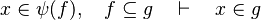

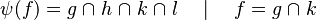
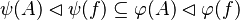
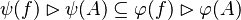
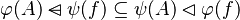
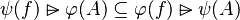
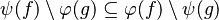
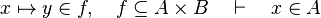
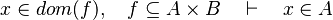
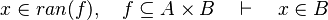
![name\;of\;the\;rule\quad\frac{predicate\;of\;first\;antecedent\cdots predicate\;of\;last\;antecedent}{consequent\;of\;that\;rule}\left[parameters\right]](/images/math/7/3/8/738ee7373b0e1a92b55d65082dd2382e.png)
![Hypothesis\quad\frac{}{predicate}\left[predicate\right]](/images/math/1/7/a/17abab213beec189eb50a58ce52ee038.png)
![IncludeBunion\quad\frac{A\bunion B\bunion C\bunion D\subseteq Z}{B\bunion C\subseteq Z}\left[B,~C\right]](/images/math/4/6/9/469e996832deebc54629c725dcb9920a.png)
![Composition\quad\frac{x\in A,~A\subseteq B}{x\in B}\left[~\right]](/images/math/9/8/3/983d29f85e3242414072ee357ca55f1b.png)