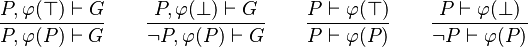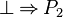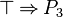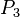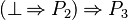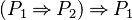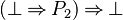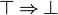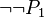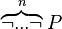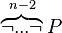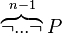Difference between revisions of "Modus Ponens generalized"
imported>Billaude (New page: This page describe the design of a tactic replacing a predicate <math> P </math> in either an hypothesis or a goal by <math>\btrue</math> (respectively <math>\bfalse</math> ) if <math>P</m...) |
imported>Billaude |
||
| Line 1: | Line 1: | ||
| − | This page | + | This page describes the design of a tactic replacing a predicate <math> P </math> in either an hypothesis or a goal by <math>\btrue</math> (respectively <math>\bfalse</math> ) if <math>P</math> (respectively <math>\lnot P</math>) is an hypothesis. That tactic is slightly different from the one requested : [https://sourceforge.net/tracker/?func=detail&aid=3137918&group_id=108850&atid=651672 Feature Request #3137918] |
| Line 16: | Line 16: | ||
= Legacy = | = Legacy = | ||
| − | There already | + | There already exists a reasoner that does a part of that tactic : autoImpF (ImpE automatic). It looks for implicative hypothesis in a sequent. Among the predicates computed by breaking possible conjunctions in the left side of the implication, it checks if some appear in selected hypothesis. In that case, every predicates which are hypothesis (global or local) are removed from the left-sided-predicate of the implication. If it remains no predicates, then the right side of the implication is re-written as a list of conjunction, else implication is re-written without the removed predicates (possibly none). |
Then this reasoner can be considered as "intelligent" because it finds itself the positions where apply, which infer a code hard to read. On the contrary, as reasoners are in the trust-base, they should be easily understandable. | Then this reasoner can be considered as "intelligent" because it finds itself the positions where apply, which infer a code hard to read. On the contrary, as reasoners are in the trust-base, they should be easily understandable. | ||
| Line 74: | Line 74: | ||
= Implementation = | = Implementation = | ||
| − | In this part is explained how the previous choices have been implemented with Java. | + | In this part is explained how the previous choices have been implemented with Java. To do so, a new re-writer has been created : EquivalenceRewriter. For a given predicate, it substitutes every occurrence of a predicate by another one. Those two last are parameters of the re-writer. |
| − | First, every hypothesis | + | # First, every hypothesis of the sequent is stocked in a Set called hypSet. If the hypothesis is a negation (e.g. <math> \lnot P</math>) then its child (<math>P</math>) is actually the predicate stored in the set. |
| + | # | ||
| + | #* Then the goal is analyzed, i.e. each sub-predicate is compared to the predicates contained in hypSet (the set of hypotheses). If there is a match, the predicate is stored in a set (modifGoalSet), else, children of the sub-predicate are analyzed in the same way. Finally, the set contains all the sub-predicate that can be replaced in the goal. But, the goal itself cannot be contained in that set. If it was the case, it would mean that the goal (or its negation) is an hypothesis, and a tactic already process that case. Also, if the goal is a negation, then the first child cannot be contained in the set for the same reasons. | ||
| + | #*Visible (or selected) hypotheses are analyzed like the goal. The only difference is that information are stored in a map (modifHypMap) : the key is the hypothesis to be re-written, the value is a set of all the sub-predicate that can be replaced. As for the goal, the hypothesis (or its child if the hypothesis is a negation) cannot be contained in that set. | ||
| + | # | ||
| + | #*Afterwards, goal is re-written using the equivalenceRewriter. For each predicate in the set modifGoalSet, we check if it is (or its negation) actually an hypothesis of the sequent. If so, we replace it by <math>\btrue</math> (or <math>\bfalse</math>). Then, we catch the re-written goal and the hypotheses needed to achieve it. | ||
| + | #*We proceed the same for hypothesis of the map modifHypMap. At the end, all IHypAction are stored in a List. | ||
| + | #Finally, the proof rule is made. There are 4 cases : | ||
| + | #* the goal is re-written but not the hypotheses : an antecedent is created with no IHypAction, and the IProofRule is made with the needed hypotheses. | ||
| + | #* the goal and hypotheses are re-written : an antecedent is created with the IHypAction computed, and the IProofRule is made with the needed hypotheses. | ||
| + | #* hypotheses are re-written but not the goal : the IProofRule is made with the IHypAction computed. | ||
| + | #* nothing has been re-written : the tactic is no more applicable. | ||
| − | + | Currently, that implementation has few drawbacks. | |
| + | * The most important is that the tactic is not deterministic after one execution. It is due to the EquivalenceRewriter. We don't choose exactly where to apply the substitution. | ||
| + | ** So, for the following predicates : | ||
| + | *** <math>\lnot P_1</math> | ||
| + | *** <math>P_1 \limp P_2</math> | ||
| + | *** <math>(P_1 \limp P_2) \limp P_1</math> | ||
| + | ** it can be re-written either as here-below if we first replace <math>P_1</math> in the third predicate : | ||
| + | *** <math>\lnot P_1</math> | ||
| + | *** <math>\bfalse \limp P_2</math> | ||
| + | *** <math>(\bfalse \limp P_2) \limp \bfalse</math> | ||
| + | ** or like this if we first replace <math>P_1 \limp P_2</math> : | ||
| + | *** <math>\lnot P_1</math> | ||
| + | *** <math>\bfalse \limp P_2</math> | ||
| + | *** <math>\btrue \limp \bfalse</math> | ||
| + | * Moreover, when there are multiple negation (e.g. <math>\lnot\lnot\lnot P</math>), that tactic does not work well: | ||
| + | ** So, for the following predicates, no replacement will be proceeded : | ||
| + | *** <math>\lnot\lnot P_1</math> | ||
| + | *** <math>P_1</math> | ||
| + | ** whereas for those one, replacement can be proceeded on the second one : | ||
| + | *** <math>\lnot\lnot P_1</math> | ||
| + | *** <math>\lnot P_1</math> | ||
| + | ** re-written as following : | ||
| + | *** <math>\lnot\lnot P_1</math> | ||
| + | *** <math>\bfalse</math> | ||
| + | ** Thus, with those two predicates, there is no re-writing possible. | ||
| + | *** <math>\overbrace{\lnot ... \lnot}^{n}P</math> | ||
| + | *** <math>\overbrace{\lnot ... \lnot}^{n-2}P</math> | ||
| + | ** Whereas with these two re-writing is possible. | ||
| + | *** <math>\overbrace{\lnot ... \lnot}^{n}P</math> | ||
| + | *** <math>\overbrace{\lnot ... \lnot}^{n-1}P</math> | ||
| − | + | That's all folks ! | |
Revision as of 13:11, 12 May 2011
This page describes the design of a tactic replacing a predicate 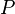 in either an hypothesis or a goal by
in either an hypothesis or a goal by 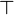 (respectively
(respectively 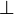 ) if
) if 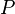 (respectively
(respectively 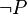 ) is an hypothesis. That tactic is slightly different from the one requested : Feature Request #3137918
) is an hypothesis. That tactic is slightly different from the one requested : Feature Request #3137918
Objective
A sequent can be simplified by finding every occurrence of an hypothesis in the others hypothesis or goal, and replacing it by 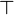 or
or 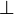 as explained below:
as explained below:
Contrary to the Feature Request, the rule is applied on every occurrence of 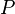 and not only on the one appearing in a disjunctive form. Also, not to make explode the analyzing-time of a sequent, only goal and visible (or selected, it is still in discussion) hypothesis can be re-written, using every hypothesis (global and local). The analyzing-time performance of a sequent can be problematic since every predicate of goal and visible (or selected) hypothesis are checked. But it is still worthy because it may simplify a lot, and so make proof obligation more legible to humans.
and not only on the one appearing in a disjunctive form. Also, not to make explode the analyzing-time of a sequent, only goal and visible (or selected, it is still in discussion) hypothesis can be re-written, using every hypothesis (global and local). The analyzing-time performance of a sequent can be problematic since every predicate of goal and visible (or selected) hypothesis are checked. But it is still worthy because it may simplify a lot, and so make proof obligation more legible to humans.
Legacy
There already exists a reasoner that does a part of that tactic : autoImpF (ImpE automatic). It looks for implicative hypothesis in a sequent. Among the predicates computed by breaking possible conjunctions in the left side of the implication, it checks if some appear in selected hypothesis. In that case, every predicates which are hypothesis (global or local) are removed from the left-sided-predicate of the implication. If it remains no predicates, then the right side of the implication is re-written as a list of conjunction, else implication is re-written without the removed predicates (possibly none).
Then this reasoner can be considered as "intelligent" because it finds itself the positions where apply, which infer a code hard to read. On the contrary, as reasoners are in the trust-base, they should be easily understandable.
Modifications are provided to make it more legible.
Design Decision
The main drawback of this tactic is its execution time. Indeed, each (actually it is not the case but it helps to see how greedy this tactics can be) sub-predicate of each goal and visible (or selected) hypothesis is compared to the others hypothesis (global and local). Several strategies can be applied in order to reduce that execution-time :
- Each hypothesis must be scanned only once to avoid accumulating predicate's running time. From that point of view, two decisions can be inferred :
- A given predicate is compared once to every hypothesis. For instance, we do not try to find every occurrence of an hypothesis among the goal and the visible (or selected) hypothesis. In that case, each predicate would be scanned many times, accumulating execution time.
- That tactic apply the rules specified here-above everywhere it is possible. Thus, from this set of hypothesis :
- We will reach immediatly :
- Which will be re-written to :
- Instead of writing :
- Re-written :
- And then :
- Re-written :
- When a predicate match an hypothesis, its children must not be analyzed.
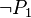
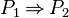

- In that example, the sub-predicate
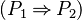 of the third predicate match to the second one. It has to be replaced by
of the third predicate match to the second one. It has to be replaced by 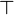 , and all its children have to be not analyzed (even if
, and all its children have to be not analyzed (even if 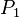 could have been replaced by
could have been replaced by 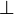 because of the first predicate).
because of the first predicate).
- In the case of n-ary predicates, each possibility is not tested.
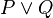
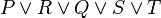
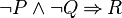
- In that example,
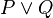 could be replaced by
could be replaced by 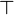 in the second predicate. In order not to add more calculation time, this kind of replacement is not computed.
in the second predicate. In order not to add more calculation time, this kind of replacement is not computed.
That reasoner can be considered as "intelligent", similarly to autoImpF because it computes by its own where it has to apply the rules.
Implementation
In this part is explained how the previous choices have been implemented with Java. To do so, a new re-writer has been created : EquivalenceRewriter. For a given predicate, it substitutes every occurrence of a predicate by another one. Those two last are parameters of the re-writer.
- First, every hypothesis of the sequent is stocked in a Set called hypSet. If the hypothesis is a negation (e.g.
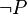 ) then its child (
) then its child (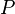 ) is actually the predicate stored in the set.
) is actually the predicate stored in the set. -
- Then the goal is analyzed, i.e. each sub-predicate is compared to the predicates contained in hypSet (the set of hypotheses). If there is a match, the predicate is stored in a set (modifGoalSet), else, children of the sub-predicate are analyzed in the same way. Finally, the set contains all the sub-predicate that can be replaced in the goal. But, the goal itself cannot be contained in that set. If it was the case, it would mean that the goal (or its negation) is an hypothesis, and a tactic already process that case. Also, if the goal is a negation, then the first child cannot be contained in the set for the same reasons.
- Visible (or selected) hypotheses are analyzed like the goal. The only difference is that information are stored in a map (modifHypMap) : the key is the hypothesis to be re-written, the value is a set of all the sub-predicate that can be replaced. As for the goal, the hypothesis (or its child if the hypothesis is a negation) cannot be contained in that set.
-
- Afterwards, goal is re-written using the equivalenceRewriter. For each predicate in the set modifGoalSet, we check if it is (or its negation) actually an hypothesis of the sequent. If so, we replace it by
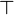 (or
(or 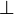 ). Then, we catch the re-written goal and the hypotheses needed to achieve it.
). Then, we catch the re-written goal and the hypotheses needed to achieve it. - We proceed the same for hypothesis of the map modifHypMap. At the end, all IHypAction are stored in a List.
- Afterwards, goal is re-written using the equivalenceRewriter. For each predicate in the set modifGoalSet, we check if it is (or its negation) actually an hypothesis of the sequent. If so, we replace it by
- Finally, the proof rule is made. There are 4 cases :
- the goal is re-written but not the hypotheses : an antecedent is created with no IHypAction, and the IProofRule is made with the needed hypotheses.
- the goal and hypotheses are re-written : an antecedent is created with the IHypAction computed, and the IProofRule is made with the needed hypotheses.
- hypotheses are re-written but not the goal : the IProofRule is made with the IHypAction computed.
- nothing has been re-written : the tactic is no more applicable.
Currently, that implementation has few drawbacks.
- The most important is that the tactic is not deterministic after one execution. It is due to the EquivalenceRewriter. We don't choose exactly where to apply the substitution.
- So, for the following predicates :
- it can be re-written either as here-below if we first replace
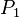 in the third predicate :
in the third predicate :
- or like this if we first replace
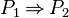 :
:
- So, for the following predicates :
- Moreover, when there are multiple negation (e.g.
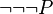 ), that tactic does not work well:
), that tactic does not work well:
- So, for the following predicates, no replacement will be proceeded :
- whereas for those one, replacement can be proceeded on the second one :
- re-written as following :
- Thus, with those two predicates, there is no re-writing possible.
- Whereas with these two re-writing is possible.
- So, for the following predicates, no replacement will be proceeded :
That's all folks !