Rodin Proof Tactics: Difference between revisions
imported>Benoit |
imported>Benoit |
||
| Line 620: | Line 620: | ||
== Bounded Goal with Finite Hypothesis == | == Bounded Goal with Finite Hypothesis == | ||
* '''Description''': Discharges a sequent whose goal states that an expression E has a lower or a upper bound (e.g. | * '''Description''': Discharges a sequent whose goal states that an expression E has a lower or a upper bound (e.g. ∃n·(∀x·x ∈ S ⇒ x ≤ n)), when there is an hypothesis that states the finiteness of E (i.e. finite(S)). | ||
* '''Additional details''': | * '''Additional details''': | ||
{{InfRule|FIN_L_LOWER_BOUND_L|<math>\frac{}{\textbf{H},\;\finite(S) \;\;\vdash \;\; \exists n\,\qdot\, (\forall x \,\qdot\, x \in S \;\limp\; n \leq x)}</math>}} | |||
{{InfRule|FIN_L_LOWER_BOUND_R|<math>\frac{}{\textbf{H},\;\finite(S) \;\;\vdash \;\; \exists n\,\qdot\, (\forall x \,\qdot\, x \in S \;\limp\; x \geq n)}</math>}} | |||
{{InfRule|FIN_L_UPPER_BOUND_L|<math>\frac{}{\textbf{H},\;\finite(S) \;\;\vdash \;\; \exists n\,\qdot\, (\forall x \,\qdot\, x \in S \;\limp\; n \geq x)}</math>}} | |||
{{InfRule|FIN_L_UPPER_BOUND_R|<math>\frac{}{\textbf{H},\;\finite(S) \;\;\vdash \;\; \exists n\,\qdot\, (\forall x \,\qdot\, x \in S \;\limp\; x \leq n)}</math>}} | |||
* '''ID''': org.eventb.core.seqprover.finiteHypBoundedGoalTac | * '''ID''': org.eventb.core.seqprover.finiteHypBoundedGoalTac | ||
* '''Auto-tactic''': | * '''Auto-tactic''': ''Default'' | ||
* '''Post-tactic''': ''Default'' | |||
* '''Preference Display''': Bounded Goal with finite Hypothesis (Discharge) | |||
* ''' | * '''Interactive''': ''No'' | ||
* ''' | * '''Proving Interface Display''': Existence of minimum or maximum in goal with finite hypothesis | ||
Before [[Image: FiniteHypBoundedGoalBefore.png]] | |||
After [[Image: FiniteHypBoundedGoalAfter.png]] | |||
== Falsify Goal == | == Falsify Goal == | ||
Revision as of 16:34, 21 January 2011
This page contains descriptions of the available proof tactics within the RODIN Platform.
For each tactic, the descriptions is as follows:
- Description: A high-level description of the tactic. This will be the description appeared in the RODIN Platform preferences.
- Additional details: Details explanation of the tactic, when it is applicable, give the associated proof rule. See Inference rules list and Rewriting rules list.
- ID: An unique ID associated with the tactic.
- Auto-tactic: No: the tactic cannot be added as an auto-tactic. Yes: the tactic can be added as an auto-tactic. Default: the tactic is a default auto-tactic.
- Post-tactic: No: the tactic cannot be added as a post-tactic. Yes: the tactic can be added as a post-tactic. Default: the tactic is a default post-tactic.
- Preference display: (Optional) If the tactic can be used as an auto-tactic or a post-tactic, information on how the tactic is displayed in the auto-tactic preference or the post-tactic preference.
- Interactive: No: the tactic cannot be invoked interactively from the proving interface. Global: The tactic can be invoked interactively from the Proof Control View. Goal: The tactic can be invoked from the Goal view. Hypothesis: The tactic can be invoked from the Hypothesis view. If the tactic can be invoked interactively (i.e. either Global, Goal or Hypothesis), more information about how this could be done will be given. Note that since the Post-tactics can be launched manually, any tactics that can be included in the post-tactic in principle can be invoked interactively via the post-tactic. Here No only means that there is no separate invocation for this specific tactic.
- Proving interface display: Example(s) on how applications of this tactic can be seen from the proving interface of the RODIN Platform.
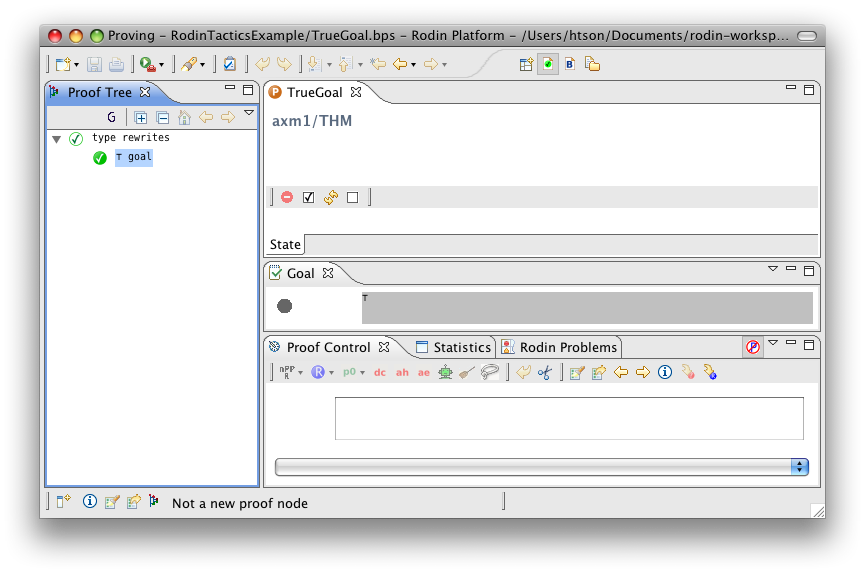
True Goal
- Description: Discharges any sequent whose goal is '⊤' (logical true).
- Additional details:
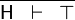
|
TRUE_GOAL |
- ID: org.eventb.core.seqprover.trueGoalTac
- Auto-tactic: Default
- Post-tactic: Default
- Preference display: True Goal (Discharge)
- Interactive: No
- Proving interface display: ⊤ goal
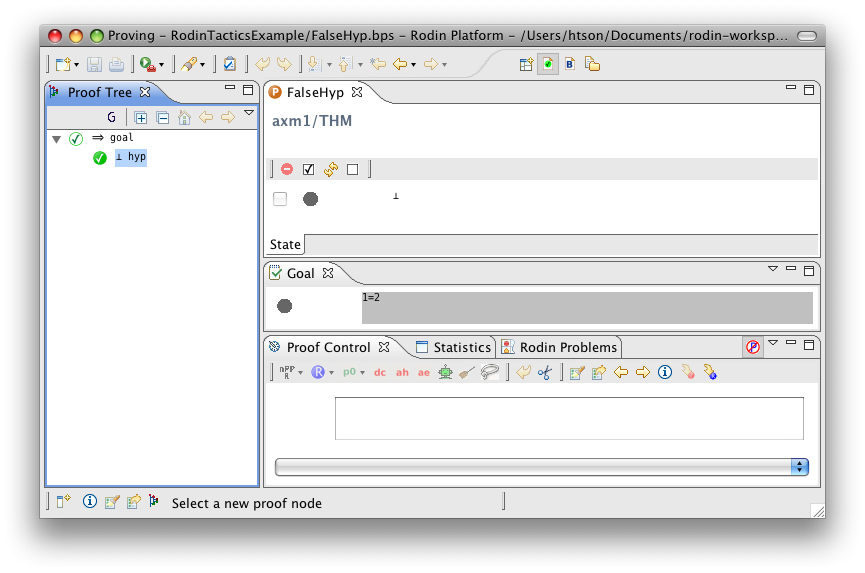
False Hypothesis
- Description: Discharges any sequent containing a '⊥' hypothesis
- Additional details:

|
FALSE_HYP |
- ID: org.eventb.core.seqprover.falseHypTac
- Auto-tactic: Default
- Post-tactic: Default
- Preference display: False Hypothesis (Discharge)
- Interactive: No
- Proving interface display: ⊥ hyp
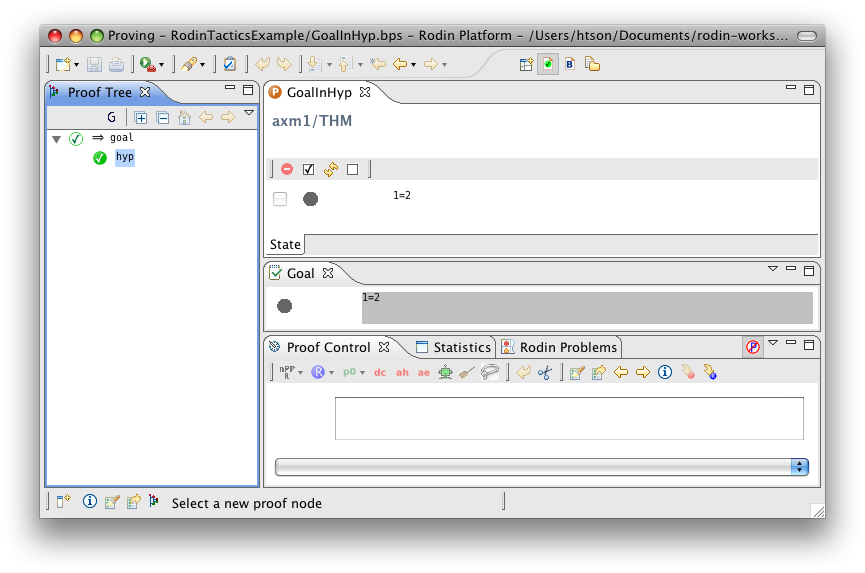
Goal in Hypotheses
- Description: Discharges any sequent whose goal is contained in its hypotheses
- Additional details:
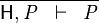
|
HYP |
- ID: org.eventb.core.seqprover.goalInHypTac
- Auto-tactic: Default
- Post-tactic: Default
- Preference display: Goal in Hypotheses (Discharge)
- Interactive: No
- Proving interface display: hyp
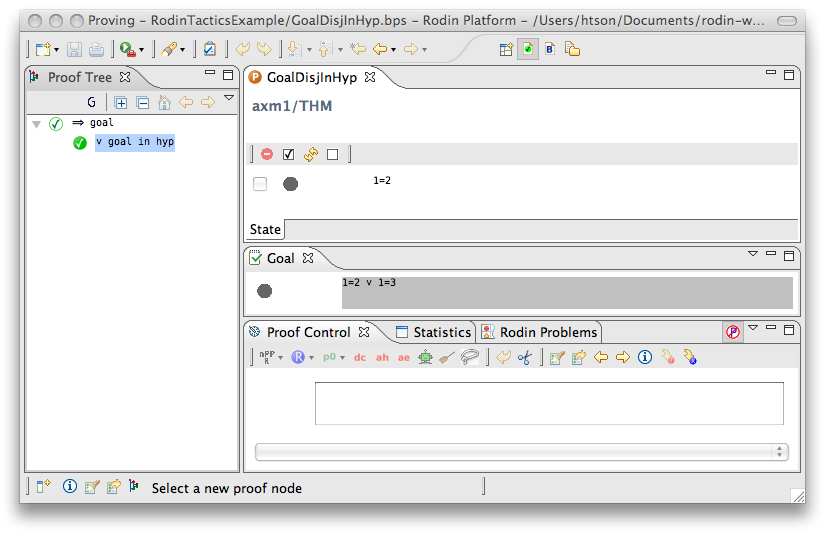
Goal Disjunct in Hypothesis
- Description: Discharges any sequent whose goal is a disjunction and one of whose disjuncts is present in the hypotheses.
- Additional details:
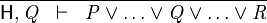
|
HYP_OR |
- ID: org.eventb.core.seqprover.goalDisjInHypTac
- Auto-tactic: No
- Post-tactic: Default
- Preference display: Goal Disjunct in Hypotheses (Discharge)
- Interactive: No
- Proving interface display: ∨ goal in hyp
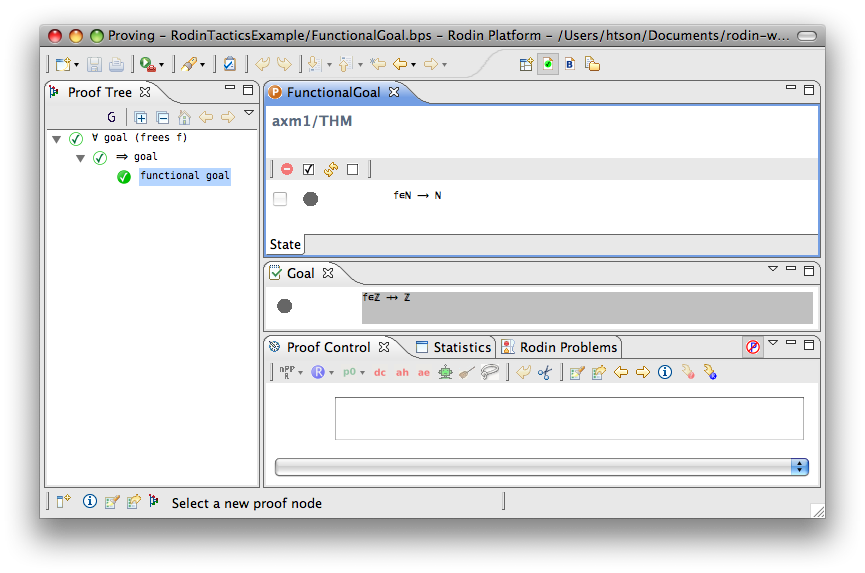
Functional Goal
- Description: Tries to discharge a sequent whose goal states that an expression is a function (i.e. f ∈ T1 ⇸ T2, where T1 and T2 are type expressions).
- Additional details: The sequent is discharged if there is a hypothesis specifying that f is a function of any kind (i.e. partial function, total function, partial injection, total injection, partial surjection, total surjection, bijection). More information about type expressions in Event-B is in the FAQ page. The corresponding proof rule is as follows.
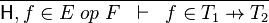
|
FUN_GOAL |
where 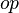 is either
is either  .
.
- ID: org.eventb.core.seqprover.funGoalTac
- Auto-tactic: Default
- Post-tactic: Default
- Preference display: Functional Goal (Discharge)
- Interactive: No
- Proving interface display: functional goal
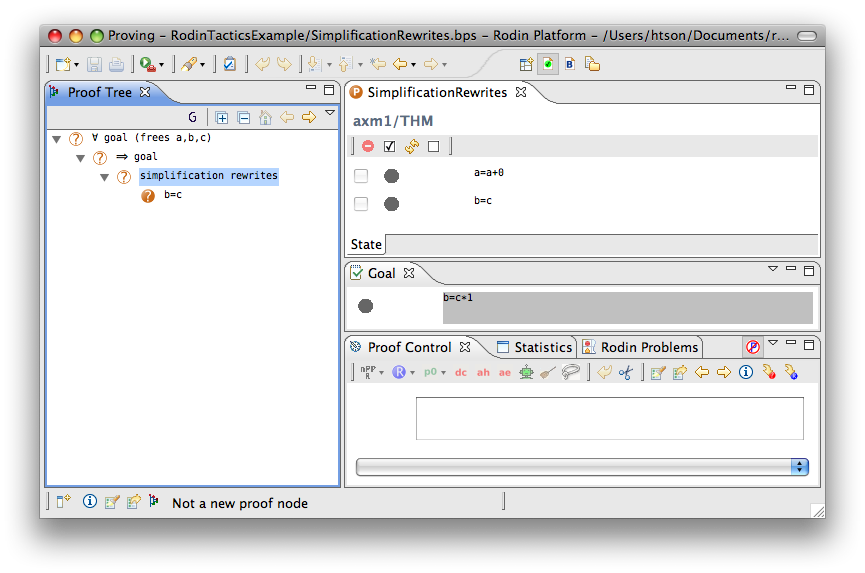
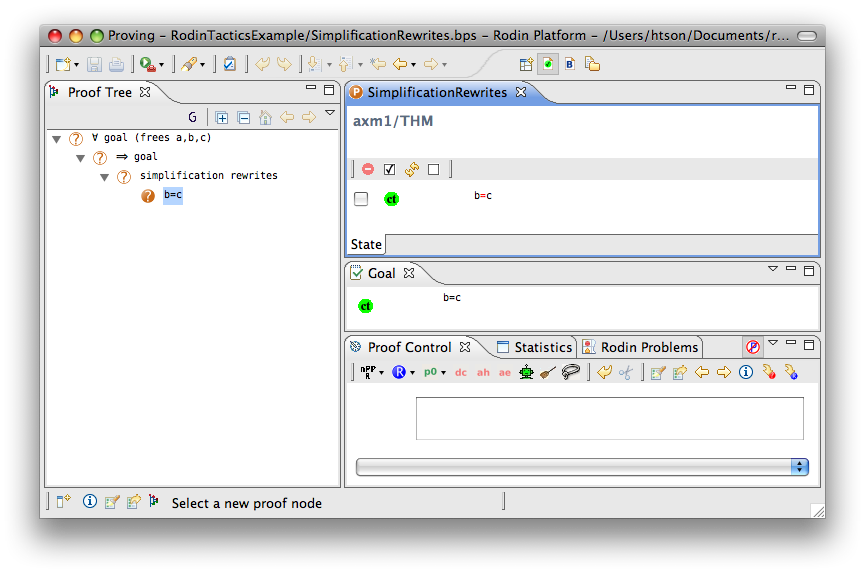
Simplification Rewriter
- Description: Tries to simplify all predicates in a sequent using pre-defined simplification rewriting rules.
- Additional details: The list of rewriting rules are in the following page rewriting rules, which are marked as Automatic.
The corresponding proof rule is as follows.
|
SIM |
where 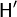 are the set of new hypotheses obtained by rewriting some of the original hypothesis in
are the set of new hypotheses obtained by rewriting some of the original hypothesis in 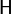 , and
, and 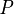 is the rewriting of the original goal
is the rewriting of the original goal 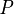 .
.
- ID: org.eventb.core.seqprover.autoRewriteTac
- Auto-tactic: Default
- Post-tactic: Default
- Preference display: Simplification Rewriter (Simplify)
- Interactive: No
- Proving interface display: simplification rewrites
The example below shows the screen-shots of the step before the application of the tactic and the step just after the application of the tactic. There are 3 rewritings have been done as follows.
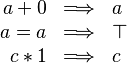
Note that 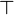 hypothesis is always dropped in the RODIN Platform.
hypothesis is always dropped in the RODIN Platform.
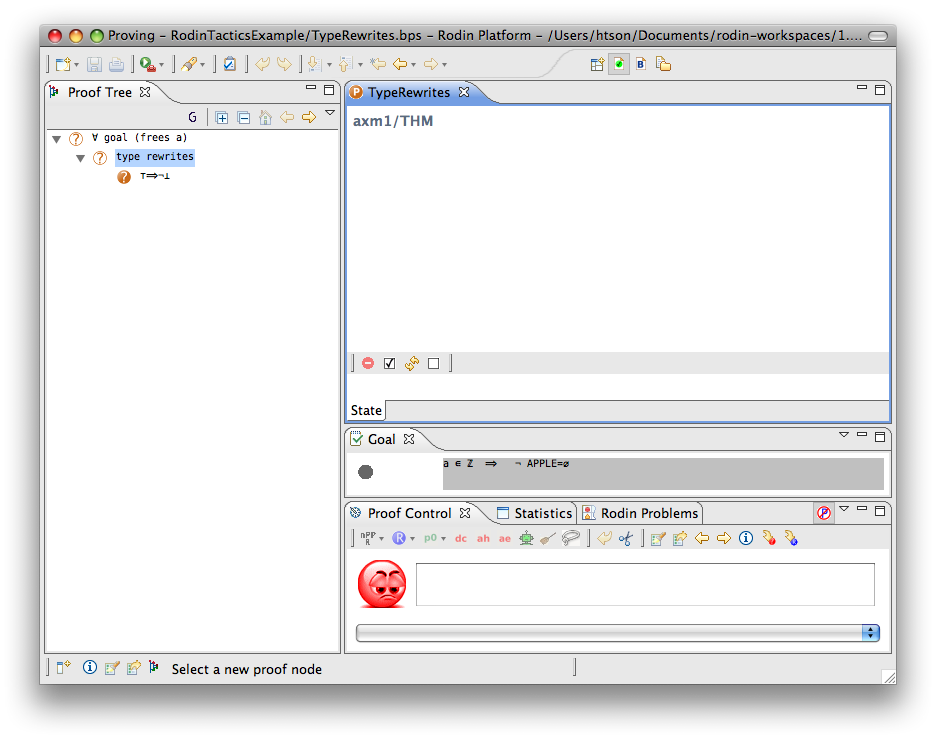
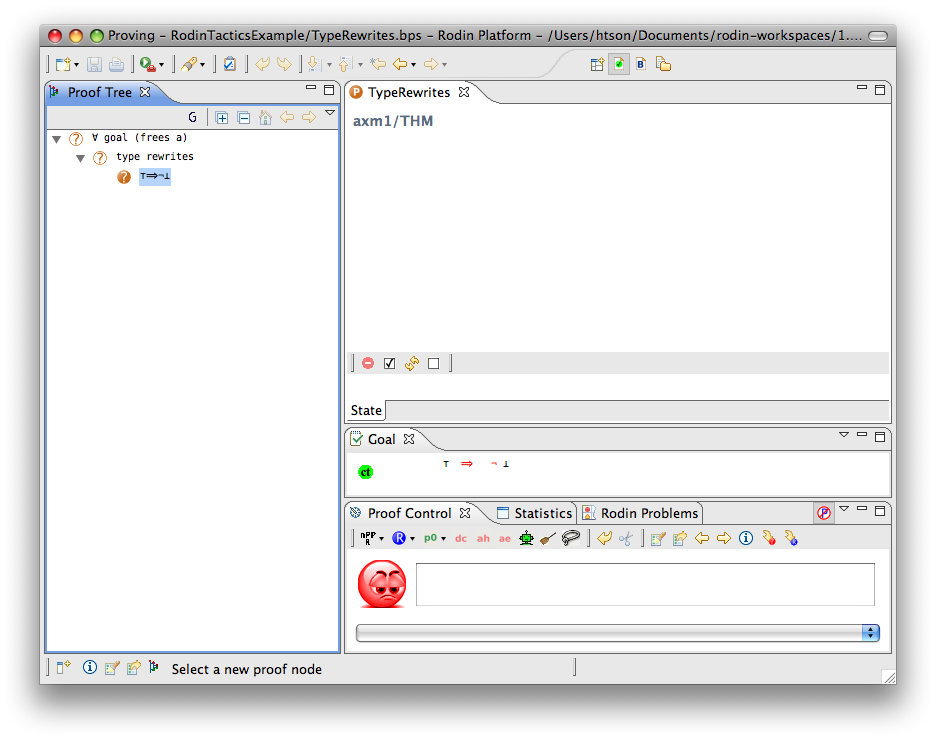
Type Rewriter
- Description: Simplifies predicates containing type expressions such as E ∈ T to ⊤ and T = ∅ to ⊥.
- Additional details: More information about type expressions in Event-B is in the FAQ page.
The rewriting rules are SIMP_TYPE_EQUAL_EMPTY and SIMP_TYPE_IN in the rewriting rules page.
The corresponding proof rule is as follows.
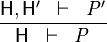
|
SIM |
where  are the set of new hypotheses obtained by rewriting some of the original hypothesis in
are the set of new hypotheses obtained by rewriting some of the original hypothesis in  , and
, and 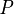 is the rewriting of the original goal
is the rewriting of the original goal 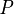 .
.
- ID: org.eventb.core.seqprover.typeRewriteTac
- Auto-tactic: Default
- Post-tactic: Default
- Preference display: Type Rewriter (Simplify)
- Interactive: No
- Proving interface display: type rewrites
The example below shows the screen-shots of the step before the application of the tactic and the step just after the application of the tactic.
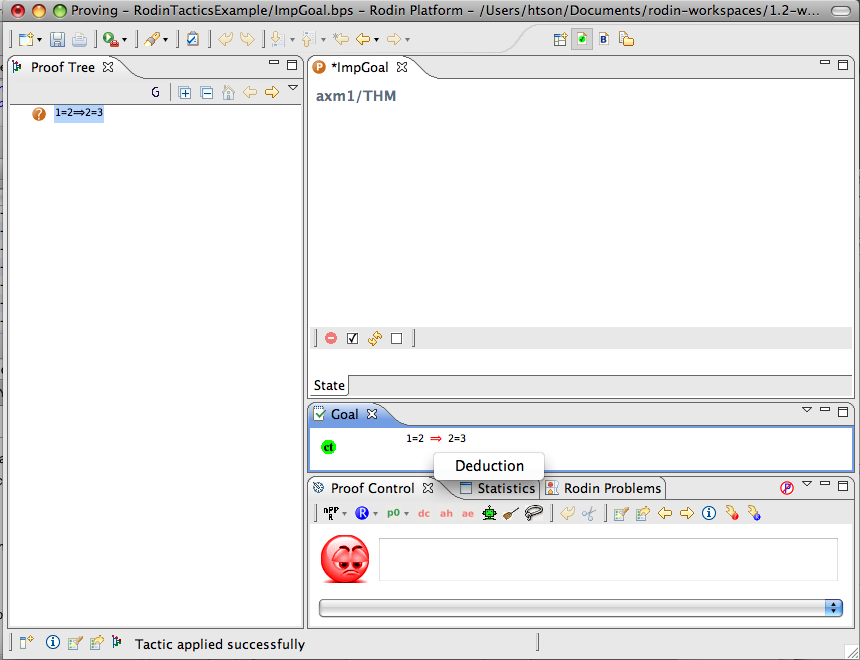
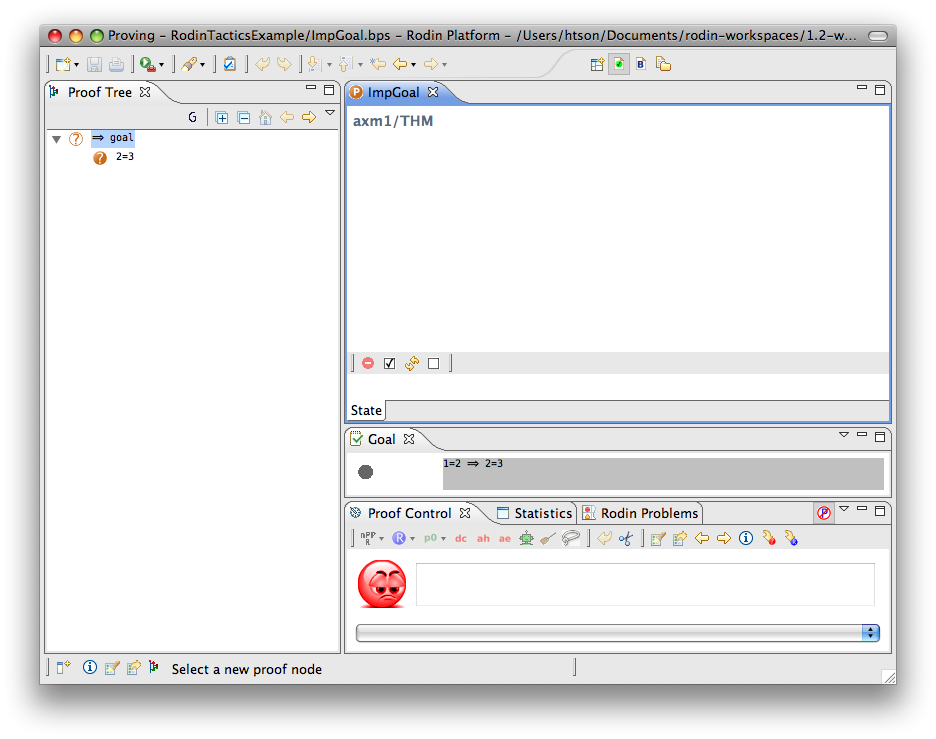
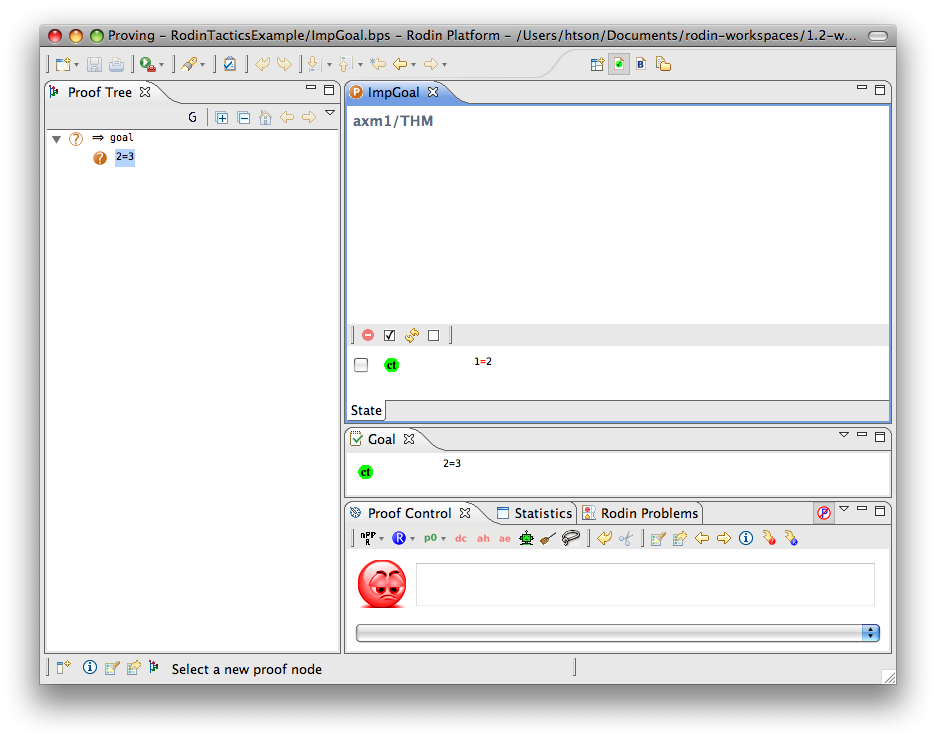
Implication Goal
- Description: Simplifies any sequent with an implicative goal by adding the left hand side of the implication to the hypotheses and making its right hand side the new goal.
- Additional details:
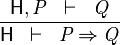
|
IMP_R |
- ID: org.eventb.core.seqprover.impGoalTac
- Auto-tactic: No
- Post-tactic: Default
- Preference display: Implicative Goal (Simplify)
- Interactive: Goal. The
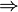 symbol in the implicative goal is redden. When the mouse hovers the red symbol, the label of the tactic in the context menu is Deduction.
symbol in the implicative goal is redden. When the mouse hovers the red symbol, the label of the tactic in the context menu is Deduction.
- Proving interface display: ⇒ goal
The example below shows the screen-shots of the step before the application of the tactic and the step just after the application of the tactic.
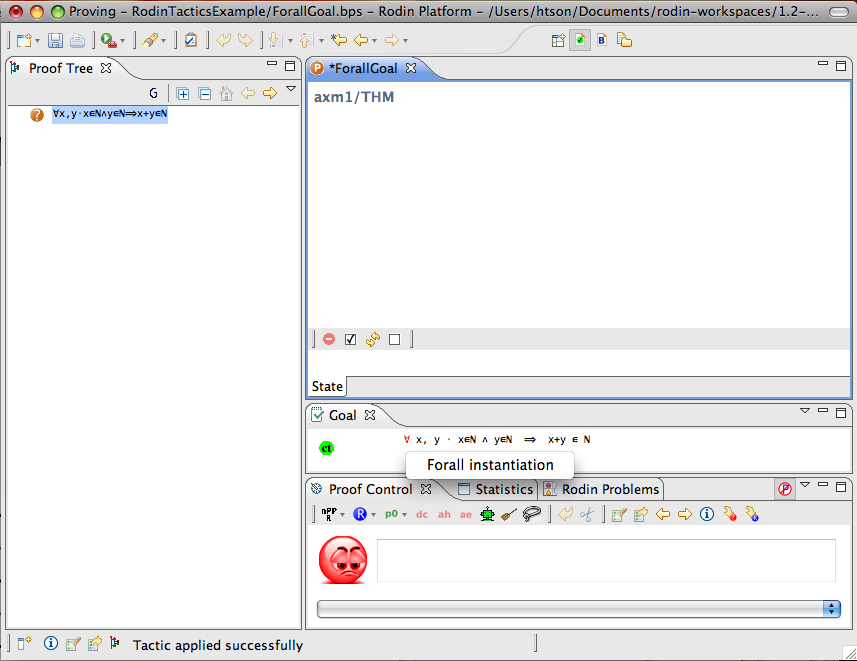
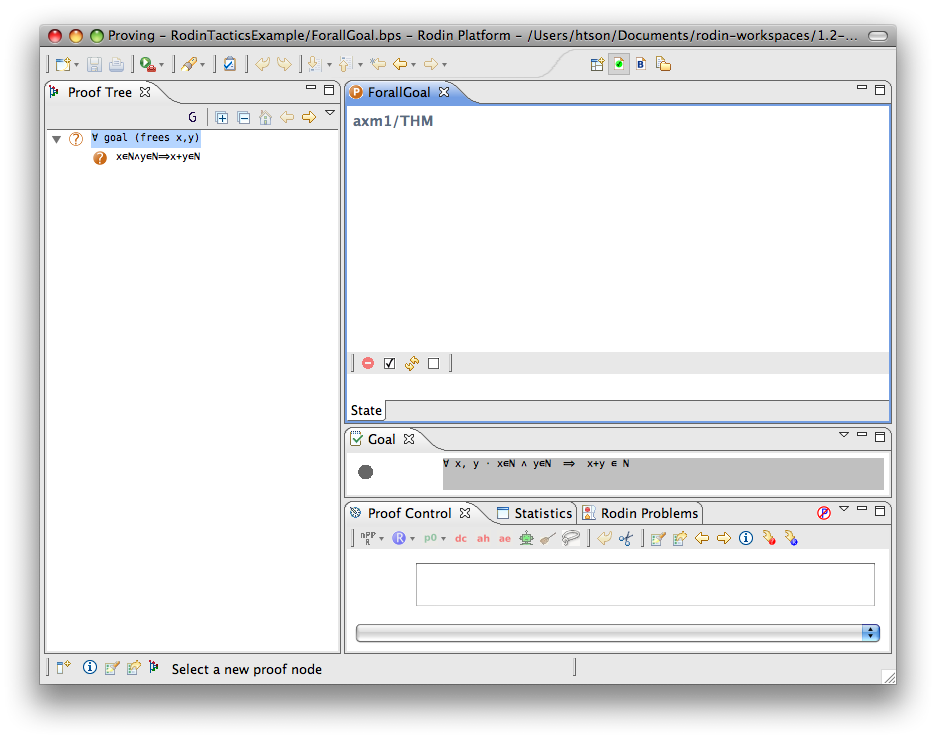
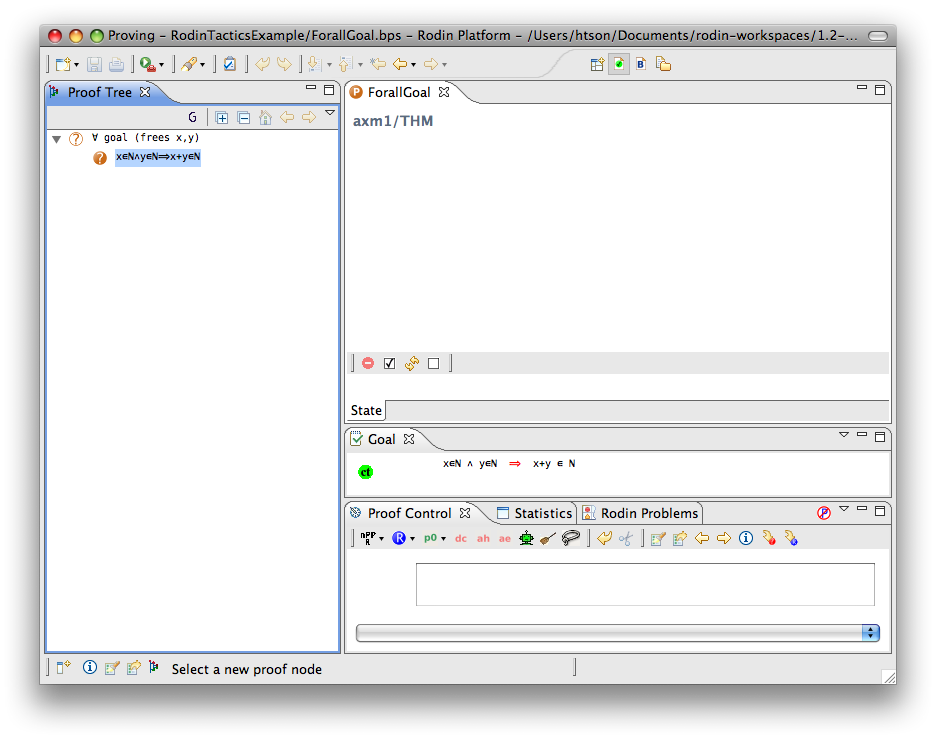
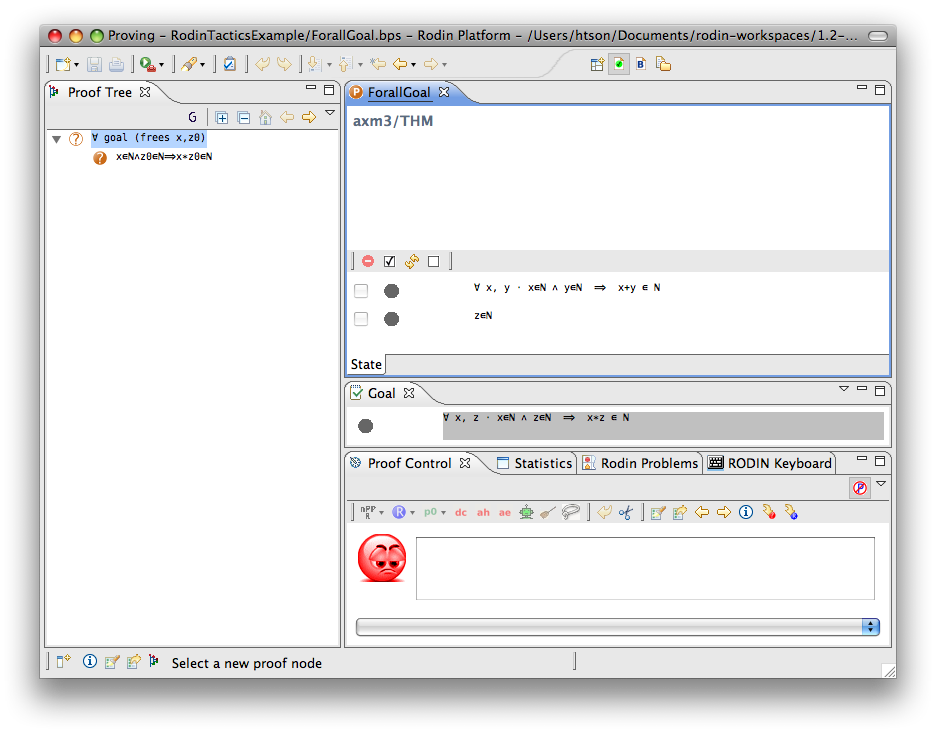
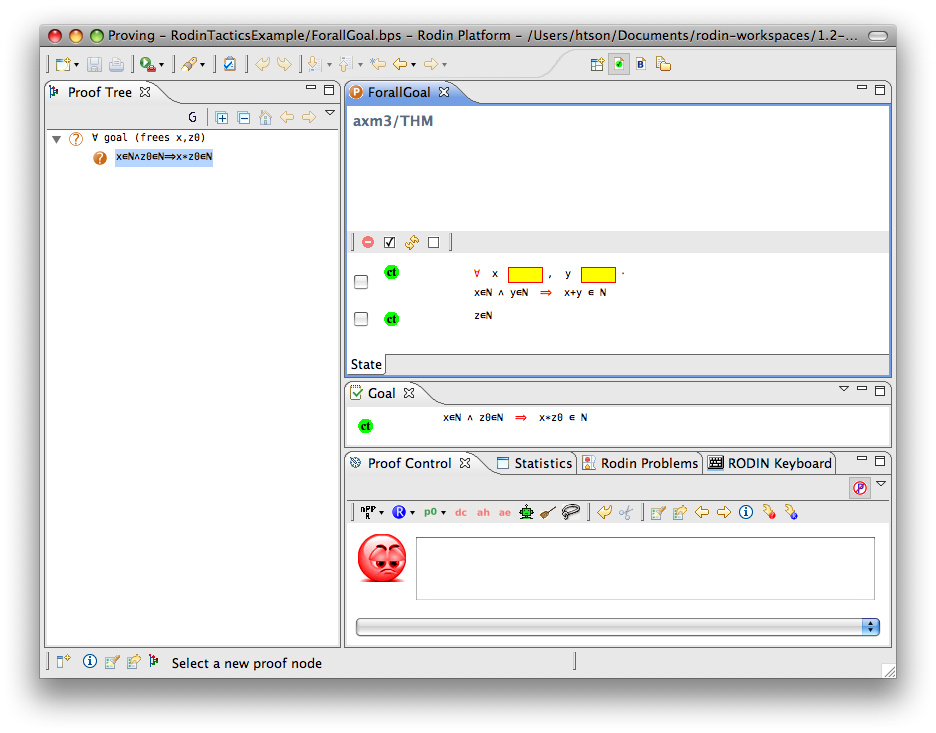
For-all Goal
- Description: Simplifies any sequent with a universally quantified goal by freeing all its bound variables.
- Additional details: The bound variables will be renaming accordingly to avoid name collision.
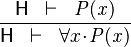
|
ALL_R |
where  does not appear freely in
does not appear freely in 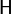 .
.
- ID: org.eventb.core.seqprover.forallGoalTac
- Auto-tactic: No
- Post-tactic: Yes
- Preference display: For-all Goal (Simplify)
- Interactive: Goal. The symbol
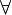 in the universal quantified goal is redden. When the mouse hovers the red symbol, the label of the tactic in the context menu is Forall instantiation.
in the universal quantified goal is redden. When the mouse hovers the red symbol, the label of the tactic in the context menu is Forall instantiation.
- Proving interface display: ∀ goal (frees list-of-bounded-identifiers)
The first example below shows the screen-shots of the step before the application of the tactic and the step just after the application of the tactic. There is no renaming of the bound variable.
The second example below shows the screen-shots of the step before the application of the tactic and the step just after the application of the tactic. The bound variable  is not renamed, but the bound variable
is not renamed, but the bound variable 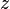 is renamed to
is renamed to 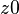 to avoid capture of the existing variable
to avoid capture of the existing variable 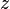 .
.
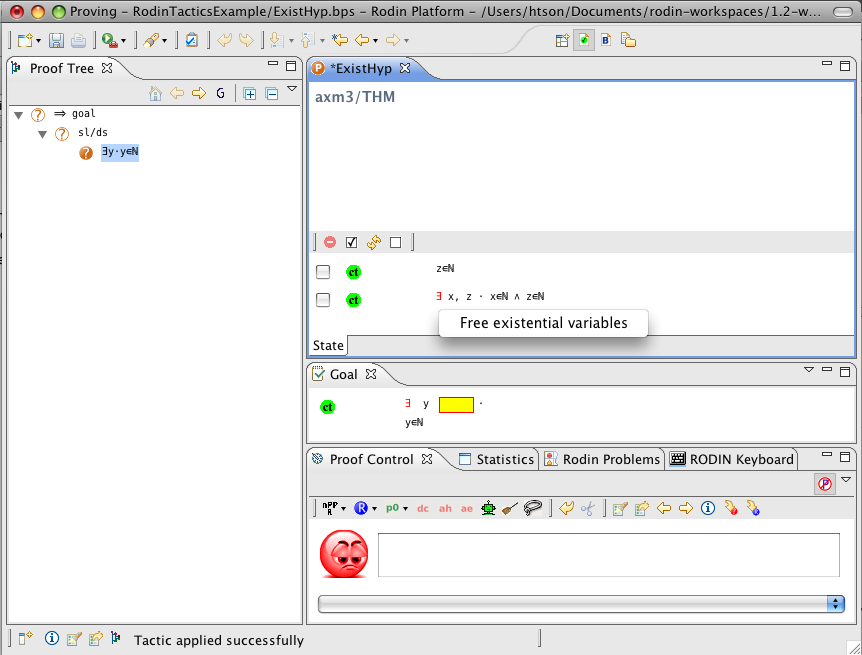
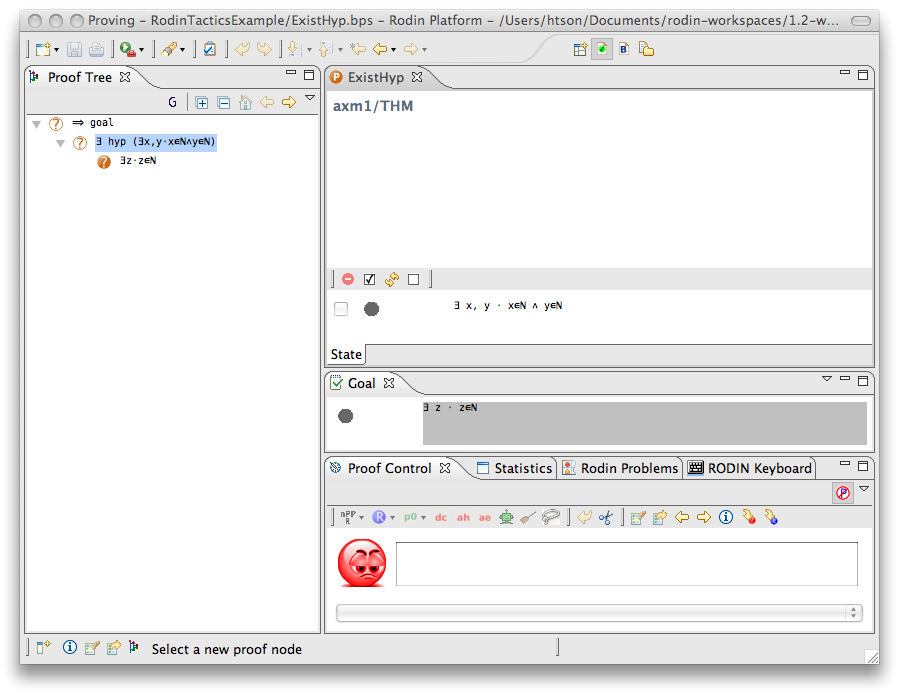
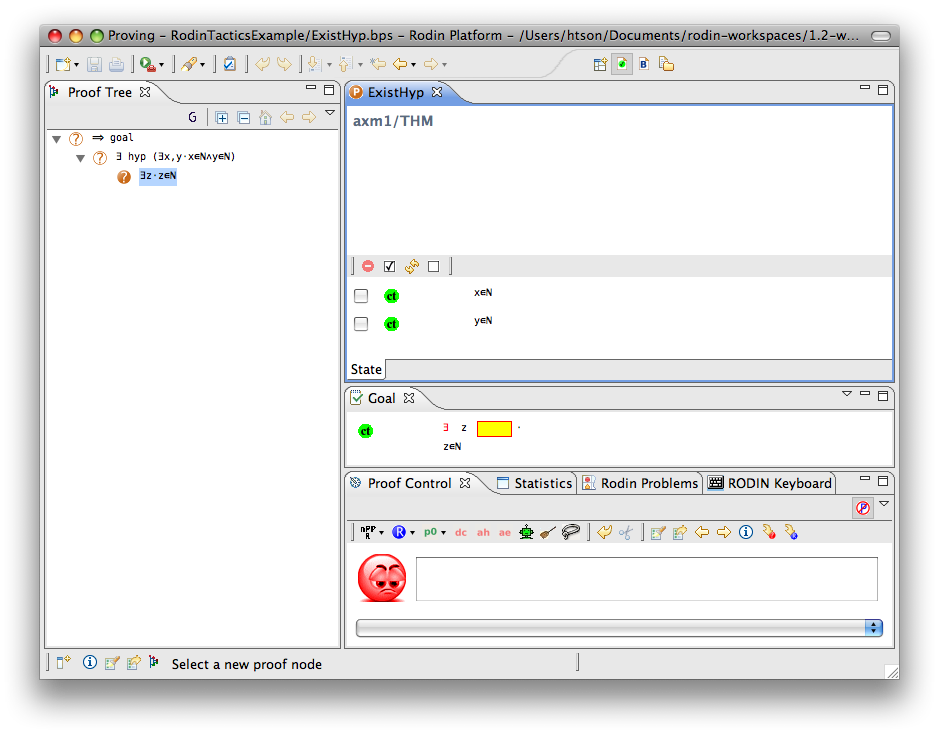
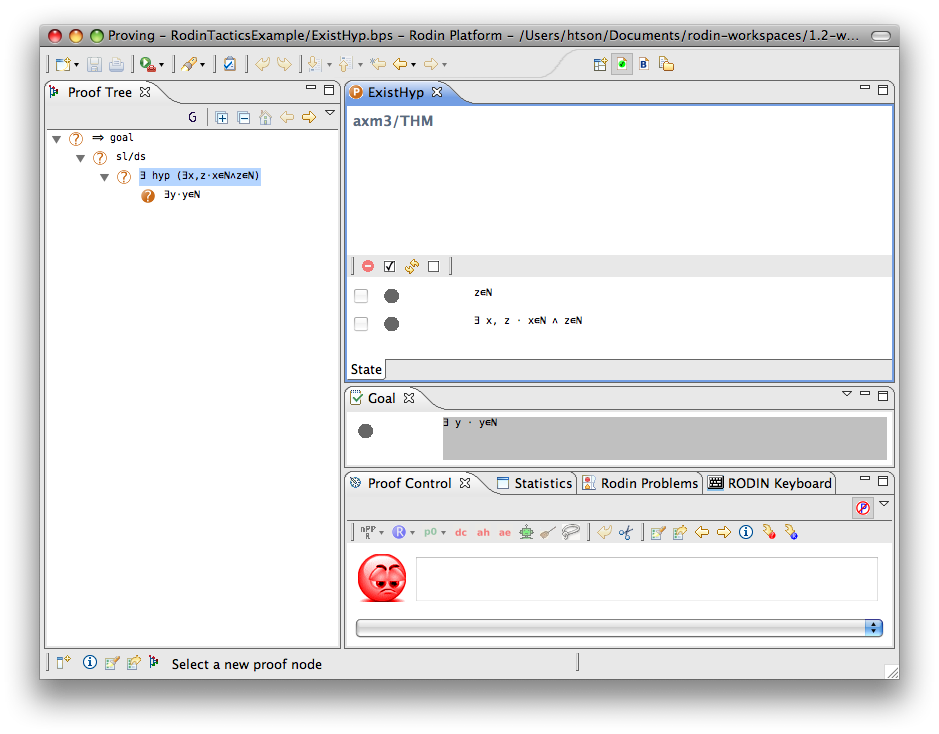
Exists Hypothesis
- Description: In automatic mode (as an auto-tactic or post-tactic), this tactic simplifies any sequent containing existentially quantified hypotheses by freeing their bound variables. In interactive mode, only the selected hypothesis is simplified by freeing its bound variables.
- Additional details: The bound variables will be renaming if necessary to avoid name collision. After freeing their bound variables, if the resulting predicate is a conjunction then it is split into several hypotheses.
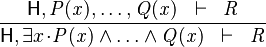
|
XST_L |
where  does not appear freely in
does not appear freely in 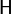 and
and 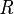 .
.
- ID: org.eventb.core.seqprover.existHypTac
- Auto-tactic: No
- Post-tactic: Default
- Preference display: Exists Hypotheses (Simplify)
- Interactive: Hypothesis. The symbol
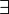 in the existential quantified hypothesis is redden. When the mouse hovers the red symbol, the label of the tactic in the context menu is Free existential variables.
in the existential quantified hypothesis is redden. When the mouse hovers the red symbol, the label of the tactic in the context menu is Free existential variables.
- Proving interface display:
The first example below shows the screen-shots of the step before the application of the tactic and the step just after the application of the tactic. There is no renaming of the bound variable.
The second example below shows the screen-shots of the step before the application of the tactic and the step just after the application of the tactic. The bound variable x is not renamed, but the bound variable z is renamed to z0 to avoid capture of the existing variable z.
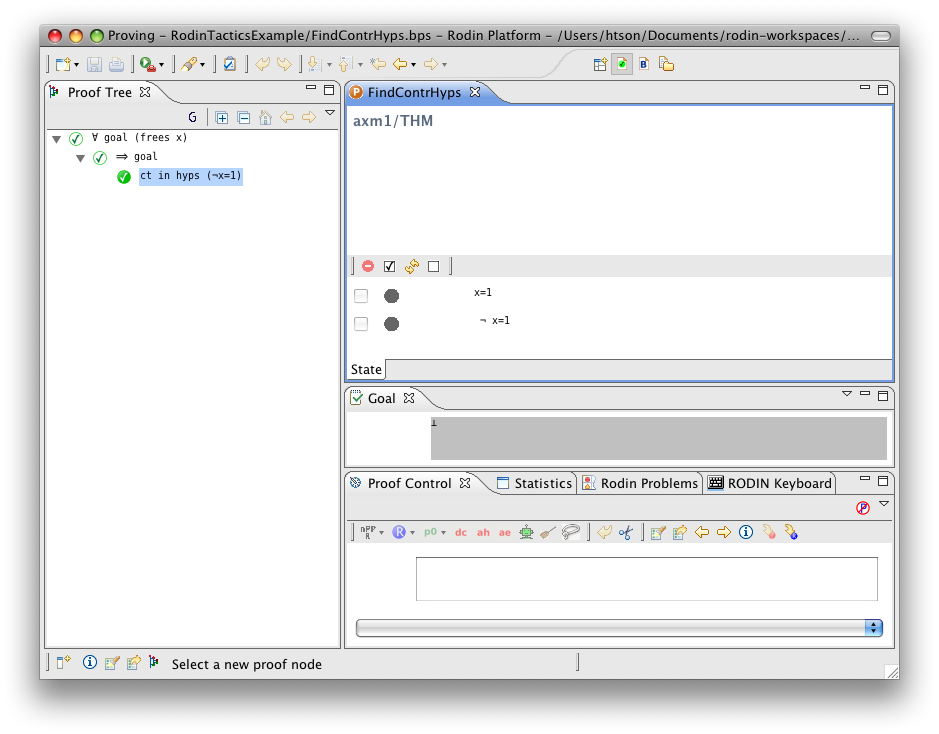
Find Contradictory Hypothesis
- Description: Discharges a sequent by finding contradictory hypotheses, i.e.
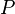 and
and 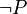 .
.
- Additional details: This tactic tries to find a contradiction using each selected hypothesis that is a negation.
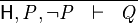
|
CNTR |
- ID: org.eventb.core.seqprover.findContrHypsTac
- Auto-tactic: Default
- Post-tactic: Default
- Preference display: Find Contradictory Hypotheses (Discharge)
- Interactive: No
- Proving interface display: ct in hyps (the negated hypothesis)
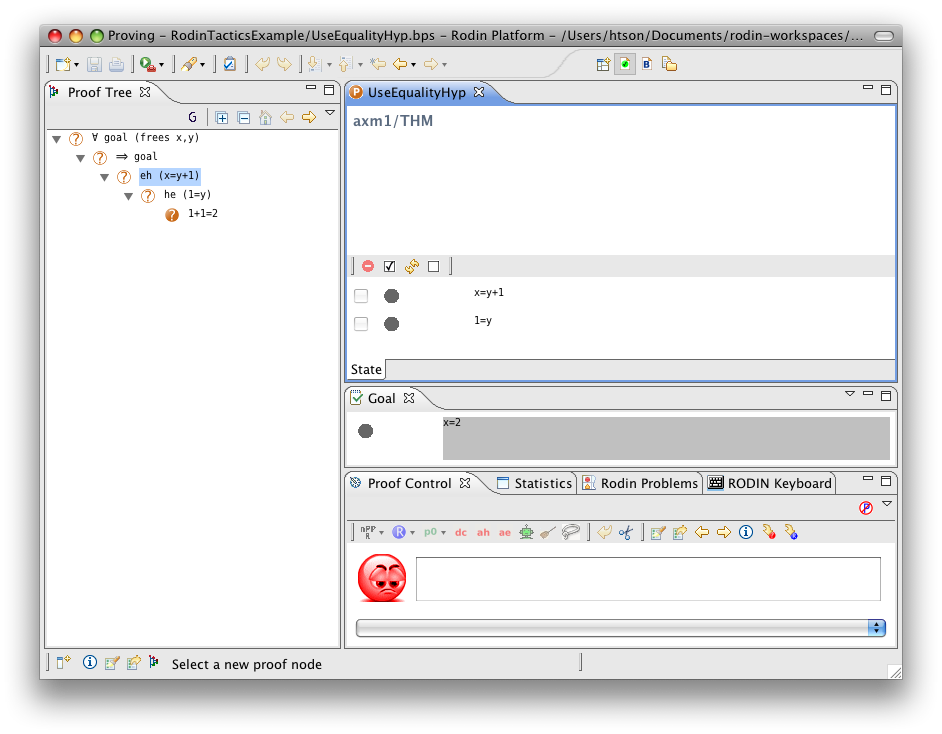
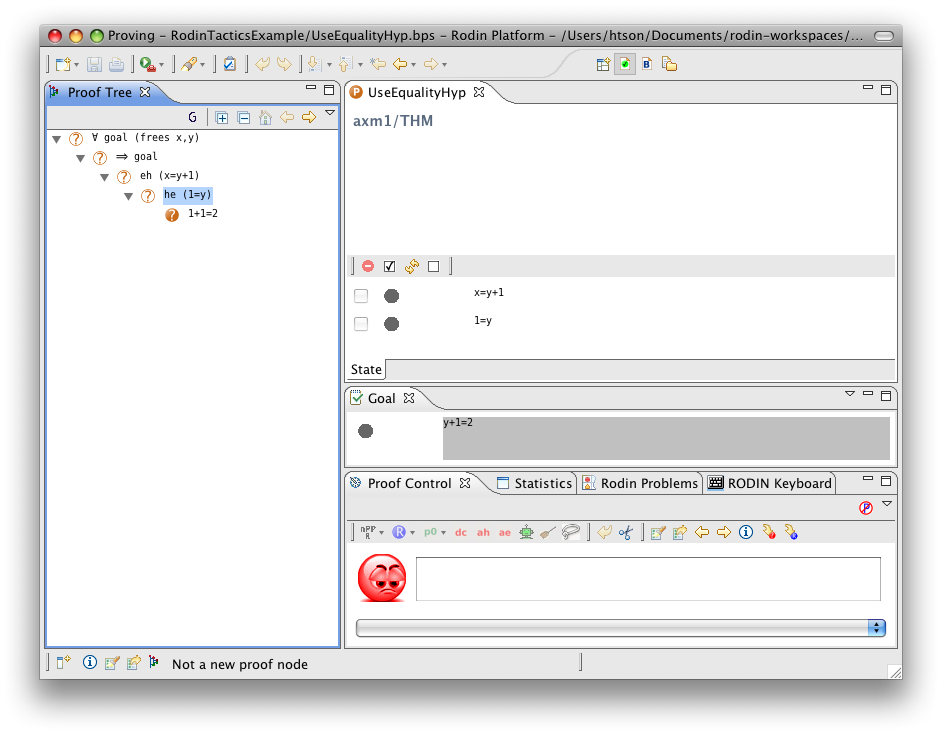
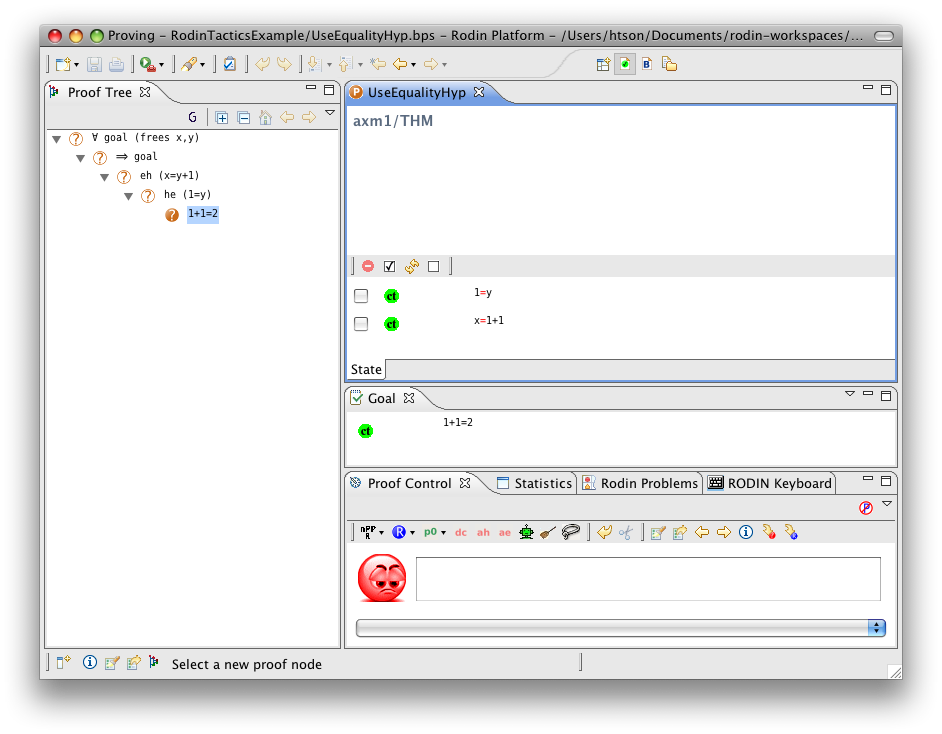
Use Equality Hypothesis
- Description: Simplifies a sequent by rewriting all selected hypotheses and the goal using a (selected) hypothesis that is an equality between a free variable and an expression that does not contain the free variable. The used equality remains in the selected hypotheses to be used again.
- Additional details: Each application of the tactic take only one equality hypothesis into account. If there are several equality hypotheses, they require several applications of the tactic. Moreover, in the case where there are several equality hypotheses, the choice of which hypothesis will be chosen is non-deterministic. This tactic behaves as #Use Equality Hypothesis from Left to Right or #Use Equality Hypothesis from Right to Left depending on if the free variable is on the left or on the right of the equality.
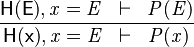
|
EQL_LR |
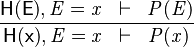
|
EQL_RL |
- ID: org.eventb.core.seqprover.eqHypTac
- Auto-tactic: Default
- Post-tactic: Default
- 'Preference display: Use Equals Hypotheses (Simplify)
- Interactive: Hypothesis. See #Use Equality Hypothesis from Left to Right and #Use Equality Hypothesis from Right to Left
- Proving interface display: eh (the equal hypothesis) in the case where the free variable is on the left-hand side or he (the equal hypothesis) in the case where the free variable is on the right-hand side.
The example below shows the screen-shots of the step before the application of the tactic, the step after the first application of the tactic with hypothesis  and the step just after the second application of the tactic with hypothesis
and the step just after the second application of the tactic with hypothesis 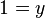 .
.
Use Equality Hypothesis from Left to Right
- Description: Rewriting all selected hypotheses and the goal using a (selected) hypothesis that is an equality between two expressions. The used equality remains in the selected hypotheses to be used again.
- ID:
- Auto-tactic: See #Use Equality Hypothesis
- Post-tactic: See #Use Equality Hypothesis
- Interactive: Hypothesis
- Proving interface display:
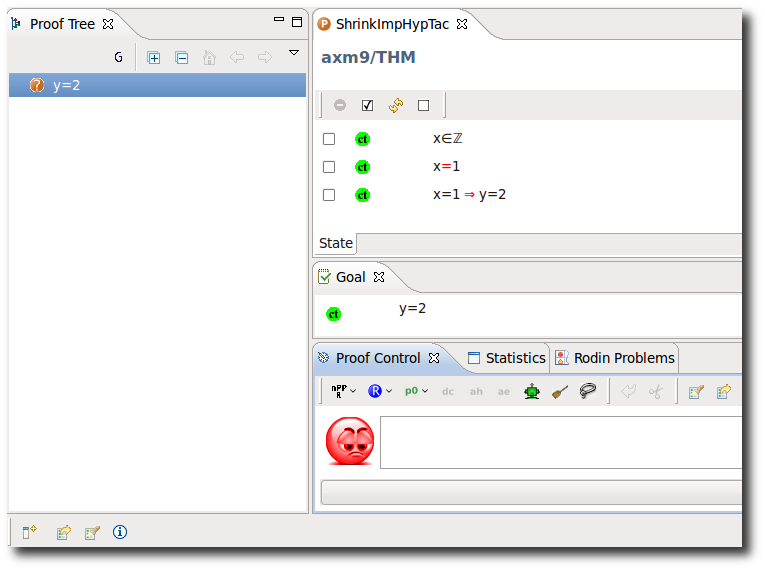
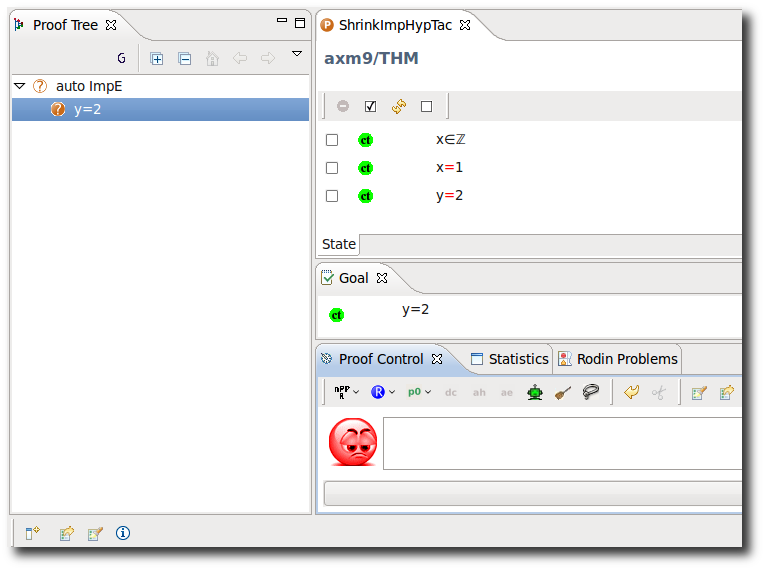
Shrink Implicative Hypothesis
- Description: Simplifies the (visible) implicative hypotheses in a sequent by removing predicates from their left hand sides that are (selected) hypotheses.
- Additional details:
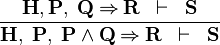
|
AUTO_MH |
- ID: org.eventb.core.seqprover.shrinkImpHypTac
- Auto-tactic: Default
- Post-tactic: Default
- Preference Display: Shrink Implicative Hypotheses (Simplify)
- Interactive: No
- Proving interface display: auto ImpE
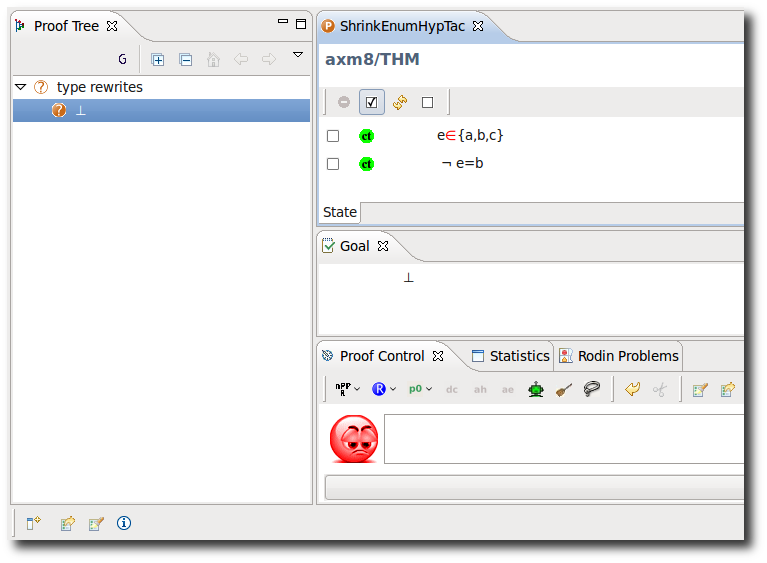
Shrink Enumerated Set
- Description: Simplifies (selected) hypotheses of the form e ∈ {a,b,c} to e ∈ {a,c} after finding the hypothesis ¬ e = b.
- Additional details: TODO
- ID: org.eventb.core.seqprover.shrinkEnumHypTac
- Auto-tactic: No
- Post-tactic: Default
- Preference Display: Shrink Enumerated Set (Simplify)
- Interactive: No
- Proving Interface Display: negEnum <hypotheses names>
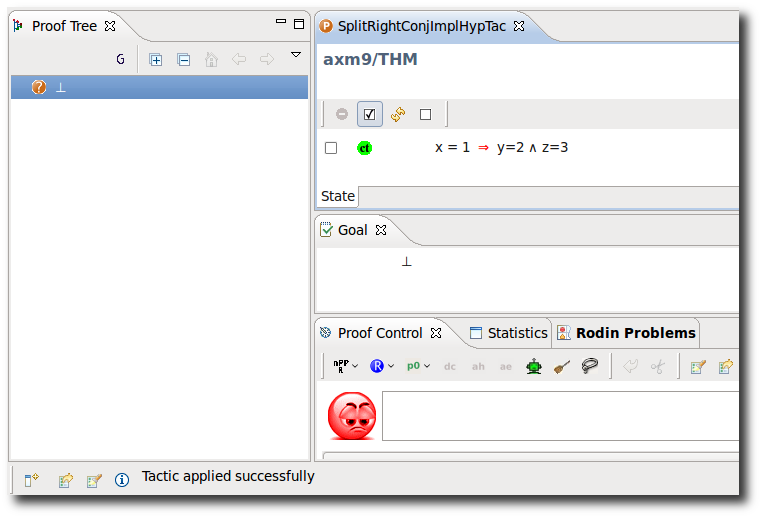
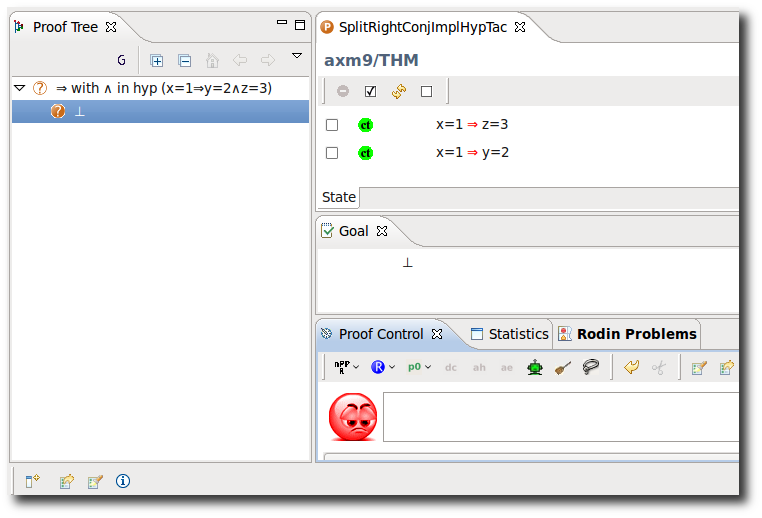
Implicative Hypothesis with Conjunctive RHS
- Description: Simplifies all (selected) hypotheses of the form P ⇒ Q ∧ R into multiple implications P ⇒ Q , P ⇒ R.
- Additional details:
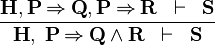
|
IMP_AND_L |
- ID: org.eventb.core.seqprover.splitRightConjImpHypTac
- Auto-tactic: No
- Post-tactic: Yes
- Preference Display: Implicative Hypotheses with Conjunctive RHS (Simplify)
- Interactive: Hypothesis
The operator ⇒ is redden in the hypotheses. When the mouse hovers the red symbol, the label of the tactic in the context menu is Implication with conjunction rewrites.
- Proving Interface Display: ⇒ with ∧ in hyp <hypothesis name>
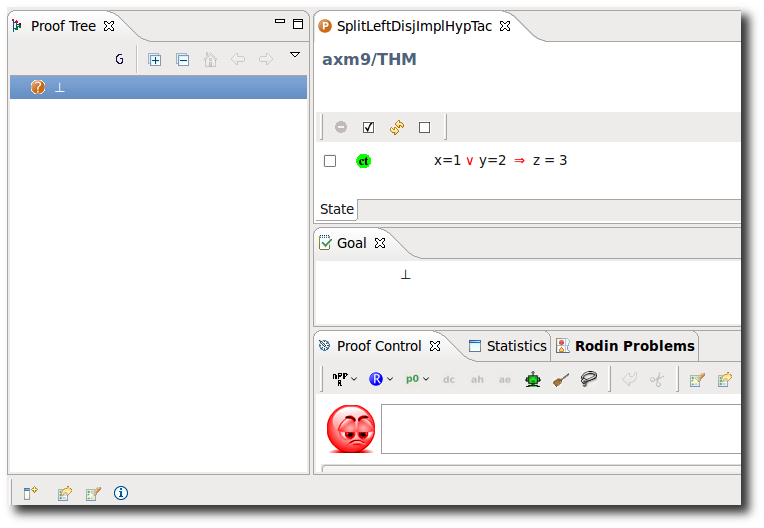
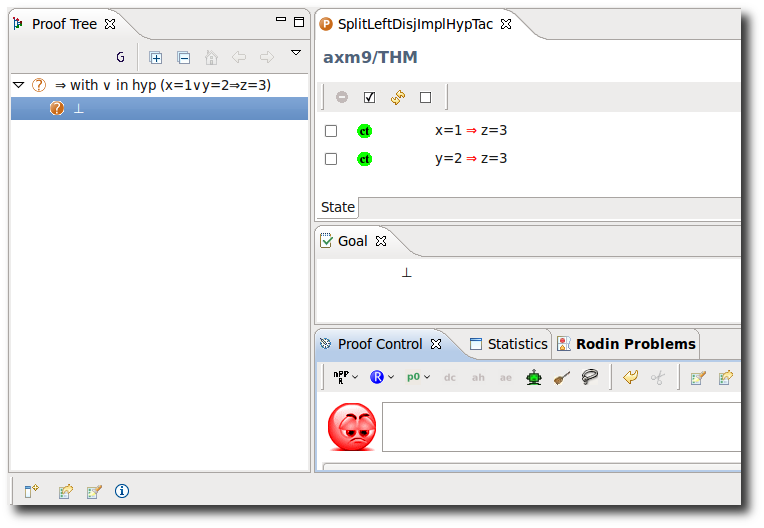
Implicative Hypothesis with Disjunctive LHS
- Description: Simplifies all (selected) hypotheses of the form P ∨ Q ⇒ R into multiple implications P ⇒ R , Q ⇒ R.
- Additional details:
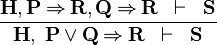
|
IMP_OR_L |
- ID: org.eventb.core.seqprover.splitLeftDisjImpHypTac
- Auto-tactic: No
- Post-tactic: Yes
- Preference Display: Implicative Hypotheses with Disjunctive LHS (Simplify)
- Interactive: Hypothesis
The operator ⇒ is redden in the hypotheses. When the mouse hovers the red symbol, the label of the tactic in the context menu is Implication with disjunction rewrites.
- Proving Interface Display: ⇒ with ∨ in hyp <hypothesis name>
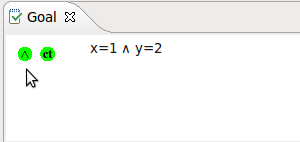
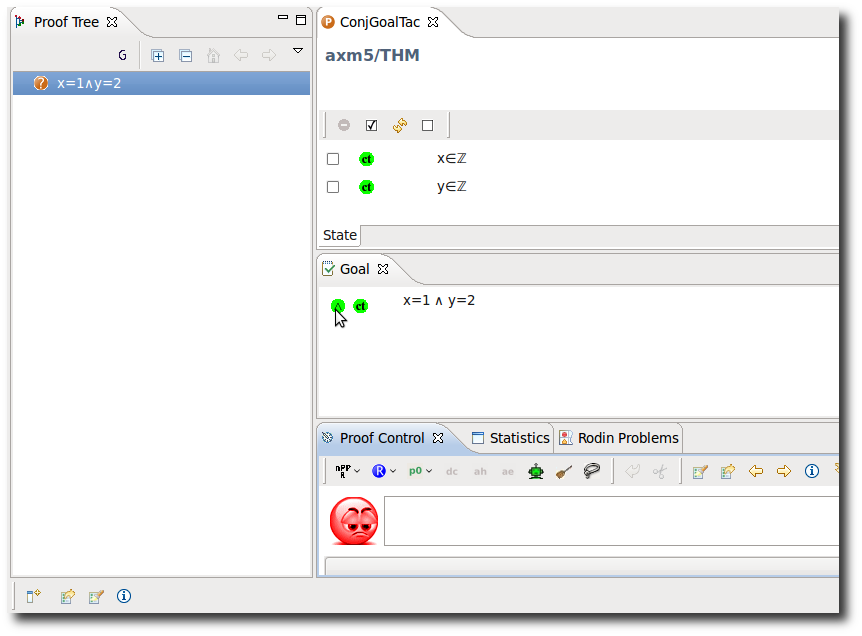
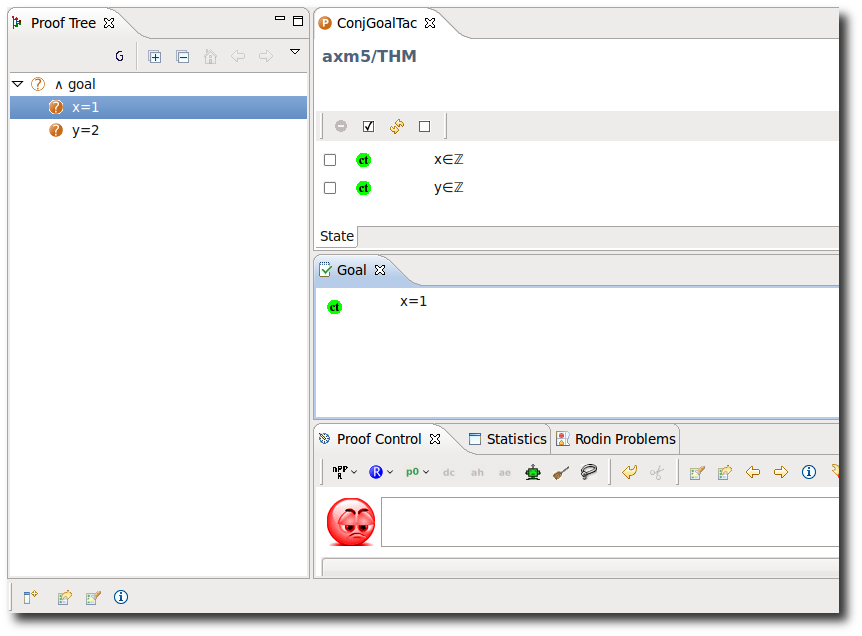
Conjunctive Goal
- Description: Splits a sequent with a conjunctive goal into multiple subgoals.
- Additional details:
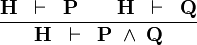
|
AND_R |
- ID: org.eventb.core.seqprover.conjGoalTac
- Auto-tactic: No
- Post-tactic: Yes
- Preference display: Conjunctive Goal (Split)
- Interactive: Goal
- Proving interface display: ∧ goal
The example below shows the screen-shots of the step before the application of the tactic and the step just after the application of the tactic.
Clarify Goal
- Description: Clarifies the goal by repeatedly by:
- splitting conjunctions,
- simplifying implications,
- simplifying universal quantifiers,
- discharging sequents with a true goal, a false hypothesis and where the goal is contained in the hypotheses.
- Additional details: This tactic applies a composition of tactics #Conjunctive Goal, #Implication Goal and #For-all Goal followed by a looping of tactics #True Goal and #False Hypothesis.
- ID: org.eventb.core.seqprover.clarifyGoalTac
- Auto-tactic: Default
- Post-tactic: Default
- Preference Display: Clarify Goal (Mixed)
- Interactive: No
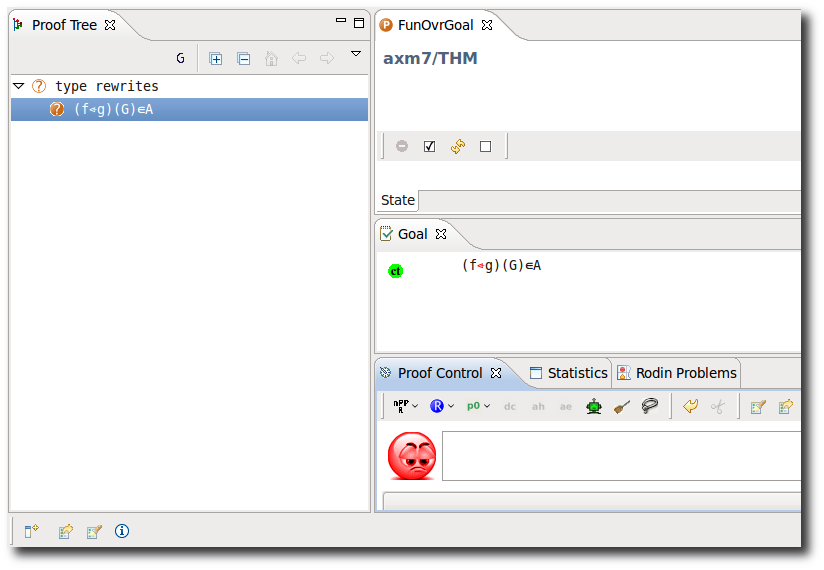
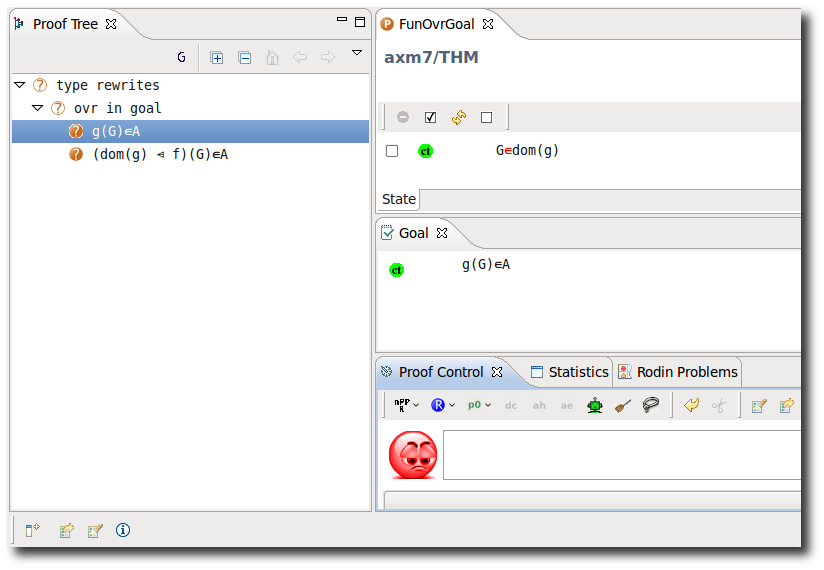
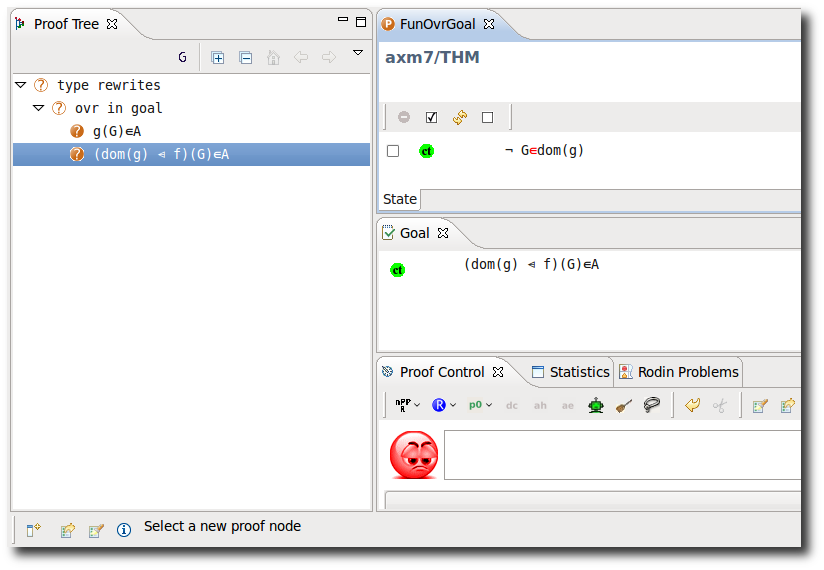
Functional Overriding in Goal
- Description: TODO
- Additional details:
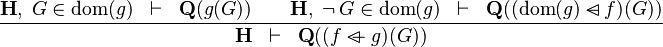
|
OV_R |
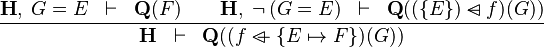
|
OV_SETENUM_R |
These inference rules are applied automatically, repeatedly and recursively.
- ID: org.eventb.core.seqprover.funOvrGoalTac
- Auto-tactic: Default
- Post-tactic: No
- Preference Display: Functional Overriding in Goal (Split)
- Interactive: Goal
When hovering the redden override operator <+, select (f<+{E|->F})(G) from the drop-down menu. (TODO strange menu item)
- Proving Interface Display: ovr in goal
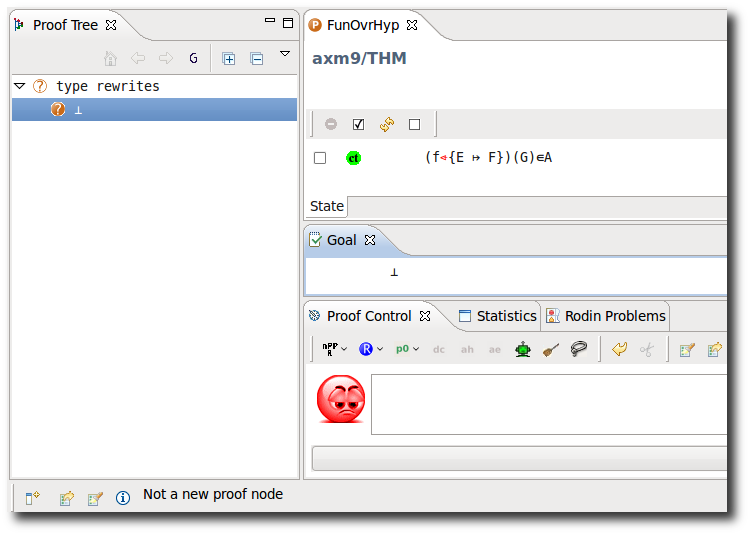
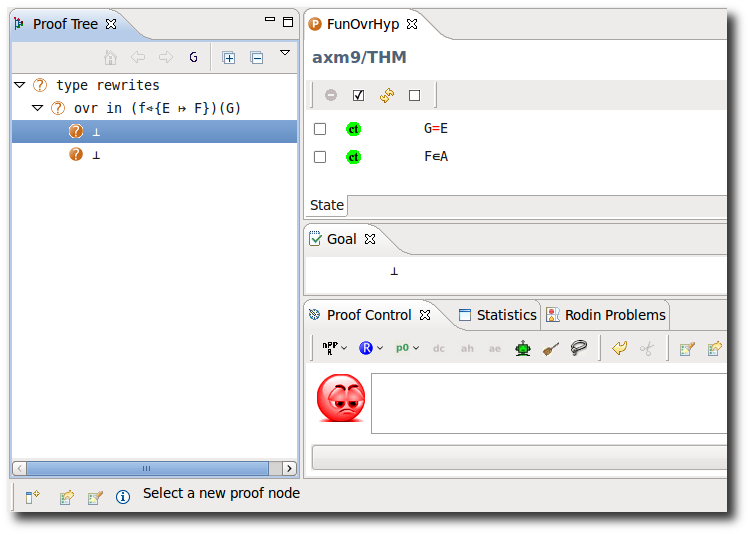
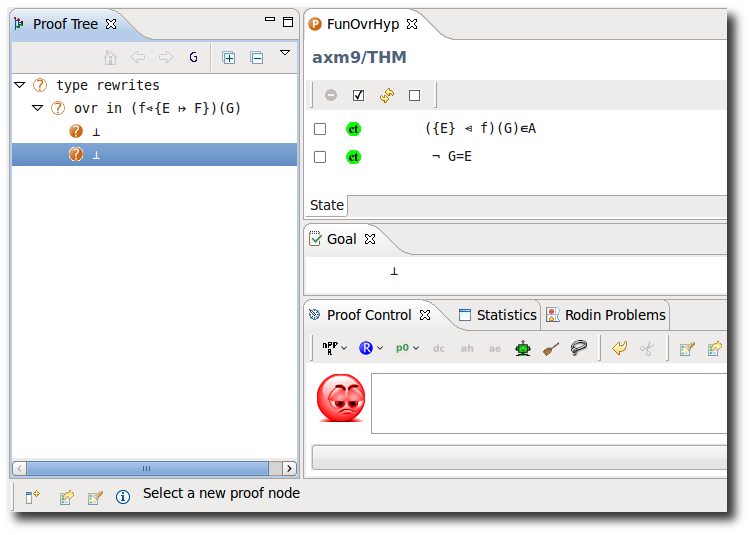
Functional Overriding in Hypothesis
- Description: TODO
- Additional details:
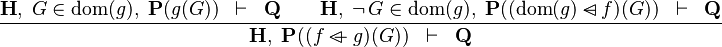
|
OV_L |
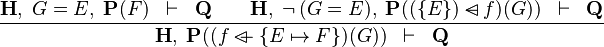
|
OV_SETENUM_L |
These inference rules are applied automatically, repeatedly and recursively.
- ID: org.eventb.core.seqprover.funOvrHypTac
- Auto-tactic: Yes
- Post-tactic: Yes
- Preference Display: Functional Overriding in Hypothesis (Split)
- Interactive: Hypothesis
When hovering the redden override operator <+, select (f<+{E|->F})(G) from the drop-down menu. (TODO strange menu item)
- Proving Interface Display: ovr in <hypothesis name>
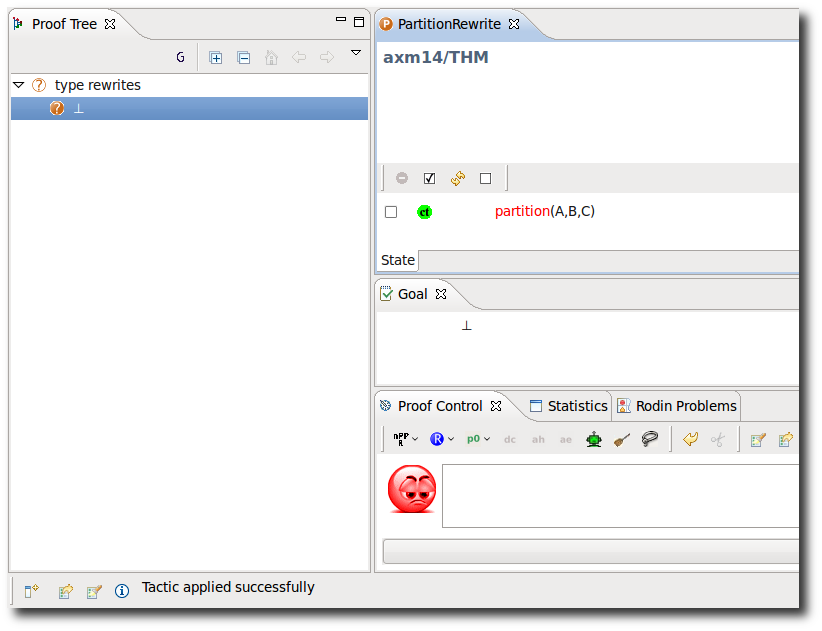
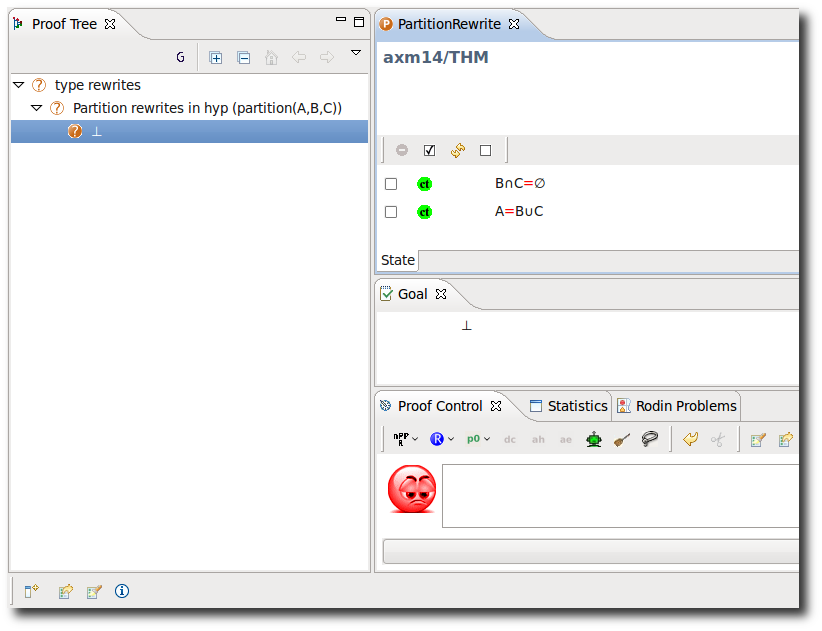
Partition Rewriter
- Description: Simplifies all predicates of the form partition(S, ...) into their expanded form in the goal and all visible hypotheses.
- Additional details: TODO
- ID: org.eventb.core.seqprover.partitionRewriteTac
- Auto-tactic: Default
- Post-tactic: No
- Preference Display: Partition Rewriter (Simplify)
- Interactive: Hypothesis, Goal
The predicate partition is redden in the goal or the hypotheses. When the mouse hovers the red symbol, the label of the tactic in the context menu is Rewrites a partition into its definition.
- Proving Interface Display: Partition rewrites in goal / hyp <hypothesis name>
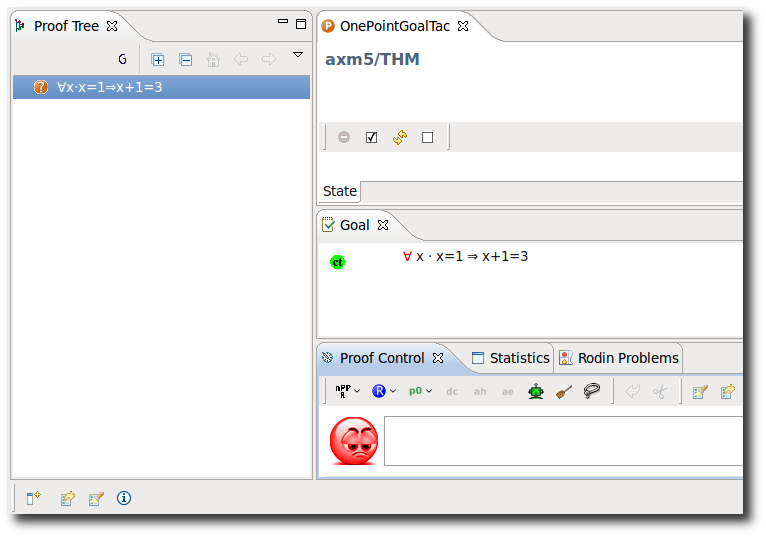
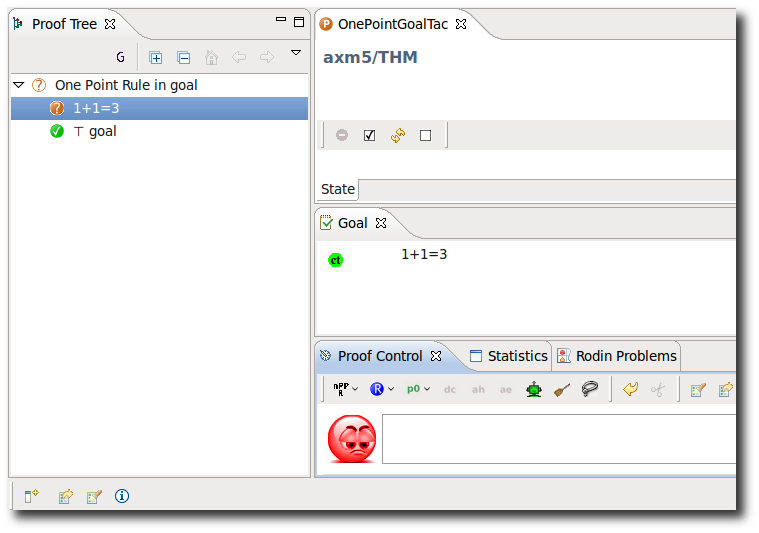
One-Point Rule in Goal
- Description: Applies automatically the OnePointGoal tactic to the goal.
- Additional details:
![\frac{\textbf{H} \;\;\vdash \;\; {WD}(E) \qquad \textbf{H} \;\;\vdash \;\; \forall x, \ldots, \ldots,z \qdot [y \bcmeq E]\textbf{P} \land \ldots \land \ldots \land [y \bcmeq E]\textbf{Q} \limp [y \bcmeq E]\textbf{R} }{ \textbf{H} \;\;\vdash\;\; \forall x, \ldots, y, \ldots, z \qdot \textbf{P} \land \ldots \land y = E \land \ldots \land \textbf{Q} \limp \textbf{R} }](/images/math/3/7/9/379ac43eaae96f14177427e9cbc89387.png)
|
ONE_POINT_R |
The rule can be applied with ∀ as well as with ∃.
- ID: org.eventb.core.seqprover.onePointGoalTac
- Auto-tactic: Yes
- Post-tactic: Yes
- Preference Display: One Point Rule in Goal (Split)
- Interactive: No
- Proving Interface Display: One Point Rule in goal
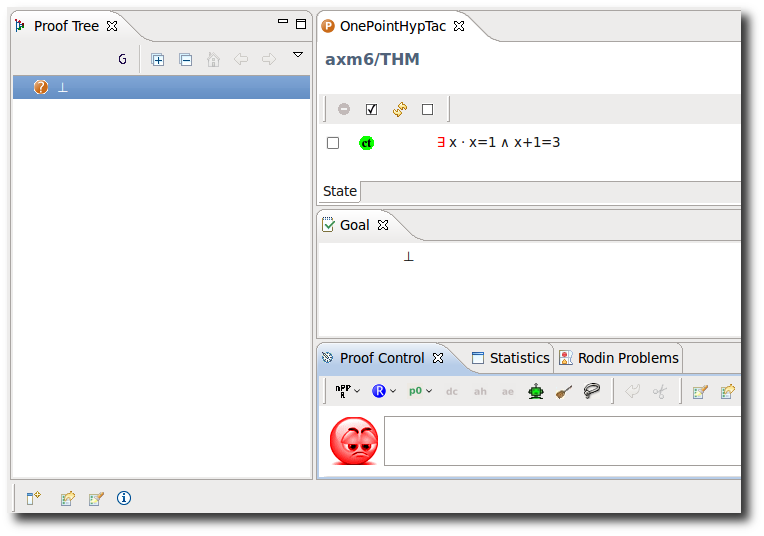
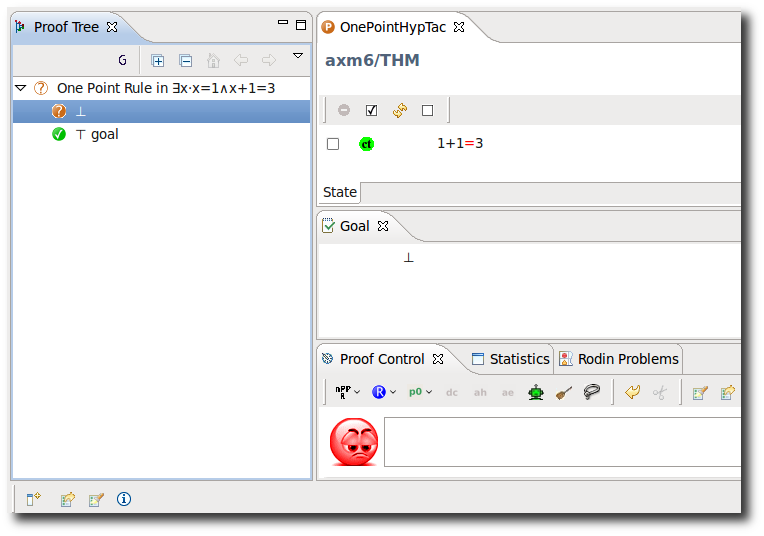
One-Point Rule in Hypothesis
- Description: Applies automatically the OnePointHyp tactic to the selected hypotheses.
- Additional details:
![\frac{\textbf{H} \;\;\vdash \;\; {WD}(E) \qquad \textbf{H}, \forall x, \ldots, \ldots,z \qdot [y \bcmeq E]\textbf{P} \land \ldots \land \ldots \land [y \bcmeq E]\textbf{Q} \limp [y \bcmeq E]\textbf{R} \;\;\vdash \;\; \textbf{G}}{ \textbf{H}, \forall x, \ldots, y, \ldots, z \qdot \textbf{P} \land \ldots \land y = E \land \ldots \land \textbf{Q} \limp \textbf{R} \;\;\vdash\;\; \textbf{G}}](/images/math/8/b/1/8b19ec24619d8d756596ebe54616be06.png)
|
ONE_POINT_L |
The rule can be applied with ∀ as well as with ∃.
- ID: org.eventb.core.seqprover.onePointHypTac
- Auto-tactic: Yes
- Post-tactic: Yes
- Preference Display: One Point Rule in Hypotheses (Split)
- Interactive: No
- Proving Interface Display: One Point Rule in hypothesis name
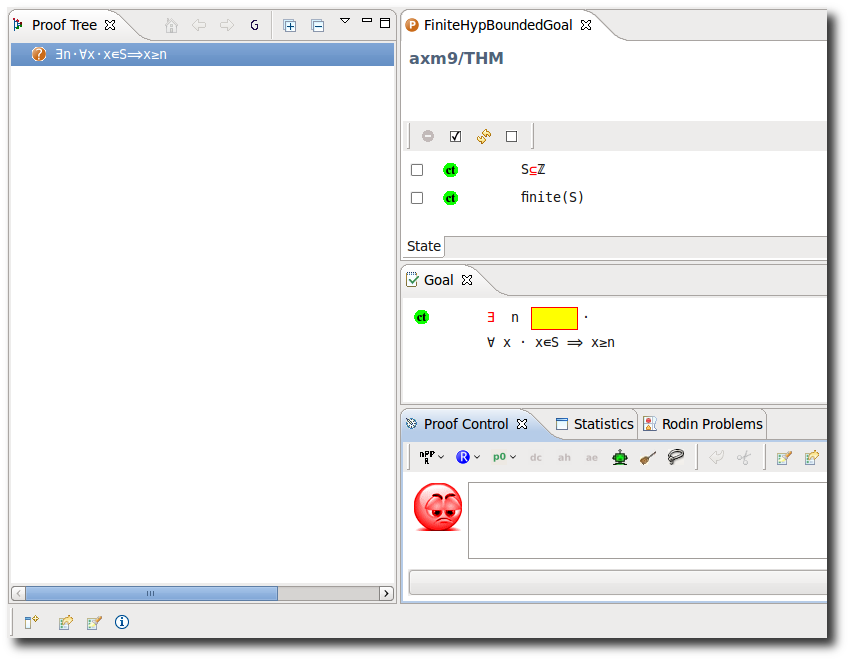
Bounded Goal with Finite Hypothesis
- Description: Discharges a sequent whose goal states that an expression E has a lower or a upper bound (e.g. ∃n·(∀x·x ∈ S ⇒ x ≤ n)), when there is an hypothesis that states the finiteness of E (i.e. finite(S)).
- Additional details:
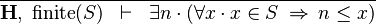
|
FIN_L_LOWER_BOUND_L |
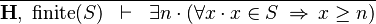
|
FIN_L_LOWER_BOUND_R |
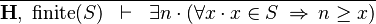
|
FIN_L_UPPER_BOUND_L |
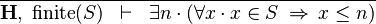
|
FIN_L_UPPER_BOUND_R |
- ID: org.eventb.core.seqprover.finiteHypBoundedGoalTac
- Auto-tactic: Default
- Post-tactic: Default
- Preference Display: Bounded Goal with finite Hypothesis (Discharge)
- Interactive: No
- Proving Interface Display: Existence of minimum or maximum in goal with finite hypothesis