Structured Types: Difference between revisions
imported>WikiSysop |
imported>WikiSysop |
||
| Line 9: | Line 9: | ||
{{SimpleHeader}} | {{SimpleHeader}} | ||
|<math> \begin{array}{lcl} | |<math> \begin{array}{lcl} | ||
\textbf{STRUCT}~~ C &::& e\in E\\ | \textbf{STRUCT}~~~~ C &::& e\in E\\ | ||
&& f \in F | && f \in F | ||
\end{array} | \end{array} | ||
Revision as of 15:59, 1 May 2009
Modelling Structured Types
The Event-B mathematical language currently does not support a syntax for the direct definition of structured types such as records or class structures. Nevertheless it is possible to model structured types using projection functions to represent the fields/ attributes. For example, suppose we wish to model a structured type C with fields e and f (with type E and F respectively). Let us use the following syntax for this (not part of Event-B):
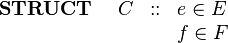
|
We can model this structure in Event-B by introducing (in a context) a set 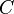 and two
functions
and two
functions  and
and 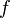 as constants as follows:
as constants as follows:
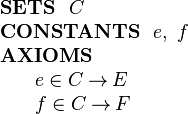
|
Names in the proof tree: Predicate Prover
Names in the preferences: PP restricted, PP after lasso, PP unrestricted
Input: In the configuration "restricted" all selected hypotheses and the goal are passed to New PP. In the configuration "after lasso" a lasso operation is applied to the selected hypotheses and the goal and the result is passed to New PP. The lasso operation selects any unselected hypothesis that has a common symbol with the goal or a hypothesis that was selected before. In the configuration "unrestricted" all the available hypotheses are passed to New PP.
How the Prover Proceeds: First, all function and predicate symbols that are different from "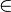 " and not related to arithmetic are translated away. For example
" and not related to arithmetic are translated away. For example 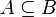 is translated to
is translated to 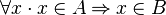 . Then New PP translates the proof obligation to CNF (conjunctive normal form) and applies a combination of unit resolution and the Davis Putnam algorithm.
. Then New PP translates the proof obligation to CNF (conjunctive normal form) and applies a combination of unit resolution and the Davis Putnam algorithm.
Some Strengths:
- New PP outputs a set of "used hypotheses". If an unused hypotheses changes, the old proof can be reused.
- New PP has limited support for equational reasoning.