Structured Types: Difference between revisions
imported>WikiSysop |
imported>WikiSysop |
||
| Line 180: | Line 180: | ||
==Sub-Typing== | ==Sub-Typing== | ||
Extension, as described above, is used when adding new fields to a structured type as part of a refinement step. | |||
That is, at different abstraction levels, we may have different numbers of fields in a structured type. | |||
Sometimes we wish to have different subtypes of a structure at the ''same'' abstraction level. | |||
We can achieve this by defining subset of the structure type and defining projection functions for those | |||
subsets only. For example suppose we define a message type that has sender and receiver fields as well | |||
as a message identifier. | |||
In our invented notation this would be: | |||
<center> | |||
{{SimpleHeader}} | |||
|<math> \begin{array}{lcl} | |||
\textbf{RECORD}~~~~ Message &::& sender\in Agent\\ | |||
&& receiver \in Agent \\ | |||
&& ident \in Ident | |||
\end{array} | |||
</math> | |||
|} | |||
</center> | |||
In Event-B this would be: | |||
<center> | |||
{{SimpleHeader}} | |||
|<math> \begin{array}{l} | |||
\textbf{SETS}~~ Message\\ | |||
\textbf{CONSTANTS}~~ sender,~ receiver, ident\\ | |||
\textbf{AXIOMS}\\ | |||
~~~~\begin{array}{l} | |||
sender \in Message \tfun Agent\\ | |||
receiver \in Message \tfun Agent\\ | |||
ident \in Message \tfun Ident | |||
\end{array} | |||
\end{array} | |||
</math> | |||
|} | |||
</center> | |||
We wish to have two subtypes of message, ''request'' messages and ''confirmation'' messages. | |||
We define two subsets of ''Message'' as follows: | |||
<center> | |||
{{SimpleHeader}} | |||
|<math> \begin{array}{l} | |||
\textbf{CONSTANTS}~~ \textit{ReqMessage},~ \textit{ConfMessage}\\ | |||
\textbf{AXIOMS}\\ | |||
~~~~\begin{array}{l} | |||
\textit{ReqMessage} \subseteq Message \\ | |||
\textit{ConfMessage} \subseteq Message \\ | |||
\end{array} | |||
\end{array} | |||
</math> | |||
|} | |||
</center> | |||
We require requests to have a product and an amount field and a confirmation to have a price field. | |||
In our invented notation this would be specified as follows: | |||
<center> | |||
{{SimpleHeader}} | |||
|<math> \begin{array}{l} | |||
\textbf{EXTEND~~ RECORD}~~ \textit{ReqMessage}~~\textbf{WITH}\\ | |||
~~~~~~~~~~~~ product\in Product\\ | |||
~~~~~~~~~~~~ amount\in \nat\\ | |||
\textbf{EXTEND~~ RECORD}~~ \textit{ConfMessage}~~\textbf{WITH}\\ | |||
~~~~~~~~~~~~ price\in \nat\\ \end{array} | |||
</math> | |||
|} | |||
</center> | |||
In Event-B the additional fields are specified as projection functions on the relevant message subsets: | |||
<center> | |||
{{SimpleHeader}} | |||
|<math> \begin{array}{l} | |||
\textbf{CONSTANTS}~~ product,~ amount, price\\ | |||
\textbf{AXIOMS}\\ | |||
~~~~\begin{array}{l} | |||
product \in \textit{ReqMessage} \tfun Product\\ | |||
amount \in \textit{ReqMessage} \tfun \nat\\ ~\\ | |||
price \in \textit{ConfMessage} \tfun \nat | |||
\end{array} | |||
\end{array} | |||
</math> | |||
|} | |||
</center> | |||
Typically we would require that the message subtypes are disjoint. In that case we would add and additional axiom: | |||
<center> | |||
{{SimpleHeader}} | |||
|<math> \begin{array}{l} | |||
\textbf{AXIOMS}\\ | |||
~~~~\begin{array}{l} | |||
\textit{ReqMessage} \cap \textit{ConfMessage} ~=~ \emptyset \\ | |||
\end{array} | |||
\end{array} | |||
</math> | |||
|} | |||
</center> | |||
If we know that theee are no other subtypes besides requests and confirmations and they should be disjoint, | |||
then we can condense subset and disjointness axioms into a partitions axiom: | |||
<center> | |||
{{SimpleHeader}} | |||
|<math> \begin{array}{l} | |||
\textbf{AXIOMS}\\ | |||
~~~~\begin{array}{l} | |||
partition(~ Message, ~\textit{ReqMessage},~ \textit{ConfMessage} ~) | |||
\end{array} | |||
\end{array} | |||
</math> | |||
|} | |||
</center> | |||
==Recursive Structured Types== | ==Recursive Structured Types== | ||
==Structured Variables== | ==Structured Variables== | ||
Revision as of 17:21, 5 May 2009
Modelling Structured Types
The Event-B mathematical language currently does not support a syntax for the direct definition of structured types such as records or class structures. Nevertheless it is possible to model structured types using projection functions to represent the fields/attributes. For example, suppose we wish to model a record structure R with fields e and f (with type E and F respectively). Let us use the following syntax for this (not part of Event-B syntax):
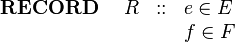
|
We can model this structure in Event-B by introducing (in a context) a carrier set R and two functions e and f as constants as follows:
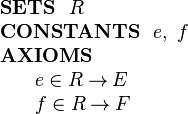
|
The (constant) functions e and f are projection functions that can be used to extract the appropriate field values.
That is, given an element 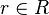 representing a record structure, we write
representing a record structure, we write 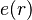 for the e component of r and
for the e component of r and 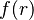 for the f component of r.
for the f component of r.
E and F can be any type definable in Event-B, including a type representing a record structure.
The approach to modelling structured types is based on a proposal by Evans and Butler [1].
Constructing Structured Values
Suppose we have a variable v in a machine whose type is the structure R defined above:
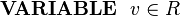
We wish to assign a structured value to v whose e field has some value e1 and whose f field has some value f1. This can be achieved by specifying the choice of an event parameter r whose fields are constrained by appropriate guards and assigning parameter r to the machine variable v. This is shown in the following event:
![Ev1 ~=\begin{array}[t]{l}
\textbf{ANY}~~ r ~~\textbf{WHERE} \\
~~~~ r \in R \\
~~~~ e( r ) = e1 \\
~~~~ f( r ) = f1 \\
\textbf{THEN} \\
~~~~ v := r \\
\textbf{END}
\end{array}](/images/math/c/0/a/c0acb8ea42c896a857cb486bf58e89c5.png)
If we only wish to update some fields and leave others changed, this needs to be done by specifying explicitly that some fields remain unchanged. This is shown in the following example where only the e field is modified:
![Ev2 ~=\begin{array}[t]{l}
\textbf{ANY}~~ r ~~\textbf{WHERE} \\
~~~~ r \in R \\
~~~~ e( r ) = e1 \\
~~~~ f( r ) = f(v) \\
\textbf{THEN} \\
~~~~ v := r \\
\textbf{END}
\end{array}](/images/math/b/4/b/b4b0c62e8c2f0b200e0b603baffe0232.png)
If we don't care about the value of some field (e.g., f), we simply omit any guard on that field as follows:
![Ev3 ~= \begin{array}[t]{l}
\textbf{ANY}~~ r ~~\textbf{WHERE} \\
~~~~ r \in R \\
~~~~ e( r ) = e1 \\
\textbf{THEN} \\
~~~~ v := r \\
\textbf{END}
\end{array}](/images/math/1/6/0/16084255bc2a039f74d290d8f445e8ed.png)
Sometimes we will wish to model a set of structured elements as a machine variable, e.g.,
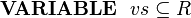
We can add a structured element to this set using the following event:
![AddElement ~=
\begin{array}[t]{l}
\textbf{ANY}~~ r ~~\textbf{WHERE} \\
~~~~ r \in R \\
~~~~ e( r ) = e1 \\
~~~~ f( r ) = f1 \\
\textbf{THEN} \\
~~~~ vs := vs \cup \{r\} \\
\textbf{END}
\end{array}](/images/math/8/9/5/895f1186bc2e29ebdcac258ad8b929b1.png)
Extending Structured Types
In a refinement we can introduce new fields to an existing structured type. Suppose R is defined in context C1 with fields e and f as before. For the refinement, suppose we wish to add a field g of type G to structured type R. Let us use the following syntax for this (not part of Event-B syntax):
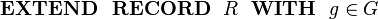
|
This can be including the new field g as projection function on R in a context C2 (that extends C1). The new field is defined as follows:
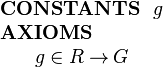
|
Above, we saw the AddElement event that adds a structured element to the set vs. We may want to specify a value for the new g field in the refinement of this event. Using the event extension mechanism, this can be achieved as follows:
![AddElement~= \begin{array}[t]{l}
\textbf{EXTENDS}~~ AddElement \\
\textbf{WHEN} \\
~~~~ g( r ) = g1 \\
\textbf{THEN} \\
~~~~ skip \\
\textbf{END}
\end{array}](/images/math/e/c/4/ec4898896eebca6d817c466fcd201b9b.png)
The event extension mechanism means that this short form is the same as specifying the refined event as follows:
![AddElement ~=
\begin{array}[t]{l}
\textbf{REFINES}~~ AddElement \\
\textbf{ANY}~~ r ~~\textbf{WHERE} \\
~~~~ r \in R \\
~~~~ e( r ) = e1 \\
~~~~ f( r ) = f1 \\
~~~~ g( r ) = g1 \\
\textbf{THEN} \\
~~~~ vs := vs \cup \{r\} \\
\textbf{END}
\end{array}](/images/math/a/0/2/a02af36631152aeb174233bd77b56b58.png)
Sub-Typing
Extension, as described above, is used when adding new fields to a structured type as part of a refinement step. That is, at different abstraction levels, we may have different numbers of fields in a structured type.
Sometimes we wish to have different subtypes of a structure at the same abstraction level. We can achieve this by defining subset of the structure type and defining projection functions for those subsets only. For example suppose we define a message type that has sender and receiver fields as well as a message identifier. In our invented notation this would be:
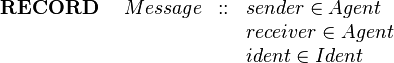
|
In Event-B this would be:

|
We wish to have two subtypes of message, request messages and confirmation messages. We define two subsets of Message as follows:
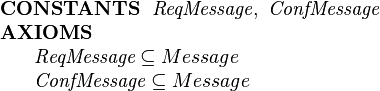
|
We require requests to have a product and an amount field and a confirmation to have a price field.
In our invented notation this would be specified as follows:

|
In Event-B the additional fields are specified as projection functions on the relevant message subsets:
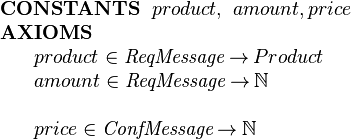
|
Typically we would require that the message subtypes are disjoint. In that case we would add and additional axiom:
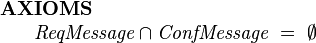
|
If we know that theee are no other subtypes besides requests and confirmations and they should be disjoint, then we can condense subset and disjointness axioms into a partitions axiom:
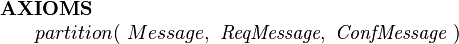
|