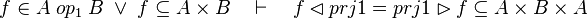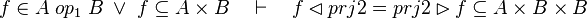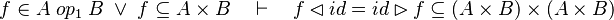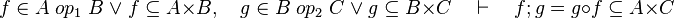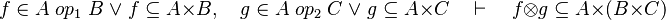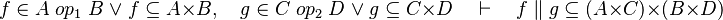Membership in Goal: Difference between revisions
imported>Billaude No edit summary |
imported>Billaude |
||
| Line 62: | Line 62: | ||
#*<math>ran(f)\cup ran(g)\subseteq ran(f\ovl g)</math> | #*<math>ran(f)\cup ran(g)\subseteq ran(f\ovl g)</math> | ||
#*<math>dom(A\domres f) = dom(f)\cap A</math> | #*<math>dom(A\domres f) = dom(f)\cap A</math> | ||
#*<math>ran(f\ranres A) = ran(f)\cap A</math> | #*<math>ran(f\ranres A) = ran(f)\cap A</math> | ||
#*<math>f\in A\;op_1\;B\;\lor\; f\subseteq A\cprod B\quad\vdash\quad f\subseteq A\cprod B</math> | #*<math>f\in A\;op_1\;B\;\lor\; f\subseteq A\cprod B\quad\vdash\quad f\subseteq A\cprod B</math> | ||
#*<math>f\in A\;op_1\;B\;\lor\; f\subseteq A\cprod B\quad\vdash\quad f^{-1}\subseteq B\cprod A</math> | #*<math>f\in A\;op_1\;B\;\lor\; f\subseteq A\cprod B\quad\vdash\quad f^{-1}\subseteq B\cprod A</math> | ||
Revision as of 07:57, 30 June 2011
Objective
This page describes the design of the reasoner MembershipGoal and its associated tactic MembershipGoalTac.
This reasoner discharges sequent whose goal denotes a membership which can be inferred with hypotheses. Here an basic example of what it discharges :
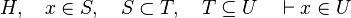
Analysis
Such sequent are proved by PP and ML. But, these provers have both drawbacks :
- All the visible are added as needed hypotheses, which is most of the time not the case.
- They take quite consequent time to prove it (even with the basic example given here above, the difference in time execution is noticeable).
- If there are too many hypotheses, or if the expression of the
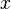 is too complicated, they may not prove it.
is too complicated, they may not prove it.
This is particularly true when in the list of inclusion expressions of each side of the relation are not equal. For example : 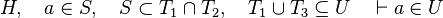
Such a reasoner contributes to prove more Proof Obligations automatically, faster and with fewer needed hypotheses which makes proof rule more legible and proof replay less sensitive to modifications.
Tactic
This part explains how the tactic (MembershipGoalTac) associated to the reasoner MembershipGoal is working.
Goal
The tactic (as the reasoner) should works only on goals such as :
For example those examples matches with the definition here above :
Every other goals denoting a membership should be re-
Hypotheses
The hard part is to find the hypotheses leading to discharge the sequent. To do so, the tactic recovers three kinds of hypotheses :
- the ones related to the left member of the goal
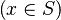 (this is the start point):
(this is the start point):
- the ones denoting inclusion (all but the ones matching the description of the first point) :
- the one from which we can infer inclusion :
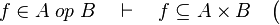 where
where  is one of :
is one of :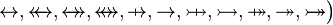
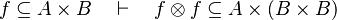
Then, it will search a link between those hypotheses so that the sequent can be discharged.
Find a path
Now that we recovered all the hypotheses that could be useful for the reasoner, it just remains to find a path among the hypotheses leading to discharge the sequent. Depending on the relations on each side of the inclusion, we will act differently. 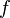 always represent an expression (may be a domain, a range, etc.).
always represent an expression (may be a domain, a range, etc.).
- The following sequent is provable because
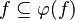 .
.
- The following sequent is provable because
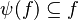 .
.
- We can generalized the first two points. This is the Russian dolls system. We can easily prove a sequent with multiple inclusions by going from hypothesis to hypothesis.
- For some relations, positions are needed to be known to continue to find hypotheses, but it is not always necessary.
- Those rewrites can be useful when the Russian dolls system does not succeed.
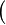 where
where 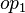 and
and 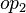 are ones of :
are ones of :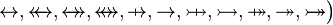
By using these inclusion and rewrites, it tries to find a path among the recovered hypotheses. Every hypotheses denoting an inclusion should be used only once. Every hypotheses from which new hypothesis can be inferred could be used as many times as wanted. Among all paths that lead to discharge the sequent, the tactic give the first it finds. Moreover, so that the reasoner does not do the same work as the tactic of writing new hypothesis, it gives all needed hypotheses and added hypotheses in the input.
Reasoner
This part describes how the reasoner works.
Goal
The goal must match the same kind of goal as describes in the tactic part.
Input
Because we do not want to do the job of re-writing, every added hypotheses used to discharge the sequent should be contained in the input (the reasoner must extend HypothesesReasoner) as well as hypotheses used to perform the re-writing and hypotheses used to discharge the sequent. Thus we get those obligations :
- Every added hypotheses must be re-writable with hypotheses contained in the sequent and in the input.
- Every added hypotheses should be used to discharge the sequent.
- Hypotheses used to perform re-writing could be also used to discharge a sequent and may be used several times to prove that added hypotheses are re-writable.
- Hypotheses used to discharge the sequent should be used only once in the path (no loop allowed).
- It checks that with all these hypotheses can actually discharge the sequent
If all those tests pass, then the sequent is discharged. The added hypotheses are set as AddedHyps, and all the other hypotheses of the input are set as NeededHps.
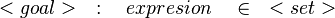
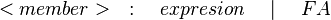
![<set>\quad:\quad expresion\otimes expresion\quad\mid\quad expresion\parallel expresion\quad\mid\quad <union>\quad\left[\cup <union>\right]](/images/math/5/2/7/52716b854ca9d6957fb9a1aba0c2fbed.png)
![<union>\quad:\quad<cprod>\quad\left[\cprod<cprod>\right]](/images/math/4/8/8/488b043c8999faf9503ba1f02d3a6444.png)
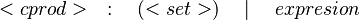
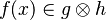
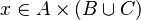
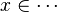
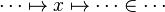
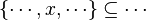
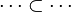
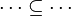
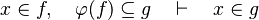

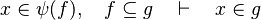

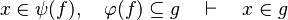
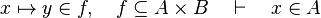
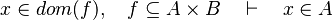
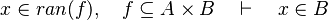
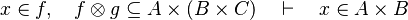
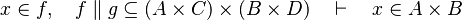
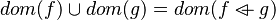
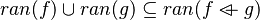
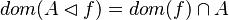
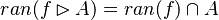
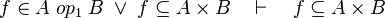
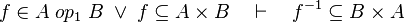
![f\in A\;op_1\;B\;\lor\; f\subseteq A\cprod B\quad\vdash\quad f[A]\subseteq B](/images/math/d/0/f/d0f87e70ea31bc0378c96cb36a9b3453.png)