Difference between pages "Proof Manager" and "The Use of Theories in Code Generation"

From Event-B
(Difference between pages)
Jump to navigationJump to search
imported>Son
 
imported>Andy
 
Line 1: Line 1:
−
The Proof Manager is responsible for constructing proofs and maintaining existing proofs associated with proof obligations.
+
= Defining Translations Using The Theory Plug-in =
 +
The theory plug-in is used to add mathematical extensions to Rodin. The theories are created, and deployed, and can then be used in any models in the workspace. When dealing with implementation level models, such as in Tasking Event-B, we need to consider how to translate newly added types and operators into code. We have augmented the theory interface with a Translation Rules section. This enables a user to define translation rules that map Event-B formulas to code.
 +
== Translation Rules==
 +
<div id="fig:Translation Rules">
 +
<br/>
 +
[[Image:TheoryCGRules.png|center||caption text]]
 +
<center>'''Figure 1''': Translation Rules</center>
 +
<br/>
 +
</div>
  
−
== Overview ==
+
Figure 1 shows the interface, and some translations rules of the mapping to Ada.
  
−
Proof obligations are generated by the proof obligation generator and have the form of ''[[Proof Manager#Sequents|sequents]]''.
+
The theory is given a name, and may import some other theories. Type parameters can be added, and we use them here to type the meta-variables. The meta-variable ''a'' is restricted to be an integer type, but meta-variable ''c'' can be any type. Meta-variables are used in the translator rules for pattern matching.
  
−
Sequents are proved using ''[[Proof Manager#Proof Rules|proof rules]]''.
+
Translator rules are templates, which are used in pattern matching. Event-B formulas are defined on the left hand side of the rule, and the code to be output (as text) appears on the right hand side of the matching rule. During translation an abstract syntax tree (AST) representation of the formula is used. The theory plug-in attempts to match the formulas in the rules with each syntactic element of the AST. As it does so it builds the textual output as a string, until the whole AST has been successfully matched. When a complete tree is matched, the target code is returned. If the AST is not matched, a warning is issued, and a string representation of the original formula is returned.
  
−
The Proof Manager architecture is separated into two parts: ''extensible'' part and ''static'' part. The extensible part is responsible for generating individual proof rules. The static part is responsible for putting proof rules together to construct and manage proofs. We call components that generate valid proof rules ''[[Proof Manager#Reasoners|reasoners]]''.
+
== Type Rules for Code Generation ==
  
−
The basic reasoning capabilities of the Proof Manager can be extended by adding new reasoners. A reasoner may implement a decision procedure for automated proof, or a derived rule schema for interactive proof.
+
The type rules section, shown in Figure 1, is where the relationship is defined, between Event-B types and the type system of the implementation.
  
−
By applying the generated proof rules by different reasoner, the Proof Manager builds a (partial) proof for an proof obligation by constructing ''[[Proof Manager#Proof Trees|proof trees]]''.
+
= Adding New (implementation-level) Types =
 +
When we are working at abstraction levels close to the implementation level, we may make an implementation decision which requires the introduction of a new type to the development. We give an example of our approach, where we add a new array type, shown in Figure 2, and then define its translation to code.
  
−
In order to encapsulate frequently used proof construction and manipulation steps, the Proof Manager provides the concept of ''[[Proof Manager#Tactics|tactics]]''. They provides high-level strategic proof manipulations. Adding new tactics is the second possibility for extending the Proof Manager.
+
== An Array Type Definition ==
 +
<div id="fig:Extension with an Array Type">
 +
<br/>
 +
[[Image:ArrayDef.png|center||caption text]]
 +
<center>'''Figure 2''': Array Definition</center>
 +
<br/>
 +
</div>
  
−
== Sequents ==
+
The array operator notation is defined in the expression array(s: P(T)); and the semantics is defined in the direct definition. arrayN constrains the arrays to be of fixed length. Array lookup, update, and constructor operators are subsequently defined. In the next step we need to define any translations required to implement the array in code.
−
A sequent stands for something we want to prove.
 
  
−
Sequents are of the following form
+
== Translation Rules ==
  
−
<math>H \vdash G</math>
+
<div id="Translation Rules for the Array Type">
 +
<br/>
 +
[[Image:ArrayTrans.png|center||caption text]]
 +
<center>'''Figure 3''': Translation Rules for the Array Type</center>
 +
<br/>
 +
</div>
  
−
where '''H''' is the set of hypotheses (predicates) and '''G''' is the goal (a predicate in the mathematical language).
+
Figure 3 shows the Ada translation; beginning with the meta-variable definitions that are used for pattern matching in the translation rules. Each of the operators; ''newArray'', and ''update'', and an expression using the ''lookup'' operator, are mapped to their implementations on the right hand side of the rule. The ''Type Rules'' section describes the implementation's description of the ''arrayN'' type.
−
 
 
−
The meaning of the above sequent is that: ''Under the hypotheses H, prove the goal G''.
 
−
 
 
−
== Proof Rules ==
 
−
In its pure mathematical form, a proof rule is a tool to perform formal proof and is denoted by:
 
−
 
 
−
{{InfRule||<math>\frac{\quad A\quad}{C}</math>}}
 
−
 
 
−
where '''A''' is a (possibly empty) list of sequents:the antecedents of the proof rule; and '''C''' is a sequent: the consequent of the rule. And we interpret the above proof rule as follows: The proofs of each sequent of '''A''' together give a proof of sequent '''C'''.
 
−
 
 
−
=== Representation ===
 
−
In Rodin, the representation for proof rules are more structure not only to reduce the space required to store the rule, but more importantly to support proof reuse.
 
−
 
 
−
A rule in Rodin contains the following:
 
−
 
 
−
* '''used goal''' A used goal predicate.
 
−
 
 
−
* '''used hypotheses''' The set of used hypotheses.
 
−
 
 
−
* '''antecedents''' A list of antecedents (to be explain later).
 
−
 
 
−
* '''reasoner''' the reasoner used to generate this proof rule (See [[reasoners]]).
 
−
 
 
−
* '''reasoner input''' the input to the reasoner to generate this proof rule (See [[reasoners]]).
 
−
 
 
−
Each antecedent of the proof rule contains the following information:
 
−
 
 
−
* '''new goal''' A new goal predicate.
 
−
 
 
−
* '''added hypotheses''' The set of added hypotheses.
 
−
 
 
−
With this representation, a proof rule in Rodin corresponding to a proof schema as follows:
 
−
 
 
−
<math>
 
−
  \begin{array}{c}
 
−
    H, H_u, H_{A_0} \vdash G_{A_0} ~~~\ldots~~~ H, H_u, H_{A_0} \vdash G_{A_0} \\
 
−
    \hline
 
−
    H, H_u \vdash G_u
 
−
  \end{array}
 
−
</math>
 
−
 
 
−
Where:
 
−
 
 
−
* <math>H_u</math> is the set of used hypotheses
 
−
 
 
−
* <math>G_u</math> is the used goal
 
−
 
 
−
* <math>H_{A_i}</math> is the set of added hypotheses corresponding to the ith antecedent.
 
−
 
 
−
* <math>G_{A_i}</math> is the new goal corresponding to the ith antecedent.
 
−
 
 
−
* <math>H</math> is the meta-variable that can be instantiated.
 
−
 
 
−
=== Applying Proof Rules ===
 
−
Given a proof rule of the form mentioned above, the following describes how to apply this rule to an input ''sequent''. The result of this process is a list of output sequents if successful or ''null'' otherwise.
 
−
 
 
−
* The rule is applicable if the goal of the sequent is not exactly the same as the ''used goal'' or any of the ''used hypotheses'' is not contained in the set of hypotheses of the input sequent.
 
−
 
 
−
* In the case of applicable, the antecedent sequents are returned. The goal of each antecedent sequent is the ''new goal'' correspondingly.  The hypotheses of each antecedent sequent is the union of the old hypotheses and ''added hypotheses'' of the corresponding antecedent.
 
−
 
 
−
== Reasoners ==
 
−
 
 
−
== Proof Trees ==
 
−
 
 
−
== [[Tactics ==
 
−
 
 
−
[[Category:Developer documentation]]
 
−
[[Category:Rodin Platform]]
 

Revision as of 15:51, 15 May 2012

Defining Translations Using The Theory Plug-in

The theory plug-in is used to add mathematical extensions to Rodin. The theories are created, and deployed, and can then be used in any models in the workspace. When dealing with implementation level models, such as in Tasking Event-B, we need to consider how to translate newly added types and operators into code. We have augmented the theory interface with a Translation Rules section. This enables a user to define translation rules that map Event-B formulas to code.

Translation Rules


caption text
Figure 1: Translation Rules


Figure 1 shows the interface, and some translations rules of the mapping to Ada.

The theory is given a name, and may import some other theories. Type parameters can be added, and we use them here to type the meta-variables. The meta-variable a is restricted to be an integer type, but meta-variable c can be any type. Meta-variables are used in the translator rules for pattern matching.

Translator rules are templates, which are used in pattern matching. Event-B formulas are defined on the left hand side of the rule, and the code to be output (as text) appears on the right hand side of the matching rule. During translation an abstract syntax tree (AST) representation of the formula is used. The theory plug-in attempts to match the formulas in the rules with each syntactic element of the AST. As it does so it builds the textual output as a string, until the whole AST has been successfully matched. When a complete tree is matched, the target code is returned. If the AST is not matched, a warning is issued, and a string representation of the original formula is returned.

Type Rules for Code Generation

The type rules section, shown in Figure 1, is where the relationship is defined, between Event-B types and the type system of the implementation.

Adding New (implementation-level) Types

When we are working at abstraction levels close to the implementation level, we may make an implementation decision which requires the introduction of a new type to the development. We give an example of our approach, where we add a new array type, shown in Figure 2, and then define its translation to code.

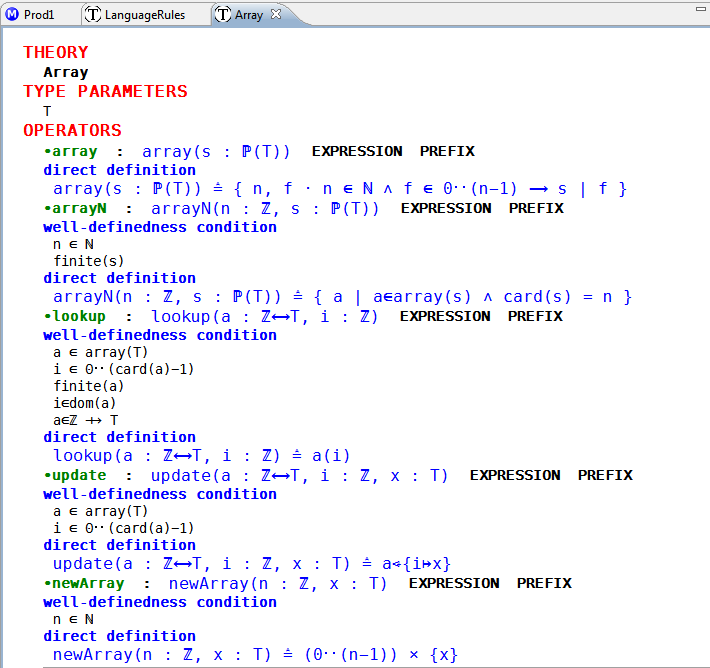
An Array Type Definition


caption text
Figure 2: Array Definition


The array operator notation is defined in the expression array(s: P(T)); and the semantics is defined in the direct definition. arrayN constrains the arrays to be of fixed length. Array lookup, update, and constructor operators are subsequently defined. In the next step we need to define any translations required to implement the array in code.

Translation Rules


caption text
Figure 3: Translation Rules for the Array Type


Figure 3 shows the Ada translation; beginning with the meta-variable definitions that are used for pattern matching in the translation rules. Each of the operators; newArray, and update, and an expression using the lookup operator, are mapped to their implementations on the right hand side of the rule. The Type Rules section describes the implementation's description of the arrayN type.

Retrieved from ‘https://wiki.event-b.org/index.php?title=Proof_Manager&oldid=10253’