ADVANCE D3.2 Model Checking

Overview

We think that animation and model checking are important tools when building a model. Animation allows the user to validate if the model corresponds to the user's intentions. Model checking allows to check if the model contains errors and provides counter-examples that help to understand the problem beforehand. Moreover, it allows to reason with domains (like physical units) and verify some properties (like temporal logic ones), that have currently no matching proof support.

The following activities were pursued within the project:

• The constraint solving capabilities of ProB have been continuously improved along with scalability improvements.

• A conversion from TLA to B has been added. ProB now supports TLA+. The motivation is to extend the reach of the project and to learn from TLA concerning certain features relevant for cyber-physical systems (e.g. real number support).

• There is work in progress towards full support of Theory plug-in: support for external and recursive functions has been added.

• The conversion to the relational logic solver Kodkod has been completed and experiments with Kodkod and SMT translators have been conducted.

• We are working on an analysis of the use of physical units in a formal model.

• We improved the usability of the LTL model checker.

• Regarding BMotion Studio, we focused on fixing identified bugs and rectifying usability issues.

Motivations / Decisions

Improvements to Constraint-Solving
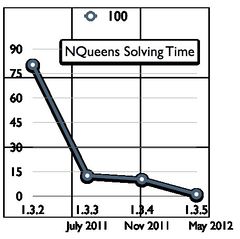
ProB's constraint solving capabilities are at the core of many of ProB's features: animation of high-level models with complicated predicates, model-based testing, constraint-based invariant and deadlock checking, etc. It is thus important to improve this aspect of ProB. In particular, we have continuously improved the performance of the kernel, as can be seen in the figure below showing the performance of ProB (in seconds) on the N-Queens problem for 100 queens. Other improvements lie in better expansion of universal and existential quantifiers, reification for the the bool operator and support for infinite and recursive functions. The latter is particularly important in light of the Theory plug-in work.

TLA2B
TLA+ and B share the common base of predicate logic, arithmetic and set theory. However, there are still considerable differences, such as very different approaches to typing and modularization. Some features of TLA+ are interesting in the context of cyber-physical systems, such as real numbers. There is also considerable difference in the available tool support. In particular, we wanted to compare ProB with TLC and gain insights about performance.

Physical Units
Formal models of cyber physical systems will contain variables which represent values with physical units. We are thus exploring to use the ProB model checker as a tool to infer and validate physical units usage in formal models. In particular, we want to make sure that the physical units in a model are used in a consistent way.

Theory Plug-in and Mathematical Extensions
In the ProB core, we have improved ProB to better deal with infinite and recursive functions. This can be used to provide formal specifications for mathematical extensions which can be animated and model checked by ProB. Using the newly developed external function mechanism, it should also be possible to support floats or reals, which will be important for certain cyber-physical systems.
On the technical side, we have extended the ProB internal representation of predicates and expressions to support the Theory plug-in. The implementation will be finalize as the Theory plug-in will allow access to definitions will be granted to ProB.

Kodkod
We have integrated a translation of B predicates to the relational logic solver "Kodkod" and evaluated how ProB's constraint solving compares to Kodkod's SAT solving. The integration allows to apply SAT solving to predicates where a translation is possible and a fallback to constraint solving for the remaining predicates. Our experiments have shown that the translation can be highly beneficial for certain kinds of constraints, and as such opens up new ways to analyze and validate formal specifications in Event-B. However, the experiments have also shown that the constraint logic programming approach of ProB can be superior in a considerable number of scenarios; the translation to Kodkod and down to SAT is not (yet) the panacea. The same can be said of the existing translations from B to SMT. As such, we believe that much more research required to reap the best of both worlds (SAT/SMT and constraint programming). A side-effect of the translation to Kodkod is that the ProB toolset now provides a double-chain (relying on technology developed independently and using different programming languages and paradigms) of validation for first-order predicates, which should prove relevant in high safety integrity level contexts.
In comparision with other formalisms Kodkod has the advantage that is provides good support for relations and sets which play an essential role in Event-B's mathematical notation.

LTL
ProB supports LTL model checking. One problem when using LTL to validate a model is that counter-examples returned by the model checker are often hard to understand. A counter-example typically consists of a lasso-chaped sequence of states and events. Instead of just loading the sequence into the history of the animator, we have implemented a dedicated visualisation for LTL counter-examples. The visualisation which is now part of ProB's Rodin plug-in shows why an LTL operator is true or false in each state of the sequence.

CSP and B
ProB supports also other formalisms like CSP. CSP can also be used to guide B and Event-B models and can also be used for specifying scenarios or for model testing. Within the project this feature of ProB was continuously maintained and improved. We have extended the implementation of the CSP interpreter and animator to be able to support more complex and larger data types (e.g. mixing of dot and non-associative tuples) as well as supporting more complicated pattern matching inside set comprehension formulas and function definitions. Some effort for supporting more of CSP built-in functions (like seq(-), set(-) and card(-))was made as well. Finally, ProB now supports checking LTL-assertions directly from the CSP model by using pragmas ({-# assert_ltl = … #-}). The syntax is the same as for LTL-assertions in DEFINITION clauses of B models.

Available Documentation

Constraint Solving
The improvements are available in the nightly builds of ProB.
Two specific pages have been added to the ProB user manual.

TLA2B
The TLA+ to B translation has been published at the iFM'2012 conference. A technical report is also available. A presentation at the FM'2012 TLA+ workshop will also be made, and a dedicated page has been added to the ProB user manual.

Physical Units
This work is still in progress. A first tutorial page is available in the ProB online documentation. Full documentation will be made available later in the project. The latest nightly build of ProB contains an experimental version of the analysis.

Kodkod
A technical report has been published on the validation using ProB and Kodkod. The paper has been accepted for FM'2012.

LTL
The concept and implemenation of the visualisation is described in the master thesis of Andriy Tolstoy.

BMotion Studio
A developer-, user documentation, tutorial and examples are available from a dedicated webpage hosted by the University of Duesseldorf.

Planning

Physical Units
Physical units work will be completed. First experiments with industrial models from Alstom are encouraging.

Kodkod
Currently the translation to Kodkod is only applied to axioms when trying to find values for the constants and during the constraint based deadlock check. We plan to restructure ProB's internal programming interfaces in a way that allows to apply Kodkod more easily and make it available for other checks (e.g. constraint-based invariant check, assertion checks).
We will evaluate how we can employ more SMT based techniques in ProB.

Constraint Solving
During the further development of ProB's constraint solving it became apparent that it would be helpful to represent the cardinality of a set by a CLP(FD) variable. We plan to change ProB's internal representation of sets in a way that its cardinality can be accessed in this way.
To allow a translation from ProB to Kodkod, we implemented an integer interval analysis. We plan to adapt the analysis to set up sizes of deferred sets. This is necessary because ProB chooses a fixed size for a deferred set and sometimes a model has only solutions for a certain size. Currently a user must supply a size manually.

LTL
Fairness properties are very common when specifying LTL formula. Fairness can be encoded by using standard LTL, but it makes the formula significantly larger. The complexity of the model checking algorithm grows exponentially with the number of used LTL operators in a formula. We plan to incorporate support for fairness directly into the model checker which should lead to a drastic improvement in performance when fairness is used. Additionally, the usability of the model checker is improved by having the ability to specify fairness conditions seperatly from the rest of the LTL formula.

BMotion Studio
We will provide a way to link up other Java-based simulation tools with BMotion Studio. Furthermore, beside working on identified bugs and and rectifying usability issues, we want to create more visual elements to aid humans understand large-scale simulations.