Billaude's work to finish
This page is here to describe the work that I started, but which is yet to be finished.
MembershipGoal
Here the rules that could be useful for the reasoner MembershipGoal.
| Inference Rule | Side condition | Implemented in the new version | Implemented in the first version |
|---|---|---|---|
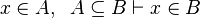
|

| ||
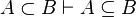
|

|

| |
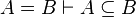
|

|

| |
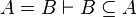
|

|

| |
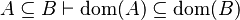
|

|

| |
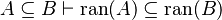
|

|

| |
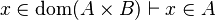
|

|

| |
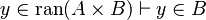
|

|

| |
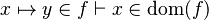
|

|

| |
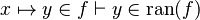
|

|

| |
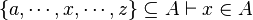
|

|

| |
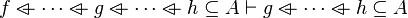
|

|

| |
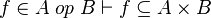
|
where 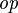 is one of is one of 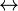 , , 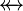 , , 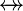 , , 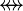 , , 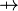 , , 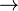 , , 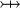 , , 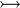 , , 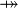 , , 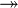 , , 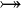
|

|

|
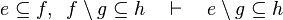
|

| ||
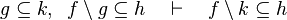
|

| ||
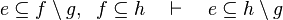
|

| ||
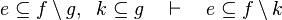
|

| ||
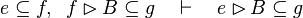
|

| ||
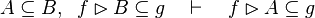
|

| ||
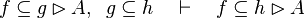
|

| ||
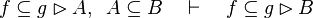
|

| ||
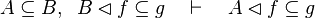
|

| ||
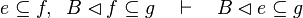
|

| ||
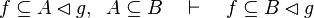
|

| ||
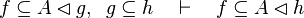
|

| ||
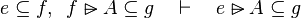
|

| ||
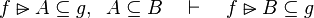
|

| ||
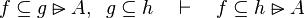
|

| ||
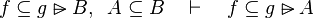
|

| ||
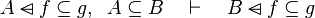
|

| ||
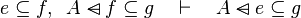
|

| ||
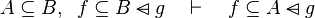
|

| ||
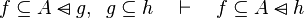
|

| ||
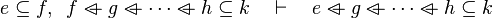
|

| ||
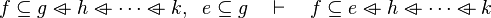
|

| ||
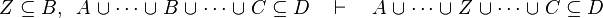
|

| ||
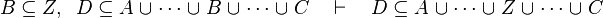
|

| ||
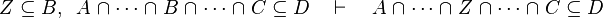
|

| ||
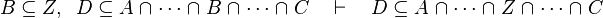
|

| ||
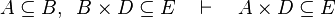
|

| ||
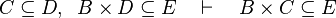
|

| ||
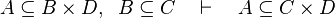
|

| ||
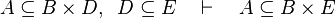
|

| ||
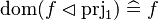
|

| ||
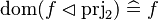
|

| ||
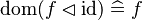
|

| ||
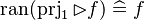
|

| ||
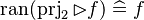
|

| ||
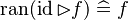
|

| ||
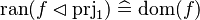
|

| ||
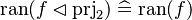
|

| ||
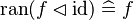
|

|
This describe the rule that I implemented in the first version of MembershipGoal. Others should also be taken into account (they will be written later). Even if those rule have been checked, they may not be implemented in the reasoner since some can explode the time research.
Membership Goal Exhaustive rules
To be completed ...
Autorewriter
In the AutorewriterL3, some re-writing about 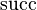 and
and 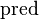 are proceeded. But, more re-writing should be done. Unfortunately, I did not take too much time to analyze all the possibilities about this two functions
are proceeded. But, more re-writing should be done. Unfortunately, I did not take too much time to analyze all the possibilities about this two functions 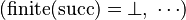 .
.
Nevertheless, one trail has been explored : instead of re-writing 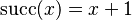 , we may should better re-write :
, we may should better re-write : 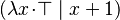 .
.
Moreover, since 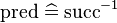 , instead of re-writing
, instead of re-writing 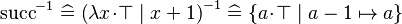 (the last re-writing is proceeded by the auto-rewriter, and is not really easy to read), I think that we should re-write
(the last re-writing is proceeded by the auto-rewriter, and is not really easy to read), I think that we should re-write 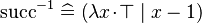 .
.
Others Feature Requests
The feature request #2887264 should also be treated.