D32 Mathematical Extensions
Overview
Mathematical extensions have been co-developed by Systerel (for the Core Rodin Platform) and Southampton (for the Theory plug-in). The main purpose of this new feature was to provide the Rodin user with a way to extend the standard Event-B mathematical language by supporting user-defined operators, basic predicates and algebraic types. Along with these additional notations, the user can also define new proof rules (prover extensions).
A theory is a file that can be used to define new algebraic types, new operators/predicates and new proof rules. Theories are developed in the Rodin workspace, and proof obligations are generated to validate prover and mathematical extensions. When a theory is completed and (optionally) validated, the user can make it available for use in models (this action is called the deployment of a theory). Theories are deployed to the current workspace (i.e., Workspace Scope), and the user can use any defined extensions in any project within the workspace.
Records Plug-in has been developed by University of Southampton before the mathematical extensions as a new feature to provide structured types in Event-B. The plug-in extends Rodin standard context editor with a new modelling construct to provide support for structured types, which can be defined in terms of two new clauses: record declarations and record extensions. Both enable users to define their custom reusable types, that are treated underline by Rodin as Event-B constant sets and relations, supported by additional axioms, which the plug-in generates to simplify the proofs.
Motivations
Main reasons for implementing mathematical extensions are:
- increased readability (
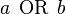rather than 
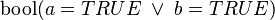) - polymorphism (
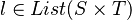) - decreased proving effort, thanks to extension specific proof rules instead of general purpose ones
The Theory plug-in superseded the Rule-based Prover v0.3 plug-in, and is the placeholder for mathematical and prover extensions. It provides a high-level interface to the Rodin Core capabilities with regards to mathematical extensions. The Rule-based Prover was originally devised to provide an usable mechanism for user-defined rewrite rules through theories. Theories were, then, deemed a natural choice for defining mathematical extensions as well as proof rules to reason about such extensions. In essence, the Theory plug-in provides a systematic platform for defining and validating extensions through a familiar technique: proof obligations.
The motivation for development of Records plug-in was to fill the gap in Event-B language - a missing support of a syntax for the direct definition of structured types. Some of the industrial partners expressed a desire to have this missing feature in Event-B, that would allow them to define their own structured types such as records or classes. Theoretically these structures could be modelled with existing Event-B capabilities via projection functions. Backed up by a refined theoretical proposal Records plug-in was developed to extend the standard Event-B notation with requested capability.
Choices / Decisions
On the Core Rodin Platform side, implementing mathematical extensions required to make some parts of the code extensible, that were not designed to be so, namely the lexer and the parser. We were using tools that automatically generated them from a fixed grammar description, so we had to change to other technologies. A study has been made on available technologies. The Pratt algorithm was selected for its adequation with the purpose and it did not have the drawbacks of other technologies:
- foreign language integration
- overhead due to over generality
After a mocking up phase to verify feasibility, the Pratt algorithm has been confirmed as the chosen option and implemented in the Rodin Platform.
Besides, we wanted to set up a way to publish and share theories for Rodin users, in order to constitute a database of pre-built theories for everyone to use and contribute. This has been realised by adding a new tracker on SourceForge site ([1]).
The Theory plug-in contributes a theory construct to the Rodin database. Theories were used in the Rule-based Prover (before it was discontinued) as a placeholder for rewrite rules. Given the usability advantages of the theory component, it was decided to use it to define mathematical extensions (new operators and new datatypes). Another advantage of using the theory construct is the possibility of using proof obligations to ensure that the soundness of the formalism is not compromised. Proof obligations are generated to validate any properties of new operators (e.g., associativity). With regards to prover extensions, it was decided that the Theory plug-in inherits the capabilities to define and validate rewrite rules from the Rule-based Prover. Furthermore, support for a simple yet powerful subset of inference rules is added, and polymorphic theorems can be defined within the same setting. Proof obligations are, again, used as a filter against potentially unsound proof rules.
Records plug-in required the extension of the Rodin database with the new constructs to support structured types. On the other hand the Event-B language itself did not support extension at that time. For that reason the decision was made to address extensibility problem at the lowest level possible, which was Rodin database, but to model structured types using standard Event-B notation at the level below. The translation from extended to standard syntax has been entrusted to the static checker, that was also extended for this purpose. Thus the plug-in provides the users with notation for record declarations and extensions in unchecked models, but the checked versions operate with standard Event-B constructs.
Available Documentation
- Pre-studies (states of the art, proposals, discussions).
- Technical details (specifications).
- Teaching materials (tutorials).
- User's guides.
Planning
The Theory plug-in v2.1 is released. Work will continue on general maintenance, bug fixes as well adding new features as requested by the users of the plug-in.
