Extension Proof Rules
From Event-B
Jump to navigationJump to search
Rules that are marked with a * in the first column are implemented in the latest version of Rodin. Rules without a * are planned to be implemented in future versions. Other conventions used in these tables are described in The_Proving_Perspective_(Rodin_User_Manual)#Rewrite_Rules.
Rewrite Rules
| Name | Rule | Side Condition | A/M | |
|---|---|---|---|---|
| * | SIMP_SPECIAL_COND_BTRUE |
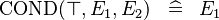 |
A | |
| * | SIMP_SPECIAL_COND_BFALSE |
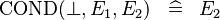 |
A | |
| * | SIMP_MULTI_COND |
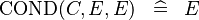 |
A |
Inference Rules
| Name | Rule | Side Condition | A/M | |
|---|---|---|---|---|
| * | DATATYPE_DISTINCT_CASE |
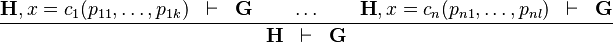 |
where  has a datatype has a datatype 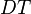 as type and appears free in as type and appears free in 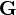 , , 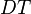 has constructors has constructors 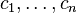 , parameters , parameters 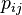 are introduced as fresh identifiers are introduced as fresh identifiers |
M
|
| * | DATATYPE_INDUCTION |
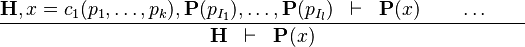 |
where  has inductive datatype has inductive datatype 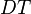 as type and appears free in as type and appears free in 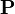 ; ; 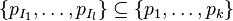 are the inductive parameters (if any); an antecedent is created for every constructor are the inductive parameters (if any); an antecedent is created for every constructor 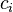 of of 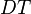 ; all parameters are introduced as fresh identifiers; examples here ; all parameters are introduced as fresh identifiers; examples here |
M |