Extension Proof Rules: Difference between revisions
From Event-B
Jump to navigationJump to search
imported>Nicolas m copied datatype inference rules |
imported>WikiSysop |
||
| (5 intermediate revisions by 3 users not shown) | |||
| Line 3: | Line 3: | ||
Other conventions used in these tables are described in [[The_Proving_Perspective_%28Rodin_User_Manual%29#Rewrite_Rules]]. | Other conventions used in these tables are described in [[The_Proving_Perspective_%28Rodin_User_Manual%29#Rewrite_Rules]]. | ||
== Rewrite Rules == | === Rewrite Rules === | ||
{{RRHeader}} | {{RRHeader}} | ||
{{RRRow}}|*||{{Rulename|SIMP_SPECIAL_COND_BTRUE}}||<math> \operatorname{COND}(\btrue, E_1, E_2) \;\;\defi\;\; E_1 </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_SPECIAL_COND_BTRUE}}||<math> \operatorname{COND}(\btrue, E_1, E_2) \;\;\defi\;\; E_1 </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_SPECIAL_COND_BFALSE}}||<math> \operatorname{COND}(\bfalse, E_1, E_2) \;\;\defi\;\; E_2 </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_SPECIAL_COND_BFALSE}}||<math> \operatorname{COND}(\bfalse, E_1, E_2) \;\;\defi\;\; E_2 </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_MULTI_COND}}||<math> \operatorname{COND}(C, E, E) \;\;\defi\;\; E </math>|| || A | |||
|} | |} | ||
=== Inference Rules === | |||
== Inference Rules == | |||
{{RRHeader}} | {{RRHeader}} | ||
{{RRRow}}| ||{{Rulename|DATATYPE_DISTINCT_CASE}}||<math>\frac{\textbf{H}, x=c_1(p_{11}, \ldots, p_{1k}) \;\;\vdash \;\; \textbf{G} \qquad \ldots \qquad \textbf{H}, x=c_n(p_{n1}, \ldots, p_{nl}) \;\;\vdash \;\; \textbf{G} }{ \textbf{H} \;\;\vdash\;\; \textbf{G} }</math>|| where <math>x</math> has a datatype <math>DT</math> as type and appears free in <math>\textbf{G}</math>, <math>DT</math> has constructors <math>c_1, \ldots, c_n</math>, parameters <math>p_{ij}</math> are introduced as fresh identifiers || M | {{RRRow}}|*||{{Rulename|DATATYPE_DISTINCT_CASE}}||<math>\frac{\textbf{H}, x=c_1(p_{11}, \ldots, p_{1k}) \;\;\vdash \;\; \textbf{G} \qquad \ldots \qquad \textbf{H}, x=c_n(p_{n1}, \ldots, p_{nl}) \;\;\vdash \;\; \textbf{G} }{ \textbf{H} \;\;\vdash\;\; \textbf{G} }</math>|| where <math>x</math> has a datatype <math>DT</math> as type and appears free in <math>\textbf{G}</math>, <math>DT</math> has constructors <math>c_1, \ldots, c_n</math>, parameters <math>p_{ij}</math> are introduced as fresh identifiers || M | ||
{{RRRow}}| ||{{Rulename|DATATYPE_INDUCTION}}||<math>\frac{ \textbf{H}, x=c_1(p_1, \ldots, p_k),\textbf{P}(p_{I_1}), \ldots, \textbf{P}(p_{I_l}) \;\;\vdash \;\; \textbf{P}(x) \qquad \ldots \qquad}{ \textbf{H} \;\;\vdash\;\; \textbf{P}(x) }</math>|| where <math>x</math> has inductive datatype <math>DT</math> as type and appears free in <math>\textbf{P}</math>; <math>\{p_{I_1}, \ldots, p_{I_l}\} \subseteq \{p_1, \ldots, p_k\}</math> are the inductive parameters (if any); an antecedent is created for every constructor <math>c_i</math> of <math>DT</math>; all parameters are introduced as fresh identifiers; examples [[Datatype Rules|here]] || M | {{RRRow}}|*||{{Rulename|DATATYPE_INDUCTION}}||<math>\frac{ \textbf{H}, x=c_1(p_1, \ldots, p_k),\textbf{P}(p_{I_1}), \ldots, \textbf{P}(p_{I_l}) \;\;\vdash \;\; \textbf{P}(x) \qquad \ldots \qquad}{ \textbf{H} \;\;\vdash\;\; \textbf{P}(x) }</math>|| where <math>x</math> has inductive datatype <math>DT</math> as type and appears free in <math>\textbf{P}</math>; <math>\{p_{I_1}, \ldots, p_{I_l}\} \subseteq \{p_1, \ldots, p_k\}</math> are the inductive parameters (if any); an antecedent is created for every constructor <math>c_i</math> of <math>DT</math>; all parameters are introduced as fresh identifiers; examples [[Datatype Rules|here]] || M | ||
|} | |} | ||
Latest revision as of 15:38, 29 November 2019
Rules that are marked with a * in the first column are implemented in the latest version of Rodin. Rules without a * are planned to be implemented in future versions. Other conventions used in these tables are described in The_Proving_Perspective_(Rodin_User_Manual)#Rewrite_Rules.
Rewrite Rules
| Name | Rule | Side Condition | A/M | |
|---|---|---|---|---|
| * | SIMP_SPECIAL_COND_BTRUE |
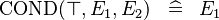 |
A | |
| * | SIMP_SPECIAL_COND_BFALSE |
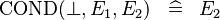 |
A | |
| * | SIMP_MULTI_COND |
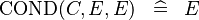 |
A |
Inference Rules
| Name | Rule | Side Condition | A/M | |
|---|---|---|---|---|
| * | DATATYPE_DISTINCT_CASE |
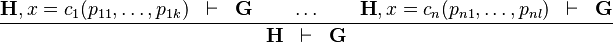 |
where  has a datatype has a datatype 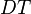 as type and appears free in as type and appears free in 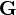 , , 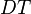 has constructors has constructors 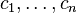 , parameters , parameters 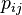 are introduced as fresh identifiers are introduced as fresh identifiers |
M
|
| * | DATATYPE_INDUCTION |
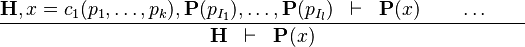 |
where  has inductive datatype has inductive datatype 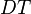 as type and appears free in as type and appears free in 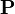 ; ; 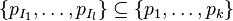 are the inductive parameters (if any); an antecedent is created for every constructor are the inductive parameters (if any); an antecedent is created for every constructor 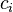 of of 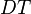 ; all parameters are introduced as fresh identifiers; examples here ; all parameters are introduced as fresh identifiers; examples here |
M |