State-Machines and Code Generation: Difference between revisions

From Event-B
Jump to navigationJump to search
← Older edit
imported>Andy
imported>Andy
 
(9 intermediate revisions by the same user not shown)
Line 22: Line 22:
</div>
</div>


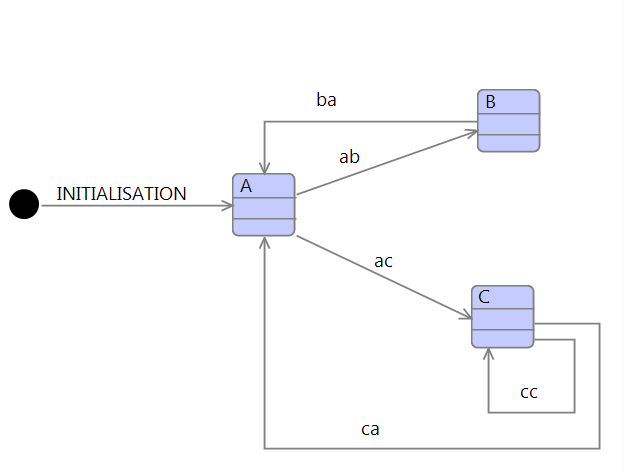
We generate a subroutine that controls the state machine, and code, in the task body, to call the subroutines once in every execution cycle. Each state in the state machine is related to a case statement in the subroutine. For instance, the Ada code for the diagram in Figure 1 is,
We generate a subroutine that controls the state machine, and implements the actions. In the task body, we add a call the state-machine subroutines once in every execution cycle. Each state in the state machine is related to a case statement in the subroutine. For instance, the Ada code for the diagram in Figure 1 is,


  case sm_state is
  case sm_state is
  when A => <body> ; sm_state := B;
  when A => <''body''> ; sm_state := B;
  when B => <body> ; sm_state := A;
  when B => <''body''> ; sm_state := A;
  ...  
  ...  


The <body> translation is determined, in part, by the number of outgoing transitions and the guards and actions of the elaborated events. When a state has a single outgoing transition, then the translation is straightforward. The event's action is mapped to a statement in the generated IL1 model. When a state has multiple outgoing transitions, then each outgoing transition of the state gives rise to a branching statement. Each outgoing transition is linked to an event, and the guards of the outgoing transitions must be disjoint and complete. Note that we do not yet generate proof obligations to show this. We illustrate the translation with an example, below. If we define the events, elaborating the transitions in the diagram, as follows: with a machine  variable v:INT and events ''ab'' and ''ac'' defined below,
The <''body''> translation is determined, in part, by the number of outgoing transitions and the guards and actions of the elaborated events. When a state has a single outgoing transition, then the translation is straightforward. The event's action is mapped to a statement in the generated IL1 model. When a state has multiple outgoing transitions, then each outgoing transition of the state gives rise to a branching statement. Each outgoing transition is linked to an event, and the guards of the outgoing transitions must be disjoint and complete. Note that we do not yet generate proof obligations to show this. We illustrate the translation with an example fragment of the machine of Figure 1; the fragment refers to a variable ''vv: INT'', and events ''ab'' and ''ac'', which elaborate the transitions in the diagram.
ab = when vv < 100 then <''a1''> end
ac = when vv >= 100 then <''a2''> end


ab = when v < 100 then <a1> end;
The body can be viewed as a parallel composition of events, made up of all of the outgoing transitions of ''State A''. These events have disjoint and complete guards, so only one of the events will be enabled. The translation of the body gives rise to the following branching statement when translated to Ada,  
ac = when v >= 100 then <a2> end
 
  if vv < 100 then <''a1''>
Then this is translated to a branching statement, as in this example translation to Ada:  
  elsif vv >= 100 then <''a2''>
 
  if v < 100 then <a1>
  elsif v >= 100 then <a2>
  end if;
  end if;


== Tooling ==
See all of the Ada code that is generated [http://wiki.event-b.org/images/Code.png here].

Latest revision as of 09:47, 17 May 2012

Generating Code from State-Machine Diagrams

We have introduced the ability to generate code from state-machine diagrams, in version 0.2.3 of the code generation feature plug-in. Implementation code is generated from the diagram itself, and no additional mark-up of the model is required; that is, nothing over and above the usual mark-up required for Tasking Event-B, such as identifying non-typing/typing invariants, and guards etc. State-machines are created, using the existing state-machine plug-in, subject to the limitations described below.

Limitations

The current code generation tool is restricted to generating code for a single Event-B machine, which may contain one or more state-machines. We have yet to explore the decomposition/composition of machines containing state-machines. In principal we should be able to apply decomposition techniques to decompose the single Event-B machine with state-machines into a number of machines, with the state-machines, or the elements of state-machines, distributed between them.

Another limitation is that we do not handle nested state-machines, although this should be feasible.

Only the state-machines of tasking/environ machines generate code. State-machines of shared machines do not generate code. This should be explored further during research into decomposition.

Translations

The translation of the diagrammatic elements to code has been hard-coded in the code generation plug-in. We have introduced new types to the translator's common language model (IL1). We add case-statements, and a container for them (analogous to switch) since these are commonly used to implement state-machines. The code generator navigates through each state of a state-machine, generating an internal representation of the state-machine, which is used to create the IL1 model. The IL1 model is then used to generate code for the various target languages that may have been implemented. We have also updated the IL1-to-target code generators, to generate case/switch statements in Ada, C and Java.

Each state-machine has an Enumerated type whose elements take the names of the states. A state variable is created in the target that keeps track of the current state, and has the type of the enumeration.

An Example


caption text
caption text
Figure 1: Example State-machine Diagram


We generate a subroutine that controls the state machine, and implements the actions. In the task body, we add a call the state-machine subroutines once in every execution cycle. Each state in the state machine is related to a case statement in the subroutine. For instance, the Ada code for the diagram in Figure 1 is, 

case sm_state is
when A => <body> ; sm_state := B;
when B => <body> ; sm_state := A;
...

The <body> translation is determined, in part, by the number of outgoing transitions and the guards and actions of the elaborated events. When a state has a single outgoing transition, then the translation is straightforward. The event's action is mapped to a statement in the generated IL1 model. When a state has multiple outgoing transitions, then each outgoing transition of the state gives rise to a branching statement. Each outgoing transition is linked to an event, and the guards of the outgoing transitions must be disjoint and complete. Note that we do not yet generate proof obligations to show this. We illustrate the translation with an example fragment of the machine of Figure 1; the fragment refers to a variable vv: INT, and events ab and ac, which elaborate the transitions in the diagram. 

ab = when vv < 100 then <a1> end 
ac = when vv >= 100 then <a2> end

The body can be viewed as a parallel composition of events, made up of all of the outgoing transitions of State A. These events have disjoint and complete guards, so only one of the events will be enabled. The translation of the body gives rise to the following branching statement when translated to Ada, 

if vv < 100 then <a1>
elsif vv >= 100 then <a2>
end if;

See all of the Ada code that is generated here.

Retrieved from ‘https://wiki.event-b.org/index.php?title=State-Machines_and_Code_Generation&oldid=9505’