Mathematical Extensions

Currently the operators and basic predicates of the Event-B mathematical language supported by Rodin are fixed. We propose to extend Rodin to define basic predicates, new operators or new algebraic types.

Requirements

User Requirements

• Binary operators (prefix form, infix form or suffix form).
• Operators on boolean expressions.
• Unary operators, such as absolute values.

Note that the pipe, which is already used for set comprehension, cannot be used to enter absolute values (in fact, as in the new design the pipe used in set comprehension is only a syntaxic sugar, the same symbol may be used for absolute value. To be confirmed with the prototyped parser"" -Mathieu ).

• Basic predicates (e.g., the symmetry of relations $sym(R) \defi R=R^{-1}$).

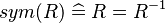Having a way to enter such predicates may be considered as syntactic sugar, because it is already possible to use sets (e.g., 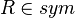$R \in sym$, where 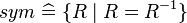$sym \defi \{R \mid R=R ^{-1}\}$) or functions (e.g., 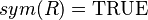$sym(R) = \True$, where $sym \defi (\lambda R \qdot R \in A \rel B \mid \bool(R = R^{-1}))$).

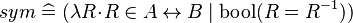• Quantified expressions (e.g., $\sum x \qdot P \mid y$, $\prod x \qdot P \mid y$, $~\min(S)$, $~\max(S)$).
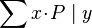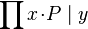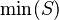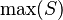• Types.
  • Enumerated types.
  • Scalar types.

User Input

The end-user shall provide the following information:

• Lexicon and Syntax.
  More precisely, it includes the symbols, the form (prefix, infix, postfix), the grammar, associativity (left-associative or right associative), commutativity, priority, the mode (flattened or not), ...
• Pretty-print.
  Alternatively, the rendering may be determined from the notation parameters passed to the parser.
• Typing rules.
• Well-definedness.

Development Requirements

• Scalability.

Towards a generic AST

The following AST parts are to become generic, or at least parameterised:

• Lexer
• Parser
• Nodes ( Formula class hierarchy ): parameters needed for:
  • Type Solve (type rule needed to synthesize the type)
  • Type Check (type rule needed to verify constraints on children types)
  • WD (WD predicate)
  • PrettyPrint (tag image + notation (prefix, infix, postfix))
  • Visit Formula (getting children + visitor callback mechanism)
  • Rewrite Formula (associative formulæ have a specific flattening treatment)
• Types (Type class hierarchy): parameters needed for:
  • Building the type expression (type rule needed)
  • PrettyPrint (set operator image)
  • getting Base / Source / Target type (type rule needed)
• Formula Factory
• Verification of preconditions (see for example AssociativeExpression.checkPreconditions)

Impact on other tools

Impacted plug-ins (use a factory to build formulæ):

• org.eventb.core

In particular, the static checker and proof obligation generator are impacted.

• org.eventb.core.seqprover
• org.eventb.pp
• org.eventb.pptrans
• org.eventb.ui

Open Questions

New types

Which option should we prefer for new types?

• OPTION #1: Transparent mode.

In transparent mode, it is always referred to the base type. As a consequence, the type conversion is implicitly supported (weak typing).

For example, it is possible to define the DISTANCE and SPEED types, which are both derived from the 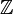$\intg$ base type, and to multiply a value of the former type with a value of the latter type.

• OPTION #2: Opaque mode.

In opaque mode, it is never referred to the base type. As a consequence, values of one type cannot be converted to another type (strong typing).

Thus, the above multiplication is not allowed.

This approach has at least two advantages:

- Stronger type checking.

- Better prover performances.

• OPTION #3: Mixed mode.

In mixed mode, the transparent mode is applied to scalar types and the opaque mode is applied to other types.

Scope of the mathematical extensions

• OPTION #1: Project scope.

The mathematical extensions are implicitly visible to all components of the project that has imported them.

• OPTION #2: Component scope.

The mathematical extensions are only visible to the components that have explicitly imported them.

Bibliography

• J.R. Abrial, M.Butler, M.Schmalz, S.Hallerstede, L.Voisin, Proposals for Mathematical Extensions for Event-B, 2009.

This proposal consists in considering three kinds of extension:

1. Extensions of set-theoretic expressions or predicates: example extensions of this kind consist in adding the transitive closure of relations or various ordered relations.
2. Extensions of the library of theorems for predicates and operators.
3. Extensions of the Set Theory itself through the definition of algebraic types such as lists or ordered trees using new set constructors.