Empty Set Rewrite Rules: Difference between revisions
From Event-B
Jump to navigationJump to search
imported>Laurent Update introduction about variants of the rules |
imported>Josselin Added rules EQUAL_TYPE (Type set) |
||
| Line 9: | Line 9: | ||
{{RRRow}}|||{{Rulename|SIMP_SETENUM_EQUAL_EMPTY}}||<math> \{ A, \ldots , B\} = \emptyset \;\;\defi\;\; \bfalse </math>|| || A | {{RRRow}}|||{{Rulename|SIMP_SETENUM_EQUAL_EMPTY}}||<math> \{ A, \ldots , B\} = \emptyset \;\;\defi\;\; \bfalse </math>|| || A | ||
{{RRRow}}|*||{{Rulename|SIMP_SPECIAL_EQUAL_COMPSET}}||<math> \{ x \qdot P(x) \mid E \} = \emptyset \;\;\defi\;\; \forall x\qdot \lnot\, P(x) </math>|| || A | {{RRRow}}|*||{{Rulename|SIMP_SPECIAL_EQUAL_COMPSET}}||<math> \{ x \qdot P(x) \mid E \} = \emptyset \;\;\defi\;\; \forall x\qdot \lnot\, P(x) </math>|| || A | ||
{{RRRow}}|||{{Rulename|SIMP_BINTER_EQUAL_TYPE}}||<math> A \binter \ldots \binter B = \mathit{Ty} \;\;\defi\;\; A = \mathit{Ty} \land \ldots \land B = \mathit{Ty} </math>|| where <math>\mathit{Ty}</math> is a type expression || A | |||
{{RRRow}}|||{{Rulename|SIMP_BUNION_EQUAL_EMPTY}}||<math> A \bunion \ldots \bunion B = \emptyset \;\;\defi\;\; A = \emptyset \land \ldots \land B = \emptyset </math>|| || A | {{RRRow}}|||{{Rulename|SIMP_BUNION_EQUAL_EMPTY}}||<math> A \bunion \ldots \bunion B = \emptyset \;\;\defi\;\; A = \emptyset \land \ldots \land B = \emptyset </math>|| || A | ||
{{RRRow}}|||{{Rulename|SIMP_SETMINUS_EQUAL_EMPTY}}||<math> A \setminus B = \emptyset \;\;\defi\;\; A \subseteq B </math>|| || A | {{RRRow}}|||{{Rulename|SIMP_SETMINUS_EQUAL_EMPTY}}||<math> A \setminus B = \emptyset \;\;\defi\;\; A \subseteq B </math>|| || A | ||
{{RRRow}}|||{{Rulename|SIMP_SETMINUS_EQUAL_TYPE}}||<math> A \setminus B = \mathit{Ty} \;\;\defi\;\; A = \mathit{Ty} \land B = \emptyset </math>|| where <math>\mathit{Ty}</math> is a type expression || A | |||
{{RRRow}}|||{{Rulename|SIMP_POW_EQUAL_EMPTY}}||<math> \pow (S) = \emptyset \;\;\defi\;\; \bfalse </math>|| || A | {{RRRow}}|||{{Rulename|SIMP_POW_EQUAL_EMPTY}}||<math> \pow (S) = \emptyset \;\;\defi\;\; \bfalse </math>|| || A | ||
{{RRRow}}|||{{Rulename|SIMP_POW1_EQUAL_EMPTY}}||<math> \pown (S) = \emptyset \;\;\defi\;\; S = \emptyset </math>|| || A | {{RRRow}}|||{{Rulename|SIMP_POW1_EQUAL_EMPTY}}||<math> \pown (S) = \emptyset \;\;\defi\;\; S = \emptyset </math>|| || A | ||
{{RRRow}}|||{{Rulename|SIMP_KUNION_EQUAL_EMPTY}}||<math> \union (S) = \emptyset \;\;\defi\;\; S \subseteq \{ \emptyset \} </math>|| || A | {{RRRow}}|||{{Rulename|SIMP_KINTER_EQUAL_TYPE}}||<math> \inter (S) = \mathit{Ty} \;\;\defi\;\; S = \{ \mathit{Ty} \} </math>|| where <math>\mathit{Ty}</math> is a type expression || A | ||
{{RRRow}}|||{{Rulename|SIMP_KUNION_EQUAL_EMPTY}}||<math> \union (S) = \emptyset \;\;\defi\;\; S \subseteq \{ \emptyset \} </math>|| || A | |||
{{RRRow}}|||{{Rulename|SIMP_QINTER_EQUAL_TYPE}}||<math> (\Inter x\qdot P(x) \mid E(x)) = \mathit{Ty} \;\;\defi\;\; \forall x\qdot P(x) \limp E(x) = \mathit{Ty}</math>|| where <math>\mathit{Ty}</math> is a type expression || A | |||
{{RRRow}}|||{{Rulename|SIMP_QUNION_EQUAL_EMPTY}}||<math> (\Union x\qdot P(x) \mid E(x)) = \emptyset \;\;\defi\;\; \forall x\qdot P(x) \limp E(x) = \emptyset</math>|| || A | {{RRRow}}|||{{Rulename|SIMP_QUNION_EQUAL_EMPTY}}||<math> (\Union x\qdot P(x) \mid E(x)) = \emptyset \;\;\defi\;\; \forall x\qdot P(x) \limp E(x) = \emptyset</math>|| || A | ||
{{RRRow}}|||{{Rulename|SIMP_NATURAL_EQUAL_EMPTY}}||<math> \nat = \emptyset \;\;\defi\;\; \bfalse</math>|| || A | {{RRRow}}|||{{Rulename|SIMP_NATURAL_EQUAL_EMPTY}}||<math> \nat = \emptyset \;\;\defi\;\; \bfalse</math>|| || A | ||
| Line 19: | Line 23: | ||
{{RRRow}}|*||{{Rulename|SIMP_TYPE_EQUAL_EMPTY}}||<math> \mathit{Ty} = \emptyset \;\;\defi\;\; \bfalse </math>|| where <math>\mathit{Ty}</math> is a type expression || A | {{RRRow}}|*||{{Rulename|SIMP_TYPE_EQUAL_EMPTY}}||<math> \mathit{Ty} = \emptyset \;\;\defi\;\; \bfalse </math>|| where <math>\mathit{Ty}</math> is a type expression || A | ||
{{RRRow}}|||{{Rulename|SIMP_CPROD_EQUAL_EMPTY}}||<math> S \cprod T = \emptyset \;\;\defi\;\; S = \emptyset \lor T = \emptyset </math>|| || A | {{RRRow}}|||{{Rulename|SIMP_CPROD_EQUAL_EMPTY}}||<math> S \cprod T = \emptyset \;\;\defi\;\; S = \emptyset \lor T = \emptyset </math>|| || A | ||
{{RRRow}}|||{{Rulename|SIMP_CPROD_EQUAL_TYPE}}||<math> S \cprod T = \mathit{Ty} \;\;\defi\;\; S = \mathit{Ta} \land T = \mathit{Tb} </math>|| where <math>\mathit{Ty}</math> is a type expression equal to <math>\mathit{Ta} \cprod \mathit{Tb}</math> || A | |||
{{RRRow}}|||{{Rulename|SIMP_UPTO_EQUAL_EMPTY}}||<math> i \upto j = \emptyset \;\;\defi\;\; i > j </math>|| || A | {{RRRow}}|||{{Rulename|SIMP_UPTO_EQUAL_EMPTY}}||<math> i \upto j = \emptyset \;\;\defi\;\; i > j </math>|| || A | ||
{{RRRow}}|||{{Rulename|SIMP_UPTO_EQUAL_INT}}||<math> i \upto j = \intg \;\;\defi\;\; \bfalse </math>|| || A | |||
{{RRRow}}|*||{{Rulename|SIMP_SPECIAL_EQUAL_REL}}||<math> A \rel B = \emptyset \;\;\defi\;\; \bfalse </math>|| idem for operators <math>\pfun \pinj</math> || A | {{RRRow}}|*||{{Rulename|SIMP_SPECIAL_EQUAL_REL}}||<math> A \rel B = \emptyset \;\;\defi\;\; \bfalse </math>|| idem for operators <math>\pfun \pinj</math> || A | ||
{{RRRow}}|*||{{Rulename|SIMP_SPECIAL_EQUAL_RELDOM}}||<math> A \trel B = \emptyset \;\;\defi\;\; \lnot\, A = \emptyset \land B = \emptyset </math>|| idem for operator <math>\tfun</math> || A | {{RRRow}}|*||{{Rulename|SIMP_SPECIAL_EQUAL_RELDOM}}||<math> A \trel B = \emptyset \;\;\defi\;\; \lnot\, A = \emptyset \land B = \emptyset </math>|| idem for operator <math>\tfun</math> || A | ||
Revision as of 10:12, 21 May 2013
Rules that are marked with a * in the first column are implemented in the latest version of Rodin. Rules without a * are planned to be implemented in future versions. Other conventions used in these tables are described in The_Proving_Perspective_(Rodin_User_Manual)#Rewrite_Rules.
All rewrite rules that match the pattern 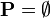 are also applicable to predicates of the form
are also applicable to predicates of the form 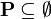 and
and 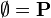 , as these predicates are equivalent.
, as these predicates are equivalent.
| Name | Rule | Side Condition | A/M | |
|---|---|---|---|---|
| * | DEF_SPECIAL_NOT_EQUAL |
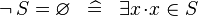 |
where  is not free in is not free in  |
M |
SIMP_SETENUM_EQUAL_EMPTY |
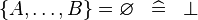 |
A | ||
| * | SIMP_SPECIAL_EQUAL_COMPSET |
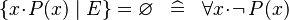 |
A | |
SIMP_BINTER_EQUAL_TYPE |
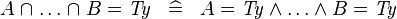 |
where  is a type expression is a type expression |
A | |
SIMP_BUNION_EQUAL_EMPTY |
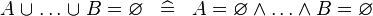 |
A | ||
SIMP_SETMINUS_EQUAL_EMPTY |
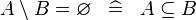 |
A | ||
SIMP_SETMINUS_EQUAL_TYPE |
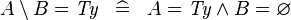 |
where  is a type expression is a type expression |
A | |
SIMP_POW_EQUAL_EMPTY |
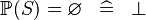 |
A | ||
SIMP_POW1_EQUAL_EMPTY |
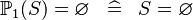 |
A | ||
SIMP_KINTER_EQUAL_TYPE |
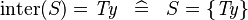 |
where  is a type expression is a type expression |
A | |
SIMP_KUNION_EQUAL_EMPTY |
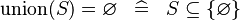 |
A | ||
SIMP_QINTER_EQUAL_TYPE |
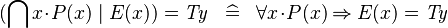 |
where  is a type expression is a type expression |
A | |
SIMP_QUNION_EQUAL_EMPTY |
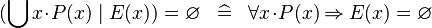 |
A | ||
SIMP_NATURAL_EQUAL_EMPTY |
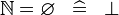 |
A | ||
SIMP_NATURAL1_EQUAL_EMPTY |
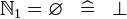 |
A | ||
| * | SIMP_TYPE_EQUAL_EMPTY |
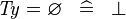 |
where  is a type expression is a type expression |
A |
SIMP_CPROD_EQUAL_EMPTY |
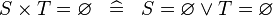 |
A | ||
SIMP_CPROD_EQUAL_TYPE |
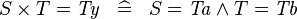 |
where  is a type expression equal to is a type expression equal to 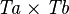 |
A | |
SIMP_UPTO_EQUAL_EMPTY |
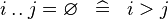 |
A | ||
SIMP_UPTO_EQUAL_INT |
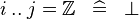 |
A | ||
| * | SIMP_SPECIAL_EQUAL_REL |
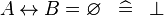 |
idem for operators 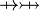 |
A |
| * | SIMP_SPECIAL_EQUAL_RELDOM |
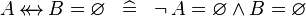 |
idem for operator 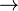 |
A |
SIMP_SREL_EQUAL_EMPTY |
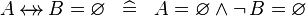 |
A | ||
SIMP_STREL_EQUAL_EMPTY |
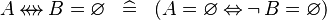 |
A | ||
SIMP_DOM_EQUAL_EMPTY |
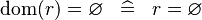 |
A | ||
SIMP_RAN_EQUAL_EMPTY |
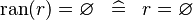 |
A | ||
SIMP_FCOMP_EQUAL_EMPTY |
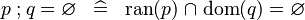 |
A | ||
SIMP_BCOMP_EQUAL_EMPTY |
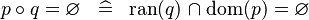 |
A | ||
SIMP_DOMRES_EQUAL_EMPTY |
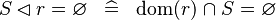 |
A | ||
SIMP_DOMSUB_EQUAL_EMPTY |
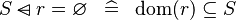 |
A | ||
SIMP_RANRES_EQUAL_EMPTY |
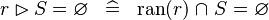 |
A | ||
SIMP_RANSUB_EQUAL_EMPTY |
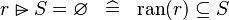 |
A | ||
SIMP_CONVERSE_EQUAL_EMPTY |
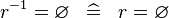 |
A | ||
SIMP_RELIMAGE_EQUAL_EMPTY |
![r[S] = \emptyset \;\;\defi\;\; S \domres r = \emptyset](/images/math/3/8/f/38f444db2941b8e696a89faeec9b7623.png) |
A | ||
SIMP_OVERL_EQUAL_EMPTY |
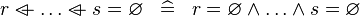 |
A | ||
SIMP_DPROD_EQUAL_EMPTY |
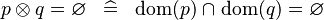 |
A | ||
SIMP_PPROD_EQUAL_EMPTY |
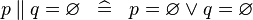 |
A | ||
SIMP_ID_EQUAL_EMPTY |
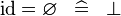 |
A | ||
SIMP_PRJ1_EQUAL_EMPTY |
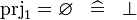 |
A | ||
SIMP_PRJ2_EQUAL_EMPTY |
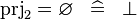 |
A |