Mathematical Extensions
From Event-B
Currently the operators and basic predicates of the Event-B mathematical language supported by Rodin are fixed. We propose to extend Rodin to define basic predicates, new operators or new algebraic types.
Requirements
Usage Requirements
- Binary operators (prefix form, infix form or suffix form).
- Operators on boolean expressions.
- Unary operators, such as absolute values.
- Note the the pipe, which is already used for set comprehension, cannot be used to enter absolute values.
- Basic predicates (e.g., the symmetry of relations
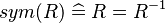 ).
).
- Having a way to enter such predicates may be considered as syntactic sugar, because it is already possible to use sets (e.g.,
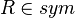 , where
, where 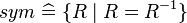 ) or functions (e.g.,
) or functions (e.g., 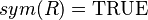 , where
, where 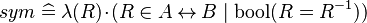 ).
).
- Quantified expressions (e.g.,
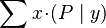 ,
, 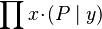 ,
, 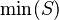 ,
, 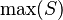 ).
).
Development Requirements
- Scalable developments.
Towards a generic AST
The following AST parts are to become generic, or at least parameterised:
- Lexer
- Parser
- Nodes ( Formula class hierarchy ): parameters needed for:
- Type Solve (type rule needed to synthesize the type)
- Type Check (type rule needed to verify constraints on children types)
- WD (WD predicate)
- PrettyPrint (tag image + notation (prefix, infix, postfix))
- Visit Formula (getting children + visitor callback mechanism)
- Rewrite Formula (associative formulæ have a specific flattening treatment)
- Types (Type class hierarchy): parameters needed for:
- Building the type expression (type rule needed)
- PrettyPrint (set operator image)
- getting Base / Source / Target type (type rule needed)
- Formula Factory
Impact on other tools
Impacted plug-ins (use a factory to build formulæ):
- org.eventb.core
- org.eventb.core.seqprover
- org.eventb.pp
- org.eventb.pptrans
- org.eventb.ui
Identified problems
Bibliography
- J.R. Abrial, M.Butler, M.Schmalz, S.Hallerstede, L.Voisin, Proposals for Mathematical Extensions for Event-B, 2009.
- This proposal consists in considering three kinds of extension:
- Extensions of set-theoretic expressions or predicates: example extensions of this kind consist in adding the transitive closure of relations or various ordered relations.
- Extensions of the library of theorems for predicates and operators.
- Extensions of the Set Theory itself through the definition of algebraic types such as lists or ordered trees using new set constructors.