Mathematical Extensions

Currently the operators and basic predicates of the Event-B mathematical language supported by Rodin are fixed. We propose to extend Rodin to define basic predicates, new operators or new algebraic types.

Requirements

User Requirements

• Binary operators (prefix form, infix form or suffix form).
• Operators on boolean expressions.
• Unary operators, such as absolute values.

Note that the pipe, which is already used for set comprehension, cannot be used to enter absolute values (in fact, as in the new design the pipe used in set comprehension is only a syntaxic sugar, the same symbol may be used for absolute value. To be confirmed with the prototyped parser. It may however be not allowed in a first time until backtracking is implemented, due to use of lookahead making assumptions on how the pipe symbol is used. -Mathieu ).

• Basic predicates (e.g., the symmetry of relations $sym(R) \defi R=R^{-1}$).

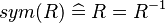Having a way to enter such predicates may be considered as syntactic sugar, because it is already possible to use sets (e.g., 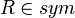$R \in sym$, where $sym \defi \{R \mid R=R ^{-1}\}$) or functions (e.g., $sym(R) = \True$, where $sym \defi (\lambda R \qdot R \in A \rel B \mid \bool(R = R^{-1}))$).

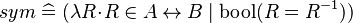• Quantified expressions (e.g., $\sum x \qdot P \mid y$, $\prod x \qdot P \mid y$, $~\min(S)$, $~\max(S)$).
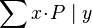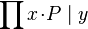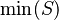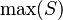• Types.
  • Enumerated types.
  • Scalar types.

User Input

The end-user shall provide the following information:

• keyboard input
• Lexicon and Syntax.
  More precisely, it includes the symbols, the form (prefix, infix, postfix), the grammar, associativity (left-associative or right associative), commutativity, priority, the mode (flattened or not), ...
• Pretty-print.
  Alternatively, the rendering may be determined from the notation parameters passed to the parser.
• Typing rules.
• Well-definedness.

Development Requirements

• Scalability.

Towards a generic AST

The following AST parts are to become generic, or at least parameterised:

• Lexer
• Parser
• Nodes ( Formula class hierarchy ): parameters needed for:
  • Type Solve (type rule needed to synthesize the type)
  • Type Check (type rule needed to verify constraints on children types)
  • WD (WD predicate)
  • PrettyPrint (tag image + notation (prefix, infix, postfix) + needs parentheses)
  • Visit Formula (getting children + visitor callback mechanism)
  • Rewrite Formula (associative formulæ have a specific flattening treatment)
• Types (Type class hierarchy): parameters needed for:
  • Building the type expression (type rule needed)
  • PrettyPrint (set operator image)
  • getting Base / Source / Target type (type rule needed)
• Verification of preconditions (see for example AssociativeExpression.checkPreconditions)

Vocabulary

An extension is to be understood as a single additional operator definition.

Tags

Every extension is associated with an integer tag, just like existing operators. Thus, questions arise about how to allocate new tags and how to deal with existing tags.
The solution proposed here consists in keeping existing tags 'as is'. They are already defined and hard coded in the Formula class, so this choice is made with backward compatibility in mind.

Now concerning extension tags, we will first introduce a few hypotheses:

• Tags_Hyp1: tags are never persisted across sessions on a given platform
• Tags_Hyp2: tags are never referenced for sharing purposes across various platforms

In other words, cross-platform/session formula references are always made through their String representation. These assumptions, which were already made and verified for Rodin before extensions, lead us to restrict further considerations to the scope of a single session on a single platform.

The following definitions hold at a given instant $t$ and for the whole platform.
Let 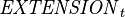$\mathit{EXTENSION}_t$ be the set of extensions supported by the platform at instant $t$;
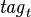let $\mathit{tag}_t$ denote the affectation of tags to a extensions at instant $t$ ($\mathit{tag}_t \in \mathit{EXTENSION}_t \pfun \intg$);
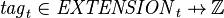let 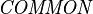$\mathit{COMMON}$ be the set of existing tags defined by the Formula class ($\mathit{COMMON} \sub \intg$).
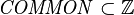The following requirements emerge:

• Tags_Req1: $\forall t \qdot \mathit{tag}_t \in \mathit{EXTENSION}_t \tinj \intg$
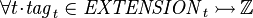
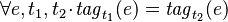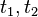• Tags_Req2: $\forall e, t_1,t_2 \qdot \mathit{tag}_{t_1}(e)=\mathit{tag}_{t_2}(e)$ where $t_1, t_2$ are two instants during a given session
• Tags_Req3: $\forall t \qdot \ran(\mathit{tag}_t) \cap \mathit{COMMON} = \empty$

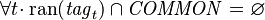
The above-mentioned scope-restricting hypothesis can be reformulated into: 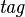$\mathit{tag}$ needs not be stable across sessions nor across platforms.

Formula Factory

The requirements about tags give rise to a need for centralising the 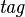$\mathit{tag}$ relation in order to enforce tag uniqueness. The Formula Factory appears to be a convenient and logical candidate for playing this role. Each time an extension is used to make a formula, the factory is called and it can check whether its associated tag exists, create it if needed, then return the new extended formula while maintaining tag consistency.

The factory can also provide API for requests about tags and extensions: getting the tag from an extension and conversely.

Impact on other tools

Impacted plug-ins (use a factory to build formulæ):

• org.eventb.core

In particular, the static checker and proof obligation generator are impacted.

• org.eventb.core.seqprover
• org.eventb.pp
• org.eventb.pptrans
• org.eventb.ui

Identified Problems

The parser shall enforce verifications to detect the following situations:

• Two mathematical extensions are not compatible (the extensions define symbols with the same name but with a different semantics).
• A mathematical extension is added to a model and there is a conflict between a symbol and an identifier.
• An identifier which conflicts with a symbol of a visible mathematical extension is added to a model.

Beyond that, the following situations are problematic:

• A formula has been written with a given parser configuration and is read with another parser configuration.

As a consequence, it appears as necessary to remember the parser configuration.

The static checker will then have a way to invalid the sources of conflicts (e.g., priority of operators, etc).

The static checker will then have a way to invalid the formula upon detecting a conflict (name clash, associativity change, semantic change...) mathieu

• A proof may free a quantified expression which is in conflict with a mathematical extension.

SOLUTION #1: Renaming the conflicting identifiers in proofs?

Open Questions

New types

Which option should we prefer for new types?

• OPTION #1: Transparent mode.

In transparent mode, it is always referred to the base type. As a consequence, the type conversion is implicitly supported (weak typing).

For example, it is possible to define the DISTANCE and SPEED types, which are both derived from the 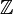$\intg$ base type, and to multiply a value of the former type with a value of the latter type.

• OPTION #2: Opaque mode.

In opaque mode, it is never referred to the base type. As a consequence, values of one type cannot be converted to another type (strong typing).

Thus, the above multiplication is not allowed.

This approach has at least two advantages:

• Stronger type checking.
• Better prover performances.

It also has some disadvantages:

• need of extractors to convert back to base types.
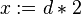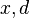• need of extra circuitry to allow things like $x:=d*2$ where $x, d$ are of type DISTANCE

• OPTION #3: Mixed mode.

In mixed mode, the transparent mode is applied to scalar types and the opaque mode is applied to other types.

Scope of the mathematical extensions

• OPTION #1: Project scope.

The mathematical extensions are implicitly visible to all components of the project that has imported them.

• OPTION #2: Component scope.

The mathematical extensions are only visible to the components that have explicitly imported them. However, note that this visibility is propagated through the hierarchy of contexts and machines (EXTENDS, SEES and REFINES clauses).

An issue has been identified. Suppose that ext1 extension is visible to component C1 and ext2 is visible to component C2, and there is no compatibility issue between ext1 and ext2. It is not excluded that an identifier declared in C1 conflict with a symbol in ext2. As a consequence, a global verification is required when adding a new mathematical extension.

Bibliography

• J.R. Abrial, M.Butler, M.Schmalz, S.Hallerstede, L.Voisin, Proposals for Mathematical Extensions for Event-B, 2009.

This proposal consists in considering three kinds of extension:

1. Extensions of set-theoretic expressions or predicates: example extensions of this kind consist in adding the transitive closure of relations or various ordered relations.
2. Extensions of the library of theorems for predicates and operators.
3. Extensions of the Set Theory itself through the definition of algebraic types such as lists or ordered trees using new set constructors.