ADVANCE D3.3 Model Checking

Overview

We think that animation and model checking are important tools when building a model. Animation allows the user to validate if the model corresponds to the user's intentions. Model checking allows to check if the model contains errors and provides counter-examples that help to understand the problem beforehand. Moreover, it allows to reason with domains (like physical units) and verify some properties (like temporal logic ones), that have currently no matching proof support. The following activities were pursued within the project:

• The constraint solving capabilities of ProB have been continuously improved along with scalability improvements.
• Previously we implemented a TLA to B compiler to use ProB on TLA⁺ specifications. We now also support the direction from B to TLA⁺. This allows to use the TCL model checker on B specifications.
• There is work in progress towards support of the upcoming 2.0 version of the Theory plug-in.
• We are working on a secondary independent toolchain for animation.
• We finalized and released the of physical units plug-in.

Outside ADVANCE we improved the model checker by adding support for distributed model checking, partial order reduction and partial guard evaluation. We think that these improvements are also valuable within the ADVANCE project.

Motivations / Decisions

Secondary toolchain

Independently of ProB we completed the development of a tool, which is able read solutions (constant and variable-values) generated by ProB and evaluate predicates like the properties or the invariant of a B model. Also it is possible to evaluate expression in an interactive mode or animate B machines. The tool is (with the exception of the parser) a complete new implementation of a predicate/expression B-evaluator and animator in python. The goal of the reimplementation is to establish a second independent toolchain to crosscheck results of ProB. The python tool has been successfully tested with industrial B Models from the railway domain. The tool is available from http://github.com/hhu-stups/pyB

B to TLA⁺

We developed a transcompiler from B to TLA⁺ (Temporal Logic of Actions) to verify B specifications with TLC. TLC is an explicit state model checker for TLA⁺ with an efficient disk-based algorithm and support for temporal formulas and fairness.Our translator is full automatic and supports a large subset of B. Moreover it uses static analyses to verify the correctness of the B specification (e.g. type checking and scope checking) and creates an optimized translation for the validation with TLC. Error traces (e.g. leading to deadlocks or invariant violations) detected by TLC are translated back to B and can be verified by ProB.

TODO Kodkod Currently the translation to Kodkod is only applied to axioms when trying to find values for the constants and during the constraint based deadlock check. We plan to restructure ProB's internal programming interfaces in a way that allows to apply Kodkod more easily and make it available for other checks (e.g. constraint-based invariant check, assertion checks). We will evaluate how we can employ more SMT based techniques in ProB.

TODO Constraint Solver Improvements During the further development of ProB's constraint solving it became apparent that it would be helpful to represent the cardinality of a set by a CLP(FD) variable. We plan to change ProB's internal representation of sets in a way that its cardinality can be accessed in this way. To allow a translation from ProB to Kodkod, we implemented an integer interval analysis. We plan to adapt the analysis to set up sizes of deferred sets. This is necessary because ProB chooses a fixed size for a deferred set and sometimes a model has only solutions for a certain size. Currently a user must supply a size manually.

Theory Plug-in support

We adapted ProB to the changes that had been made to the Theory Plug-in in preperation of the upcoming release. We implemented support for the theory of transitive closures. From the current set of standard theories, ProB supports animation of models that use operators of the theories "BoolOps", "FixPoint", "Seq", "SUMandPRODUCT" and "closure". Still unsupported are the operators of the remaining standard theories "BinaryTree" and "List" which use recursively defined operators. We plan to implement support for them for the next release.

LTL Fairness

We currently explore ways to implement Fairness into ProB's LTL model checker. However, it is already possible to use fairness by using the B to TLA translator and running TLC.

Physical Units

The work on physical unit support has been completed and is available as an optional plug-in available from the ProB update site.

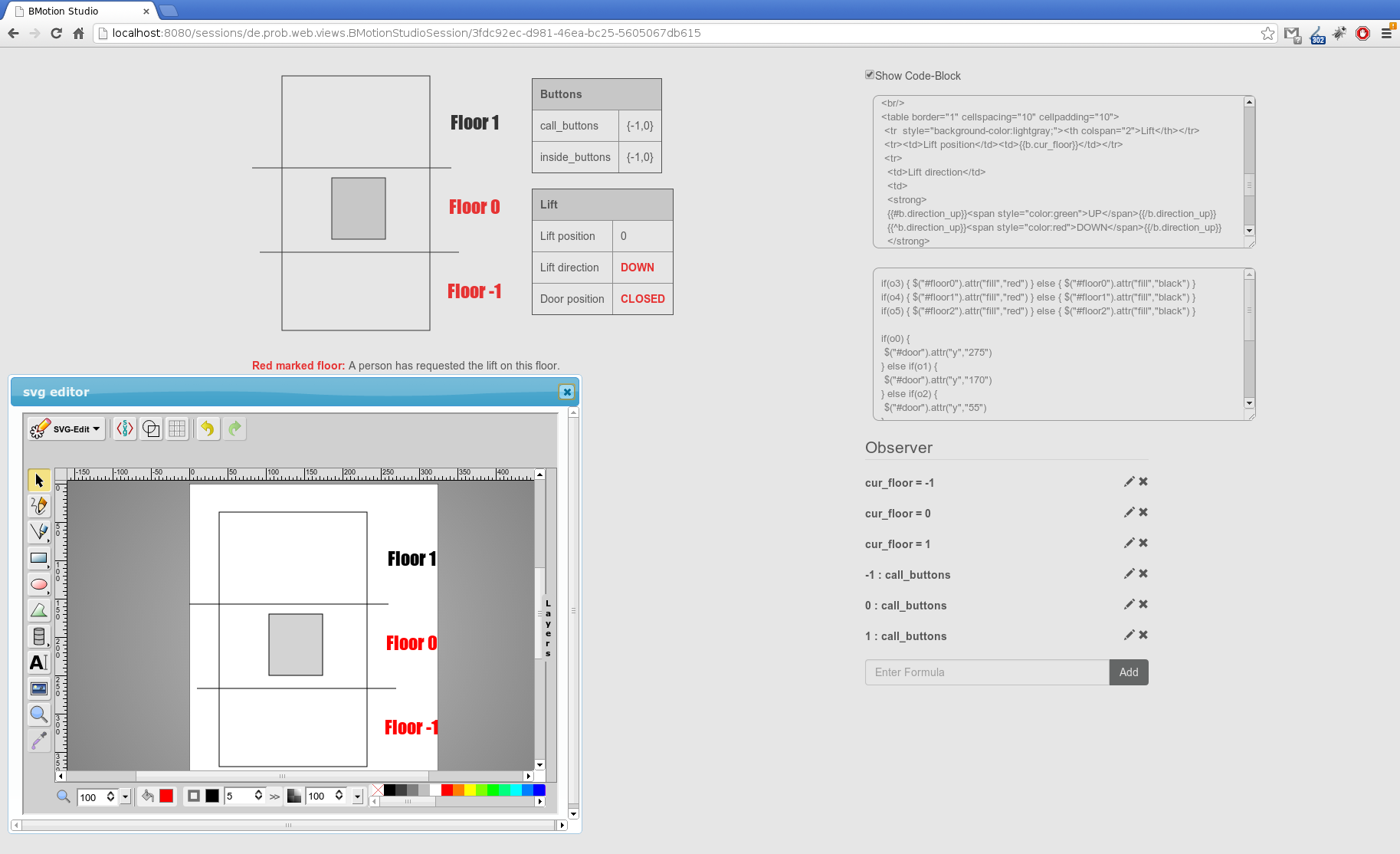
BMotion Studio

BMotion Studio provides an easy and fast way to create a visualization for a formal model. It comes with a set of predefined widgets and observer which are sufficient for most visualizations. However, it is still cumbersome to add custom widgets and observer to BMotion Studio, since the user needs programming skills in Java and Eclipse Plugin Development. As a consequence we decided to replace the rendering-engine of BMotion Studio with HTML. This has the benefit that we can use the entire HTML functionality. For instance, HTML elements like tables, buttons and images as well as features like CSS (Cascading Style Sheets) and SVG (Scalable Vector Graphics). In addition, the user can reuse all HTML snippets which can be found in the WWW for his own visualization. While the user can create visualizations by writing HTML or SVG, we will also provide a way to create visualizations as in the old BMotion Studio, i.e. via a visual editor with easy to use dialogues and wizards.

Available Documentation

ProB
The ProB Website is the place where we collect information on the ProB toolset. There are several tutorials on ProB available in the User manual section. We also supply documentation on extending ProB for developers.

In addition we run a bug tracking system to document known bugs, workarounds and feature requests.

BMotion Studio
A developer-, user documentation, tutorial and examples are available from a dedicated webpage hosted by the University of Duesseldorf.

Planning

TODO