Mathematical Extensions

Currently the operators and basic predicates of the Event-B mathematical language supported by Rodin are fixed. We propose to extend Rodin to define basic predicates, new operators or new algebraic types.

Requirements

Usage Requirements

• Binary operators (prefix form, infix form or suffix form).
• Operators on boolean expressions.
• Unary operators, such as absolute values.

Note the the pipe, which is already used for set comprehension, cannot be used to enter absolute values.

• Basic predicates (e.g., the symmetry of relations $sym(R) \defi R=R^{-1}$).

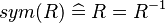Having a way to enter such predicates may be considered as syntactic sugar, because it is already possible to use sets (e.g., 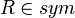$R \in sym$, where 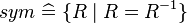$sym \defi \{R \mid R=R ^{-1}\}$) or functions (e.g., 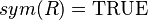$sym(R) = \True$, where $sym \defi \lambda(R) \qdot (R \in A \rel B \mid \bool(R = R^{-1}))$).

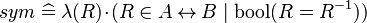• Quantified expressions (e.g., $\sum x \qdot (P \mid y)$, $\prod x \qdot (P \mid y)$, $~\min(S)$, $~\max(S)$).

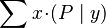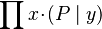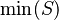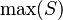Development Requirements

• Scalable developments.
• The end-user shall provide the following information:
  • Typing rules.
  • Well-definedness.
  • Notation.

More precisely, the form (prefix, infix, postfix), the set of symbols, the syntax, the mode (flattened or not), ... shall be entered.

• • Pretty-print.

Alternatively, the rendering may be determined from the notation parameters passed to the parser.

• • Pre-conditions.

Towards a generic AST

The following AST parts are to become generic, or at least parameterised:

• Lexer
• Parser
• Nodes ( Formula class hierarchy ): parameters needed for:
  • Type Solve (type rule needed to synthesize the type)
  • Type Check (type rule needed to verify constraints on children types)
  • WD (WD predicate)
  • PrettyPrint (tag image + notation (prefix, infix, postfix))
  • Visit Formula (getting children + visitor callback mechanism)
  • Rewrite Formula (associative formulæ have a specific flattening treatment)
• Types (Type class hierarchy): parameters needed for:
  • Building the type expression (type rule needed)
  • PrettyPrint (set operator image)
  • getting Base / Source / Target type (type rule needed)
• Formula Factory

Impact on other tools

Impacted plug-ins (use a factory to build formulæ):

• org.eventb.core
• org.eventb.core.seqprover
• org.eventb.pp
• org.eventb.pptrans
• org.eventb.ui

Bibliography

• J.R. Abrial, M.Butler, M.Schmalz, S.Hallerstede, L.Voisin, Proposals for Mathematical Extensions for Event-B, 2009.

This proposal consists in considering three kinds of extension:

1. Extensions of set-theoretic expressions or predicates: example extensions of this kind consist in adding the transitive closure of relations or various ordered relations.
2. Extensions of the library of theorems for predicates and operators.
3. Extensions of the Set Theory itself through the definition of algebraic types such as lists or ordered trees using new set constructors.