imported>Alexili |
imported>Alexili |
| (16 intermediate revisions by the same user not shown) |
| Line 1: |
Line 1: |
| − | == Flows plugin ==
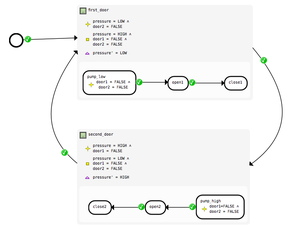
| + | The Flow plug in is a Rodin Platform extension assisting in the formulation of verification conditions related to the dynamic properties of a model, i.e., event ordering and enabledness conditions. A visual notation is used to define graph-like structures that are translated into Event-B theorems (for efficiency reasons, these appear as machine proof obligations). The tool simplifies a number of routine tasks such as writing and maintaining deadlock-freedom and relative deadlock freedom proof obligations. Its core functionality is concerned with the verification of the feasibility of use case scenarious: checking that certain event paths are feasible for a given model. |
| | | | |
| − | ----
| + | [[Image:Flow_doors.png|thumb|right|Sample flow diagram]] |
| | + | |
| | | | |
| − | Event-B, being an event systems formalism does not have a mechanism for explicitly defining event ordering. Although event guards may express any desired event ordering, the ability to have a summary of possible event flows in a concise and compact form is useful for many tasks, for example, code generation and connecting with other formalisms. The flows plugin addresses one aspect of event ordering: it allows a modeller to specify and prove that a given sequence of events does not contradict a given machine specification. More precisely, if we were to execute a machine step-by-step following our prescribed sequence of events we would not discover divergencies and deadlocks not already present in the original machine. In other words, the constraining of event ordering must be such that the overall specification is an Event-B refinement of the original model. Importantly, this means that all the desired model properties proved before are preserved.
| |
| | | | |
| − | Sequential composition of events may be expressed in a number of ways:
| + | ==== Flow diagram ==== |
| | | | |
| − | * event immediately follows another event; no other events may take place between the composed events.
| + | The nodes of a flow diagram are events, possibly constrained with additional predicates; its edges are ''event relations''. There are three kinds of event relations - enabling, disabling, feasibility. The event relations state the relationship between the after-state of one event and the enabling condition of the other. A flow diagram should not be confused with a state diagram or a workflow graph. The only effect of a flow diagram is the generation of additional verification; it has no behavioral semantics and does not constrain machine behaviour. |
| − | * event eventually follows an event; thus, although there is an interference from other events, it is guaranteed that the second is eventually enabled.
| |
| − | * event may follow an event; this is the weakest form of connection when we only say that it may be the case that the second event follows the first event; it may happen, however, that some other event interferes and the second event is delayed or is even not enabled ever.
| |
| | | | |
| − | === The Flows Approach ===
| |
| | | | |
| − | Although the last case may seem the least appealing, it is the one that forms the basis of the flows approach. The primary reason for offering such a weak guarantee is proof effort required for stronger types of connectives. Let us see what it means to provide a formal proof for the various cases of sequential event composition.
| + | ===== Enabling relation ===== |
| | | | |
| − | <math>e_2</math> "immediately after" <math>e_1</math> requires, among others, the demonstration of a condition that no event other than <math>e_2</math> is enabled in the after-state of <math>e_1</math>. This leads to <math>n</math> proof obligations where <math>n</math> is the number of machine events. This number of proof obligations is comparable to the effort of demonstrating machine consistency. For a flow expression mentioning "immediately after" <math>m</math> times there would be <math>m*n</math> proof obligations. Even if only a small fraction of these result in interactive proofs, it would still be impractical for any realistic model.
| + | The enabling relation expresses that an event ''may follow'' some other event. More precisely, it requires that the guard of the event at the target of the relation edge is enabled after the execution of the event at the source of the edge. It is not guaranteed that the target event is executed immediately or eventually after the source event. The interference from other events may temporarily or permanently disable the target event even though it was momentarily enabled in the after-state of the first event. Below is an example of a flow diagram using the enabling relation. |
| | | | |
| − | For the second case, where <math>e_2</math> "eventually follows" <math>e_1</math>, one has to prove that an overall effect of any possible interference between the occurrence of <math>e_1</math> and <math>e_2</math> is such that the resultant state is a sub-state of states where <math>e_2</math> is enabled. Seeing all other events as relations on machine state and assuming they are already proved convergent, the effect of event interference is represented by a transitive closure of a disjunction of all interference relations. The result is a rather expensive proof obligation that, almost certainly, would require a manual proof.
| + | [[Image:model1aa.png|center|450px|border]] |
| | | | |
| − | Contrastingly, the last case - <math>e_2</math> "may follow" <math>e_1</math> - requires one simple proof obligation that, in most cases, would be discharged without a user assistance: the after-state of <math>e_1</math> should imply the guard of <math>e_2</math>. We denote this condition as <math>PO(e_1;e_2)</math>. This style of sequential composition used in the flows method and the following shortcut notation is offered: <math>e_1; e_2</math> (note the events order).
| + | Circle denotes the initialisation event; circle with a block dot is an implicit termination (or deadlock) event. The latter is defined as event with no actions and a guard formed by negating of the disjunction of the guards of all the model events (not including skip, initialisation and the termination events). |
| | | | |
| − | One generalisation of <math>e_1;e_2</math> is having a vector of events on the right-hand side: <math>e_1;(e_2, e_3, \dots, e_n)</math>. It is easy to see how to scale up the proof obligation for this case. Then,
| + | When for a node there is more than one outgoing relation of a given kind it is enough to satisfy any one of the relations. For the enabling relation, this expresses the internal choice on event firings. There are annotations, discussed further, overriding this interpretation. |
| − | <math>PO(e_1;(e_2, e_3, \dots, e_n)) = PO(e_1;e_2) \lor PO(e_1;e_3) \lor \dots \lor PO(e_1;e_n)</math>.
| |
| | | | |
| − | The meaning of this extended construct is quite straightforward: there is a choice of possible continuation events after some current event <math>e_1</math>. Further, we use the following notation for <math>e_1;(e_2, e_3, \dots, e_n)</math>: <math>e_1;(e_2 | e_3 | \dots | e_n)</math> where <math>a | b</math> reads as "a choice of <math>a</math> and <math>b</math>". Note that expression <math>e_1 | e_2</math> is not well-formed on its own. Choice of events has a meaning only in a combination with operator <math>;</math>.
| |
| | | | |
| − | A flow expression is a list of statements about event ordering.
| + | Sample diagram given above defines four theorems. There is a theorem stating that event ''e1'' is enabled right after the initialisation (the proof obligation name is INITIALISATION/e1/FENA where the suffix ''FENA'' stands for Flow ENABledness proof obligations; this suffix is always used with enabling relation) a theorem showing that ''e1'' enables ''e2'' or ''e3'' or both (the proof obligation name is e1/e2:e3/FENA and reads "after e1, e2 or e3 is enabled"; a theorem showing that after 'e3' the system terminates and, finally, a theorem for the enabledness of ''e1'' after the execution of ''e2''. The following is an screenshot from the tool showing the annotated diagram and proof status. Proof statuses are updated along with the progress of the Rodin builder and provers and thus there will be always some delays between saving a diagram and proof status update. |
| | | | |
| − | <math>e_1;(n_1 | \dots | n_i)</math>
| + | [[Image:Model1a.png|center|450px|border]] |
| | + | |
| | + | A double-click on edge would automatically open the relevant proof obligation in the interactive prover. |
| | | | |
| − | <math>e_2;(m_1 | \dots | m_j)</math>
| |
| | | | |
| − | <math>\dots</math>
| |
| | | | |
| − | <math>e_k;(t_1 | \dots | t_l)</math>
| + | ===== Disabling relation ===== |
| | | | |
| − | The semantics of each such statement is already given above: it is a theorem expressing requirements to the events mentioned in a statement. More precisely, it is an additional proof obligation for machine for which the flow statements are defined. Note that there is no obligation to mention all the machine events in a flow expression. | + | The disabling relation is the opposite of the enabling relation: it requires that the target event is not enabled after the execution of a source event. |
| | | | |
| − | How expressive is the language of flows? There is, effectively, just one construct but it already covers a form of sequential composition, choice and loop. A loop is expressed by adding a statement to pass control back the beginning of the loop body:
| + | ==== Update site ==== |
| | | | |
| − | <math>b_1;b_2</math>
| + | Use the following update site to install and update the plug in. |
| − | <math>b_2;b_3</math>
| |
| − | <math>b_3;b_1</math>
| |
| | | | |
| − | The above is a loop made of a sequential composition of three events <math>b_1, b_2, b_3</math>.
| + | http://iliasov.org/usecase |
| | | | |
| − | ==== Concurrency ====
| |
| − | One important notion missing in the flows language is event concurrency. And here again, the concept of passing control from one event to another (operator <math>;</math>) plays the central role. First, we note that concurrency is linked to the idea of a thread of a control. In other words, to define <math>m</math> events as executing concurrently there must be at least <math>m</math> threads of control. Another observation is that there should be a way to start (or unblock) and terminate (block) a thread. In this case, by starting a thread we understanding passing a control to a continuation that has one additional thread of control (an alternative is having all threads started by an initialisation and then being unblocked and blocked when necessary). Correspondingly, termination of thread is a continuation that has one less thread of control. Terminating the last thread is the termination of the whole system.
| |
| − |
| |
| − | To construct a new thread, some current tread is split into two threads. In Event-B terms, this corresponds to passing the control from an event to a pair of events such that they may execute in any order, that is, hey are both enabled and do not assign to the same model variables. We call such events independent. Let <math>t_1</math> and <math>t_2</math> be some distinct independent events. Then notation <math>e;t_1 \| t_2</math> states that after <math>e</math> both <math>t_1</math> and <math>t_2</math> are enabled. <math>t_1 \| t_2</math> reads as "<math>t_1</math> concurrently with <math>t_2</math>". The semantics of this construct is quite simple:
| |
| − | <math>PO(e;t_1 \| t_2) = PO(e;t_1) \land PO(e;t_2)</math>.
| |
| − |
| |
| − | Thread termination is a symmetric case of thread creation. Concurrent events appear on the left-hand side of a sequential composition with an event: <math>t_1 \| t_2; e</math>. The meaning of this construct is that once <math>t_1</math> and <math>t_2</math> stopped, <math>e</math> is enabled. Since <math>t_1</math> and <math>t_2</math> are independent, it is enough to separately demonstrate that <math>t_1</math> enables <math>e</math> and <math>t_2</math> enables <math>e</math>: <math>PO(t_1 \| t_2;e) = PO(t_1;e) \land PO(t_2;e)</math>.
| |
| − |
| |
| − | The way we have defined thread construction does not make it clear how to define a thread that starts with a choice of events, for example <math>a | b, b;d</math>. This limitation, however, is easy to overcome by noticing that the skip event may be used to reduce the case of a thread starting with a choice to thread that has a single initial event: <math>skip;(a | b), b;d</math>. Since <math>skip</math> does no alter state, the overall behaviour is the same. This way, we are able to treat a general case:
| |
| − |
| |
| − | <math>e;(f_1 | \dots | f_k) \| (g_1 | \dots | g_l)</math>
| |
| − |
| |
| − | The semantics of the construct is defined as follows:
| |
| − |
| |
| − | <math>
| |
| − | \begin{array}{l}
| |
| − | PO(e;(f_1 | \dots | f_k) \| (g_1 | \dots | g_l)) = \\
| |
| − | \qquad PO(e;(f_1 | \dots | f_k)) \land PO(e;(g_1 | \dots | g_l)) = \\
| |
| − | \qquad \qquad (PO(e;f_1) \lor \dots PO(e;f_k)) \land (PO(e;g_1) \lor \dots PO(e;g_l))
| |
| − | \end{array}
| |
| − | </math>
| |
| − |
| |
| − | The same thinking is applied to thread termination case. For a more readable notation, the sequential composition operation may be generalised to an associative version:
| |
| − | <math>a;b;c</math>
| |
| − |
| |
| − | The above simply stands for <math>a;b, b;c</math>. It is also easy to see how to scale this up to for the case of choice construct. However, loop <math>a;b, b;a</math> would be defined as - using a new operator * - <math>*(a;b)</math> rather than <math>a;b;a</math>. The is due to the fact that we want to be able to make a distinction between an event of a model and an event of a flow expression. Such a generalisation makes it possible to include the same event more than once in a flow expression and define event parameters in flows.
| |
| − |
| |
| − | To account for event parameter, the basic PO rule <math>PO(e_1;e_2)</math> is now extended to accept two parameters: <math>PO(e_1;e_2, P, Q)</math>. Here, <math>P</math> and <math>Q</math> are predicates defined on model variables and also on the parameters of their respective events. <math>P</math> and <math>Q</math> are, essentially, additional event guards and that is also how they appear in a proof obligation.
| |
| − |
| |
| − | ==== Event Compositionality PO ====
| |
| − | Finally, we give a formal definition of <math>PO(e_1;e_2, P, Q)</math>. Remember, that <math>e_1;e_2</math> was defined as ''an event may follow another event''. A way to formally demonstrate this is to show that an after-state of the first event always enables the guard of the next event.
| |
| − |
| |
| − | <math>PO(e_1;e_2, P, Q) \equiv I(v) \land G(p, v) \land P(p, v) \land S(p, v, v') \implies Q(r, v) \land H(r, v)</math>
| |
| − |
| |
| − | where <math>p</math> and <math>r</math> are the parameters of the first and the second event, correspondingly. <math>G</math> and <math>S</math> are the guard and before-after predicate of the first event whereas <math>H</math> is the guard of the second event. <math>I</math> is the model invariant and <math>P</math> and <math>Q</math> are the parameter constraining predicates from a flow expression.
| |
| | | | |
| | | | |
| | + | === See also === |
| | | | |
| | + | [[Old Flow Plug in page]] |
| | | | |
| | | | |
| | | | |
| | [[Category:Plugin]] | | [[Category:Plugin]] |
The Flow plug in is a Rodin Platform extension assisting in the formulation of verification conditions related to the dynamic properties of a model, i.e., event ordering and enabledness conditions. A visual notation is used to define graph-like structures that are translated into Event-B theorems (for efficiency reasons, these appear as machine proof obligations). The tool simplifies a number of routine tasks such as writing and maintaining deadlock-freedom and relative deadlock freedom proof obligations. Its core functionality is concerned with the verification of the feasibility of use case scenarious: checking that certain event paths are feasible for a given model.
Flow diagram
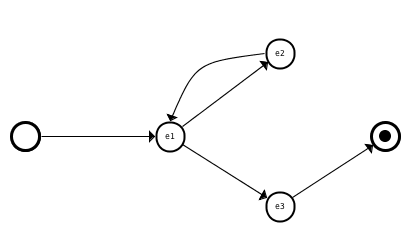
The nodes of a flow diagram are events, possibly constrained with additional predicates; its edges are event relations. There are three kinds of event relations - enabling, disabling, feasibility. The event relations state the relationship between the after-state of one event and the enabling condition of the other. A flow diagram should not be confused with a state diagram or a workflow graph. The only effect of a flow diagram is the generation of additional verification; it has no behavioral semantics and does not constrain machine behaviour.
Enabling relation
The enabling relation expresses that an event may follow some other event. More precisely, it requires that the guard of the event at the target of the relation edge is enabled after the execution of the event at the source of the edge. It is not guaranteed that the target event is executed immediately or eventually after the source event. The interference from other events may temporarily or permanently disable the target event even though it was momentarily enabled in the after-state of the first event. Below is an example of a flow diagram using the enabling relation.
Circle denotes the initialisation event; circle with a block dot is an implicit termination (or deadlock) event. The latter is defined as event with no actions and a guard formed by negating of the disjunction of the guards of all the model events (not including skip, initialisation and the termination events).
When for a node there is more than one outgoing relation of a given kind it is enough to satisfy any one of the relations. For the enabling relation, this expresses the internal choice on event firings. There are annotations, discussed further, overriding this interpretation.
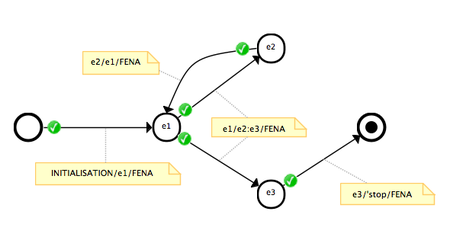
Sample diagram given above defines four theorems. There is a theorem stating that event e1 is enabled right after the initialisation (the proof obligation name is INITIALISATION/e1/FENA where the suffix FENA stands for Flow ENABledness proof obligations; this suffix is always used with enabling relation) a theorem showing that e1 enables e2 or e3 or both (the proof obligation name is e1/e2:e3/FENA and reads "after e1, e2 or e3 is enabled"; a theorem showing that after 'e3' the system terminates and, finally, a theorem for the enabledness of e1 after the execution of e2. The following is an screenshot from the tool showing the annotated diagram and proof status. Proof statuses are updated along with the progress of the Rodin builder and provers and thus there will be always some delays between saving a diagram and proof status update.
A double-click on edge would automatically open the relevant proof obligation in the interactive prover.
Disabling relation
The disabling relation is the opposite of the enabling relation: it requires that the target event is not enabled after the execution of a source event.
Update site
Use the following update site to install and update the plug in.
http://iliasov.org/usecase
See also
Old Flow Plug in page