Inference Rules: Difference between revisions
From Event-B
Jump to navigationJump to search
imported>Laurent m Marked rule FUN_IMAGE_GOAL as implemented |
imported>Laurent m Marked rules ONE_POINT_L and ONE_POINT_R as implemented |
||
| Line 195: | Line 195: | ||
{{RRRow}}|*||{{Rulename|DISTINCT_CASE}}|| <math>\frac{\textbf{H} \;\;\vdash \;\; {WD}(\textbf{P}) \qquad \textbf{H}, {WD}(\textbf{P}), \textbf{P} \;\;\vdash \;\; \textbf{\textbf{G}} \qquad \textbf{H}, {WD}(\textbf{P}), \lnot \textbf{P} \;\;\vdash \;\; \textbf{G}}{\textbf{H} \;\;\vdash\;\; \textbf{G}}</math> || case distinction on predicate <math>\textbf{P}</math> || M | {{RRRow}}|*||{{Rulename|DISTINCT_CASE}}|| <math>\frac{\textbf{H} \;\;\vdash \;\; {WD}(\textbf{P}) \qquad \textbf{H}, {WD}(\textbf{P}), \textbf{P} \;\;\vdash \;\; \textbf{\textbf{G}} \qquad \textbf{H}, {WD}(\textbf{P}), \lnot \textbf{P} \;\;\vdash \;\; \textbf{G}}{\textbf{H} \;\;\vdash\;\; \textbf{G}}</math> || case distinction on predicate <math>\textbf{P}</math> || M | ||
{{RRRow}}| ||{{Rulename|ONE_POINT_L}}||<math>\frac{\textbf{H} \;\;\vdash \;\; {WD}(E) \qquad \textbf{H}, \forall x, \ldots, \ldots,z \qdot [y \bcmeq E]\textbf{P} \land \ldots \land \ldots \land [y \bcmeq E]\textbf{Q} \limp [y \bcmeq E]\textbf{R} \;\;\vdash \;\; \textbf{G}}{ \textbf{H}, \forall x, \ldots, y, \ldots, z \qdot \textbf{P} \land \ldots \land y = E \land \ldots \land \textbf{Q} \limp \textbf{R} \;\;\vdash\;\; \textbf{G}}</math>|| The rule can be applied with <math>\forall</math> as well as with <math>\exists</math> || A | {{RRRow}}|*||{{Rulename|ONE_POINT_L}}||<math>\frac{\textbf{H} \;\;\vdash \;\; {WD}(E) \qquad \textbf{H}, \forall x, \ldots, \ldots,z \qdot [y \bcmeq E]\textbf{P} \land \ldots \land \ldots \land [y \bcmeq E]\textbf{Q} \limp [y \bcmeq E]\textbf{R} \;\;\vdash \;\; \textbf{G}}{ \textbf{H}, \forall x, \ldots, y, \ldots, z \qdot \textbf{P} \land \ldots \land y = E \land \ldots \land \textbf{Q} \limp \textbf{R} \;\;\vdash\;\; \textbf{G}}</math>|| The rule can be applied with <math>\forall</math> as well as with <math>\exists</math> || A | ||
{{RRRow}}| ||{{Rulename|ONE_POINT_R}}||<math>\frac{\textbf{H} \;\;\vdash \;\; {WD}(E) \qquad \textbf{H} \;\;\vdash \;\; \forall x, \ldots, \ldots,z \qdot [y \bcmeq E]\textbf{P} \land \ldots \land \ldots \land [y \bcmeq E]\textbf{Q} \limp [y \bcmeq E]\textbf{R} }{ \textbf{H} \;\;\vdash\;\; \forall x, \ldots, y, \ldots, z \qdot \textbf{P} \land \ldots \land y = E \land \ldots \land \textbf{Q} \limp \textbf{R} }</math>|| The rule can be applied with <math>\forall</math> as well as with <math>\exists</math> || A | {{RRRow}}|*||{{Rulename|ONE_POINT_R}}||<math>\frac{\textbf{H} \;\;\vdash \;\; {WD}(E) \qquad \textbf{H} \;\;\vdash \;\; \forall x, \ldots, \ldots,z \qdot [y \bcmeq E]\textbf{P} \land \ldots \land \ldots \land [y \bcmeq E]\textbf{Q} \limp [y \bcmeq E]\textbf{R} }{ \textbf{H} \;\;\vdash\;\; \forall x, \ldots, y, \ldots, z \qdot \textbf{P} \land \ldots \land y = E \land \ldots \land \textbf{Q} \limp \textbf{R} }</math>|| The rule can be applied with <math>\forall</math> as well as with <math>\exists</math> || A | ||
|} | |} | ||
Revision as of 13:47, 16 November 2010
CAUTION! Any modification to this page shall be announced on the User mailing list!
Rules that are marked with a * in the first column are implemented in the latest version of Rodin. Rules without a * are planned to be implemented in future versions. Other conventions used in these tables are described in The_Proving_Perspective_(Rodin_User_Manual)#Inference_Rules.
| Name | Rule | Side Condition | A/M
| |
|---|---|---|---|---|
| * | HYP |
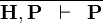 |
A
| |
| * | HYP_OR |
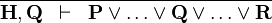 |
A
| |
| * | CNTR |
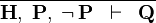 |
A
| |
| * | FALSE_HYP |
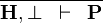 |
A
| |
| * | TRUE_GOAL |
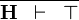 |
A
| |
| * | FUN_GOAL |
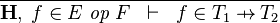 |
where 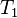 and and 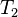 denote types and denote types and 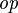 is one of is one of 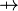 , , 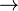 , , 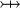 , , 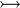 , , 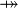 , , 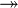 , , 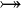 . . |
A
|
| * | FUN_IMAGE_GOAL |
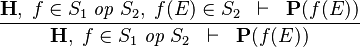 |
where 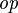 denotes a set of relations (any arrow) and denotes a set of relations (any arrow) and 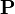 is WD strict is WD strict |
M
|
FUN_GOAL_REC |
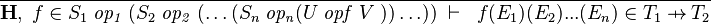 |
where 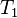 and and 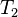 denote types, denote types, 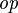 denotes a set of relations (any arrow) and denotes a set of relations (any arrow) and 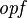 is one of is one of 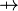 , , 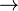 , , 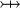 , , 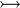 , , 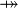 , , 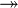 , , 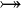 . . |
A
| |
| * | DBL_HYP |
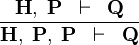 |
A
| |
| * | AND_L |
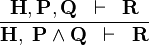 |
A
| |
| * | AND_R |
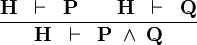 |
A
| |
IMP_L1 |
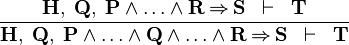 |
A
| ||
| * | IMP_R |
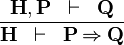 |
A
| |
| * | IMP_AND_L |
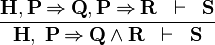 |
A
| |
| * | IMP_OR_L |
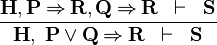 |
A
| |
| * | AUTO_MH |
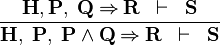 |
A
| |
| * | NEG_IN_L |
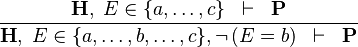 |
A
| |
| * | NEG_IN_R |
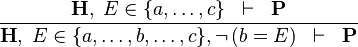 |
A
| |
| * | XST_L |
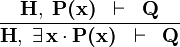 |
A
| |
| * | ALL_R |
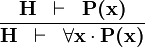 |
A
| |
| * | EQL_LR |
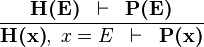 |
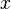 is a variable which is not free in is a variable which is not free in 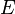 |
A
|
| * | EQL_RL |
 |
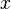 is a variable which is not free in is a variable which is not free in 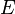 |
A
|
SUBSET_INTER |
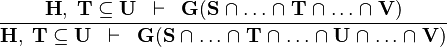 |
where 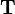 and and 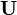 are not bound by are not bound by 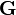 |
A
| |
IN_INTER |
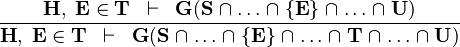 |
where 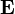 and and 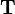 are not bound by are not bound by 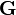 |
A
| |
NOTIN_INTER |
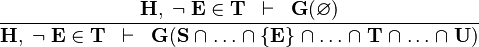 |
where 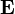 and and 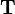 are not bound by are not bound by 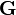 |
A
| |
| * | FIN_L_LOWER_BOUND_L |
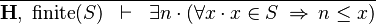 |
The goal is discharged | A
|
| * | FIN_L_LOWER_BOUND_R |
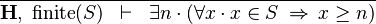 |
The goal is discharged | A
|
| * | FIN_L_UPPER_BOUND_L |
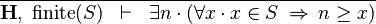 |
The goal is discharged | A
|
| * | FIN_L_UPPER_BOUND_R |
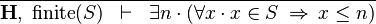 |
The goal is discharged | A
|
| * | CONTRADICT_L |
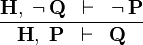 |
M
| |
| * | CONTRADICT_R |
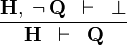 |
M
| |
| * | CASE |
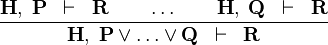 |
M
| |
| * | MH |
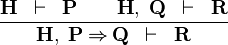 |
M
| |
| * | HM |
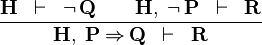 |
M
| |
EQV |
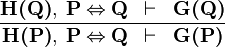 |
M
| ||
| * | OV_SETENUM_L |
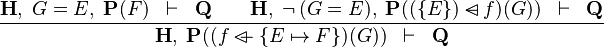 |
where 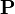 is WD strict is WD strict |
A
|
| * | OV_SETENUM_R |
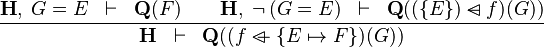 |
where 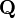 is WD strict is WD strict |
A
|
| * | OV_L |
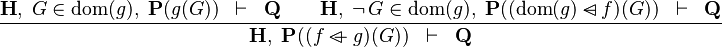 |
where 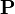 is WD strict is WD strict |
A
|
| * | OV_R |
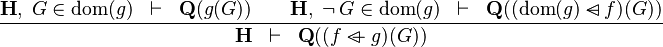 |
where 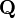 is WD strict is WD strict |
A
|
| * | DIS_BINTER_R |
![\frac{\textbf{H} \;\;\vdash\;\; f^{-1} \in A \pfun B \qquad\textbf{H} \;\;\vdash\;\;\textbf{Q}(f[S] \binter f[T]) }{\textbf{H} \;\;\vdash \;\; \textbf{Q}(f[S \binter T])}](/images/math/0/3/8/0385bdd4c9cd892d9cf7289b1de32a3c.png) |
where 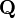 is WD strict, is WD strict, 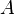 and and 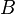 denote types. denote types. |
M
|
| * | DIS_BINTER_L |
![\frac{\textbf{H} \;\;\vdash\;\; f^{-1} \in A \pfun B \qquad\textbf{H},\;\textbf{Q}(f[S] \binter f[T]) \;\;\vdash\;\;\textbf{G}}{\textbf{H},\; \textbf{Q}(f[S \binter T]) \;\;\vdash \;\; \textbf{G}}](/images/math/1/3/f/13f3f5de8aa0fbd38b361bdbeb350c47.png) |
where 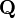 is WD strict, is WD strict, 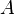 and and 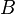 denote types. denote types. |
M
|
| * | DIS_SETMINUS_R |
![\frac{\textbf{H} \;\;\vdash\;\; f^{-1} \in A \pfun B \qquad\textbf{H} \;\;\vdash\;\;\textbf{Q}(f[S] \setminus f[T]) }{\textbf{H} \;\;\vdash \;\; \textbf{Q}(f[S \setminus T])}](/images/math/3/b/6/3b6a7e21221fc9df829e310d1f8e384b.png) |
where  is WD strict, is WD strict, 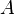 and and 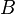 denote types. denote types. |
M
|
| * | DIS_SETMINUS_L |
![\frac{\textbf{H} \;\;\vdash\;\; f^{-1} \in A \pfun B \qquad\textbf{H},\;\textbf{Q}(f[S] \setminus f[T]) \;\;\vdash\;\; \textbf{G}}{\textbf{H},\; \textbf{Q}(f[S \setminus T]) \;\;\vdash \;\; \textbf{G}}](/images/math/e/0/f/e0f8105695bca22877758b8ba283cbec.png) |
where 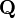 is WD strict, is WD strict, 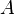 and and 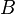 denote types. denote types. |
M
|
| * | SIM_REL_IMAGE_R |
![\frac{\textbf{H} \; \; \vdash \; \; {WD}(\textbf{Q}(\{ f(E)\} )) \qquad\textbf{H} \; \; \vdash \; \; \textbf{Q}(\{ f(E)\} ) }{\textbf{H} \; \; \vdash \; \; \textbf{Q}(f[\{ E\} ])}](/images/math/7/d/f/7dfac56e8c4269e247b888bd790b211d.png) |
M
| |
| * | SIM_REL_IMAGE_L |
![\frac{\textbf{H} \; \; \vdash \; \; {WD}(\textbf{Q}(\{ f(E)\} )) \qquad\textbf{H},\; \textbf{Q}(\{ f(E)\}) \;\;\vdash\;\; \textbf{G}}{\textbf{H},\; \textbf{Q}(f[\{ E\} ]) \;\;\vdash\;\; \textbf{G} }](/images/math/f/6/f/f6fd31552c994d9d3d298f9b5c82d3e9.png) |
M
| |
| * | SIM_FCOMP_R |
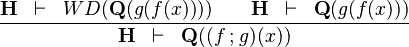 |
M
| |
| * | SIM_FCOMP_L |
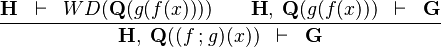 |
M
| |
| * | FIN_SUBSETEQ_R |
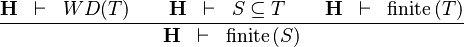 |
the user has to write the set corresponding to 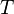 in the editing area of the Proof Control Window in the editing area of the Proof Control Window |
M
|
| * | FIN_BINTER_R |
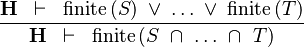 |
M
| |
| * | FIN_SETMINUS_R |
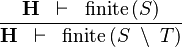 |
M
| |
| * | FIN_REL_R |
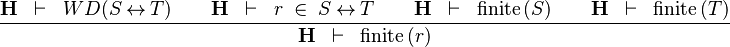 |
the user has to write the set corresponding to 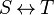 in the editing area of the Proof Control Window in the editing area of the Proof Control Window |
M
|
| * | FIN_REL_IMG_R |
![\frac{\textbf{H} \;\;\vdash \;\; \finite\,(r) }{\textbf{H} \;\;\vdash \;\; \finite\,(r[s])}](/images/math/0/5/1/051dae4a6e35406fa3ee03c69ada792f.png) |
M
| |
| * | FIN_REL_RAN_R |
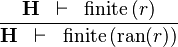 |
M
| |
| * | FIN_REL_DOM_R |
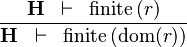 |
M
| |
| * | FIN_FUN1_R |
 |
the user has to write the set corresponding to 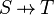 in the editing area of the Proof Control Window in the editing area of the Proof Control Window |
M
|
| * | FIN_FUN2_R |
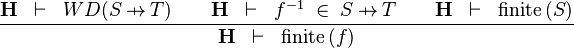 |
the user has to write the set corresponding to 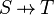 in the editing area of the Proof Control Window in the editing area of the Proof Control Window |
M
|
| * | FIN_FUN_IMG_R |
![\frac{\textbf{H} \;\;\vdash\;\;{WD}(S\pfun T) \qquad\textbf{H} \;\;\vdash \;\; f \;\in\; S \pfun T \qquad \textbf{H} \;\;\vdash \;\; \finite\,(s) }{\textbf{H} \;\;\vdash \;\; \finite\,(f[s])}](/images/math/b/5/8/b5860ef7c2133d3b49f32fa2744c618f.png) |
the user has to write the set corresponding to 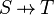 in the editing area of the Proof Control Window in the editing area of the Proof Control Window |
M
|
| * | FIN_FUN_RAN_R |
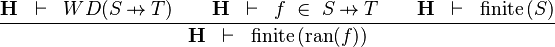 |
the user has to write the set corresponding to 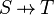 in the editing area of the Proof Control Window in the editing area of the Proof Control Window |
M
|
| * | FIN_FUN_DOM_R |
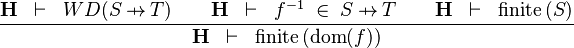 |
the user has to write the set corresponding to 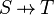 in the editing area of the Proof Control Window in the editing area of the Proof Control Window |
M
|
| * | LOWER_BOUND_L |
 |
 must not contain any bound variable must not contain any bound variable |
M
|
| * | LOWER_BOUND_R |
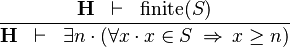 |
 must not contain any bound variable must not contain any bound variable |
M
|
| * | UPPER_BOUND_L |
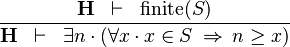 |
 must not contain any bound variable must not contain any bound variable |
M
|
| * | UPPER_BOUND_R |
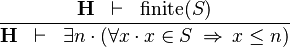 |
 must not contain any bound variable must not contain any bound variable |
M
|
| * | FIN_LT_0 |
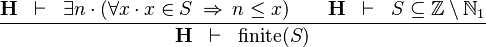 |
M
| |
| * | FIN_GE_0 |
 |
M
| |
CARD_INTERV |
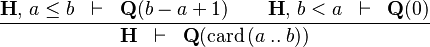 |
where 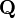 is WD strict is WD strict |
M
| |
CARD_EMPTY_INTERV |
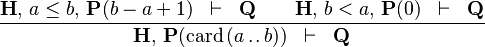 |
where 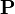 is WD strict is WD strict |
M
| |
| * | DERIV_LE_CARD |
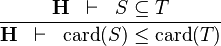 |
 and and 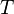 bear the same type bear the same type |
M
|
| * | DERIV_GE_CARD |
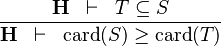 |
 and and 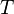 bear the same type bear the same type |
M
|
| * | DERIV_LT_CARD |
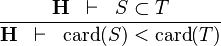 |
 and and 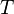 bear the same type bear the same type |
M
|
| * | DERIV_GT_CARD |
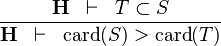 |
 and and 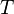 bear the same type bear the same type |
M
|
| * | DERIV_EQUAL_CARD |
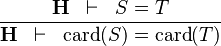 |
 and and 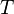 bear the same type bear the same type |
M
|
SIMP_CARD_SETMINUS_L |
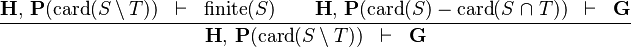 |
where 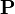 is WD strict is WD strict |
M | |
SIMP_CARD_SETMINUS_R |
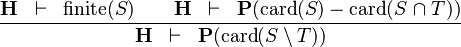 |
where 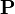 is WD strict is WD strict |
M
| |
SIMP_CARD_CPROD_L |
 |
where 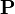 is WD strict is WD strict |
M | |
SIMP_CARD_CPROD_R |
 |
where 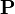 is WD strict is WD strict |
M
| |
| * | FORALL_INST |
![\frac{\textbf{H} \;\;\vdash \;\; {WD}(E) \qquad \textbf{H} , [x \bcmeq E]\textbf{P} \;\;\vdash \;\; \textbf{G}}{\textbf{H}, \forall x \qdot \textbf{P} \;\;\vdash\;\; \textbf{G}}](/images/math/a/c/b/acb596a712a0f720a7d3238f967ccfe6.png) |
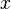 is instantiated with is instantiated with 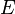 |
M
|
| * | FORALL_INST_MP |
![\frac{\textbf{H} \;\;\vdash \;\; {WD}(E) \qquad \textbf{H}, {WD}(E) \;\;\vdash \;\; [x \bcmeq E]\textbf{P} \qquad \textbf{H}, {WD}(E), [x \bcmeq E]\textbf{Q} \;\;\vdash \;\; \textbf{G}}{\textbf{H}, \forall x \qdot \textbf{P} \limp \textbf{Q} \;\;\vdash\;\; \textbf{G}}](/images/math/e/2/5/e25e646ecaceca4cb4143a3e66dbb185.png) |
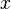 is instantiated with is instantiated with 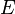 and a Modus Ponens is applied and a Modus Ponens is applied |
M
|
| * | CUT |
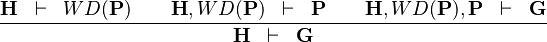 |
hypothesis  is added is added |
M
|
| * | EXISTS_INST |
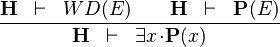 |
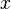 is instantiated with is instantiated with 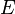 |
M
|
| * | DISTINCT_CASE |
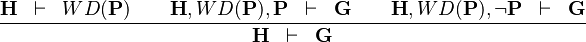 |
case distinction on predicate  |
M
|
| * | ONE_POINT_L |
![\frac{\textbf{H} \;\;\vdash \;\; {WD}(E) \qquad \textbf{H}, \forall x, \ldots, \ldots,z \qdot [y \bcmeq E]\textbf{P} \land \ldots \land \ldots \land [y \bcmeq E]\textbf{Q} \limp [y \bcmeq E]\textbf{R} \;\;\vdash \;\; \textbf{G}}{ \textbf{H}, \forall x, \ldots, y, \ldots, z \qdot \textbf{P} \land \ldots \land y = E \land \ldots \land \textbf{Q} \limp \textbf{R} \;\;\vdash\;\; \textbf{G}}](/images/math/8/b/1/8b19ec24619d8d756596ebe54616be06.png) |
The rule can be applied with 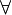 as well as with as well as with 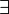 |
A
|
| * | ONE_POINT_R |
![\frac{\textbf{H} \;\;\vdash \;\; {WD}(E) \qquad \textbf{H} \;\;\vdash \;\; \forall x, \ldots, \ldots,z \qdot [y \bcmeq E]\textbf{P} \land \ldots \land \ldots \land [y \bcmeq E]\textbf{Q} \limp [y \bcmeq E]\textbf{R} }{ \textbf{H} \;\;\vdash\;\; \forall x, \ldots, y, \ldots, z \qdot \textbf{P} \land \ldots \land y = E \land \ldots \land \textbf{Q} \limp \textbf{R} }](/images/math/3/7/9/379ac43eaae96f14177427e9cbc89387.png) |
The rule can be applied with 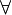 as well as with as well as with 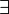 |
A |
See also Extension Proof Rules#Inference Rules.