Empty Set Rewrite Rules
From Event-B
Jump to navigationJump to search
Rules that are marked with a * in the first column are implemented in the latest version of Rodin. Rules without a * are planned to be implemented in future versions. Other conventions used in these tables are described in The_Proving_Perspective_(Rodin_User_Manual)#Rewrite_Rules.
All rewrite rules that match the pattern 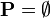 are also applicable to predicates of the form
are also applicable to predicates of the form 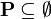 and
and 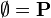 , as these predicates are equivalent. All rewrite rules that match the pattern
, as these predicates are equivalent. All rewrite rules that match the pattern 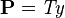 are also applicable to predicates of the form
are also applicable to predicates of the form 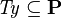 and
and 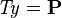 , as these predicates are equivalent.
, as these predicates are equivalent.
| Name | Rule | Side Condition | A/M | |
|---|---|---|---|---|
| * | DEF_SPECIAL_NOT_EQUAL |
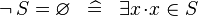 |
where  is not free in is not free in  |
M |
| * | SIMP_SETENUM_EQUAL_EMPTY |
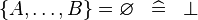 |
A | |
| * | SIMP_SPECIAL_EQUAL_COMPSET |
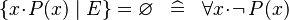 |
A | |
| * | SIMP_BINTER_EQUAL_TYPE |
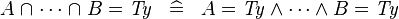 |
where  is a type expression is a type expression |
A |
| * | SIMP_BINTER_SING_EQUAL_EMPTY |
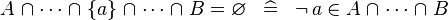 |
A | |
| * | SIMP_BINTER_SETMINUS_EQUAL_EMPTY |
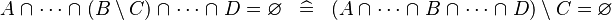 |
A | |
| * | SIMP_BUNION_EQUAL_EMPTY |
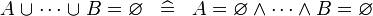 |
A | |
| * | SIMP_SETMINUS_EQUAL_EMPTY |
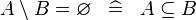 |
A | |
| * | SIMP_SETMINUS_EQUAL_TYPE |
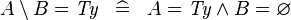 |
where  is a type expression is a type expression |
A |
| * | SIMP_POW_EQUAL_EMPTY |
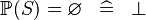 |
A | |
| * | SIMP_POW1_EQUAL_EMPTY |
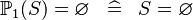 |
A | |
| * | SIMP_KINTER_EQUAL_TYPE |
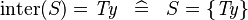 |
where  is a type expression is a type expression |
A |
| * | SIMP_KUNION_EQUAL_EMPTY |
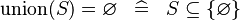 |
A | |
| * | SIMP_QINTER_EQUAL_TYPE |
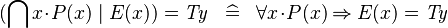 |
where  is a type expression is a type expression |
A |
| * | SIMP_QUNION_EQUAL_EMPTY |
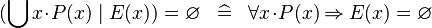 |
A | |
| * | SIMP_NATURAL_EQUAL_EMPTY |
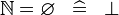 |
A | |
| * | SIMP_NATURAL1_EQUAL_EMPTY |
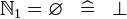 |
A | |
| * | SIMP_TYPE_EQUAL_EMPTY |
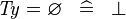 |
where  is a type expression is a type expression |
A |
| * | SIMP_CPROD_EQUAL_EMPTY |
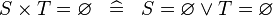 |
A | |
| * | SIMP_CPROD_EQUAL_TYPE |
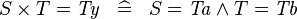 |
where  is a type expression equal to is a type expression equal to 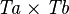 |
A |
| * | SIMP_UPTO_EQUAL_EMPTY |
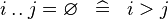 |
A | |
| * | SIMP_UPTO_EQUAL_INTEGER |
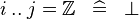 |
A | |
| * | SIMP_UPTO_EQUAL_NATURAL |
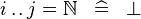 |
A | |
| * | SIMP_UPTO_EQUAL_NATURAL1 |
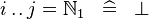 |
A | |
| * | SIMP_SPECIAL_EQUAL_REL |
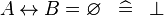 |
idem for operators 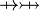 |
A |
SIMP_TYPE_EQUAL_REL |
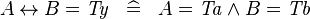 |
where  is a type expression equal to is a type expression equal to 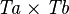 |
A | |
| * | SIMP_SPECIAL_EQUAL_RELDOM |
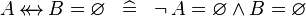 |
idem for operator 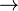 |
A |
SIMP_TYPE_EQUAL_RELDOMRAN |
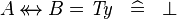 |
where  is a type expression, idem for operator is a type expression, idem for operator 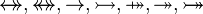 |
A | |
| * | SIMP_SREL_EQUAL_EMPTY |
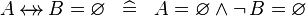 |
A | |
| * | SIMP_STREL_EQUAL_EMPTY |
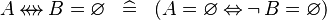 |
A | |
| * | SIMP_DOM_EQUAL_EMPTY |
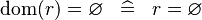 |
A | |
| * | SIMP_RAN_EQUAL_EMPTY |
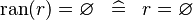 |
A | |
| * | SIMP_FCOMP_EQUAL_EMPTY |
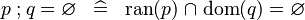 |
A | |
| * | SIMP_BCOMP_EQUAL_EMPTY |
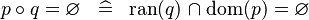 |
A | |
| * | SIMP_DOMRES_EQUAL_EMPTY |
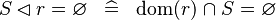 |
A | |
| * | SIMP_DOMRES_EQUAL_TYPE |
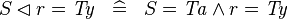 |
where  is a type expression equal to is a type expression equal to 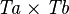 |
A |
| * | SIMP_DOMSUB_EQUAL_EMPTY |
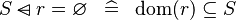 |
A | |
| * | SIMP_DOMSUB_EQUAL_TYPE |
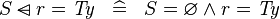 |
where  is a type expression is a type expression |
A |
| * | SIMP_RANRES_EQUAL_EMPTY |
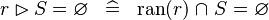 |
A | |
| * | SIMP_RANRES_EQUAL_TYPE |
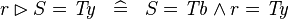 |
where  is a type expression equal to is a type expression equal to 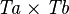 |
A |
| * | SIMP_RANSUB_EQUAL_EMPTY |
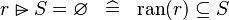 |
A | |
| * | SIMP_RANSUB_EQUAL_TYPE |
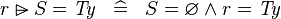 |
where  is a type expression is a type expression |
A |
| * | SIMP_CONVERSE_EQUAL_EMPTY |
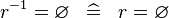 |
A | |
| * | SIMP_CONVERSE_EQUAL_TYPE |
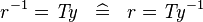 |
where  is a type expression is a type expression |
A |
| * | SIMP_RELIMAGE_EQUAL_EMPTY |
![r[S] = \emptyset \;\;\defi\;\; S \domres r = \emptyset](/images/math/3/8/f/38f444db2941b8e696a89faeec9b7623.png) |
A | |
| * | SIMP_OVERL_EQUAL_EMPTY |
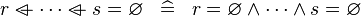 |
A | |
| * | SIMP_DPROD_EQUAL_EMPTY |
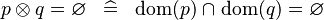 |
A | |
| * | SIMP_DPROD_EQUAL_TYPE |
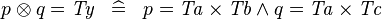 |
where  is a type expression equal to is a type expression equal to 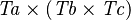 |
A |
| * | SIMP_PPROD_EQUAL_EMPTY |
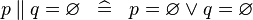 |
A | |
| * | SIMP_PPROD_EQUAL_TYPE |
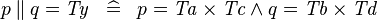 |
where  is a type expression equal to is a type expression equal to 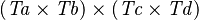 |
A |
| * | SIMP_ID_EQUAL_EMPTY |
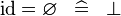 |
A | |
| * | SIMP_PRJ1_EQUAL_EMPTY |
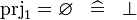 |
A | |
| * | SIMP_PRJ2_EQUAL_EMPTY |
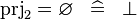 |
A |