Identifier Decomposition
Purpose
When translating from set theory to pure predicate calculus, it is necessary that there is no identifier of a Cartesian product type, because their presence would block the translation. We therefore need a service for decomposing such identifiers into fresh ones that have a simpler type.
For instance, consider the predicate
it contains two identifiers which are both of type 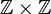 which is a Cartesian product. We therefore would like to transform it into the equivalent predicate
which is a Cartesian product. We therefore would like to transform it into the equivalent predicate
where all identifiers have a simple type, namely 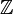 .
.
This transformation is already performed by the method
ISimpleSequent org.eventb.pptrans.Translator.decomposeIdentifiers(ISimpleSequent)
but its implementation is a bit clumsy, especially as concerns bound identifiers.
Specification
The specification of this transformation is quite simple: We want a transformer that decomposes all identifiers, both free and bound, into simpler ones, without altering the semantics of the predicates. This transformation shall be applied globally to a simple sequent, so that all free identifiers are decomposed in the same manner.
This transformation shall be available as a service provided by the Sequent Prover plug-in.
Implementation
Decomposing free identifiers is easily done as the type environment of the simple sequent is known. Just harvest the type environment for free identifiers of Cartesian product type and replace them with fresh identifiers of simpler type. All the necessary bricks are already available from the AST library.
Decomposing bound identifiers is a bit more difficult, because decomposition introduces new bound identifiers and one has to update the de Bruijn indexes. It is our experience that this is error prone. So the implementation shall rely on already available primitives from the AST library, rather than trying to reimplement them, even at the cost of somewhat degraded efficiency.
The way to proceed is to rewrite in turn each quantified expression and predicate that needs to (i.e., that contains a declaration of Cartesian product type). The rewrite is to be performed in this manner
- Create new declarations based on existing ones, where declarations of Cartesian product type have been decomposed.
- Insert these declarations above the quantified node to rewrite and instantiate the quantified node with the corresponding bound identifiers.
On the example above, we therefore build the intermediate formula
which gives the expected result once the substitution has been applied.
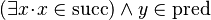
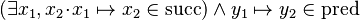
![\exists x_1, x_2\qdot [x := x_1\mapsto x_2] (x\in\textrm{succ})](/images/math/5/e/8/5e8335140da2038a6e444aa7930eb148.png)