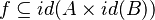Mathematical Language Evolution Design
Introduction
This document describes the modifications that occur to the Event-B mathematical language from the developer point of view. The old language will still be recognized, in order to provide backward compatibility.
These changes are described from a user point of view in Changes to the Mathematical Language of Event-B.
Abstract Syntax Tree
Deprecated nodes (becoming atomic expressions):
- KPRJ1
- KPRJ2
- KID
New nodes:
- KPARTITION that represents the new partition predicate (multiple predicate)
- KPRJ1_GEN that represents the generic atomic version of the first projection
- KPRJ2_GEN that represents the generic atomic version of the second projection
- KID_GEN that represents the generic atomic version of the identity
Parser Changes
The new parser has a version attribute. Depending on the version, formulas are parsed differently. Thus, the KPARTITION node is a regular identifier if version is V1. It is accepted as a keyword only from version V2. Concerning identity and projections, they are recognized as non-generic with V1 and generic with V2. The following table summarizes how tokens are processed depending on the language version:
| Language V1 | Language V2 | |
|---|---|---|
| "partition" | IDENT | KPARTITION |
| "id" | KID | KID_GEN |
| "prj1" | KPRJ1 | KPRJ1_GEN |
| "prj2" | KPRJ2 | KPRJ2_GEN |
Parsing
FormulaFactory has new parse() methods with a language version argument. Existing methods default to the first version (LanguageVersion.V1), while becoming deprecated. Thus, one now has to know, before parsing a formula, the version of the language it has been written with. It also provides methods to upgrade to the new language version.
Multiple Predicates / Partition
A new predicate class is introduced: MultiplePredicate, in which the partition predicate is implemented. A MultiplePredicate is a predicate that applies to a list of one or more expressions. In a partition, all expressions must have the same type, that is the type of the partitioned set (first child).
Associativity
Newly non associative relational set operators now require parentheses around their operands for parsing to succeed. This is managed directly by the parser. Unparsing also requires those parentheses, so the BinaryExpression.toString() method has been changed accordingly.
Visitors
Partition, identity and projections also entail new visitor methods, as follows:
IVisitor has 6 more methods:
- enterKPARTITION(MultiplePredicate)
- continueKPARTITION(MultiplePredicate)
- exitKPARTITION(MultiplePredicate)
- visitKID_GEN(AtomicExpression)
- visitKPRJ1_GEN(AtomicExpression)
- visitKPRJ2_GEN(AtomicExpression)
ISimpleVisitor has 1 more method:
- visitMultiplePredicate(MultiplePredicate)
Thus, implementors of those interfaces are required to implemented new methods, while subclassers of DefaultVisitor and DefaultSimpleVisitor should consider whether or not to override them.
Upgrade
Formulas written with version V1 will need upgrading to version V2. However, many V1 formulas will be exactly the same in V2. A formula needs ugrading if:
- it contains one of {KPRJ1, KPRJ2, KID}
- it contains a non parenthesised sequence of relational set operators
- it contains an identifier named "partition" (that would conflict with the new predicate of the same name)
In these cases an upgrade procedure has to be applied to the formula, in order to make it parseable with V2 mathematical language. It consists in rewriting KPRJ1, KPRJ2, KID expressions into their generic equivalent (see Changes to the Mathematical Language of Event-B#Generic Identity and Projections). For parentheses, the difference is only visible in a string representation, where the missing ones are added by the toString() method. Bound identifiers named "partition" are renamed "partition1".
Upgraded formulas can be obtained from a formula string by calling one of the new FormulaFactory.upgrade() methods. This will return a IUpgradeResult as described below.
Please notice that the version of a formula is not known by the Formula object itself. Instead, one has to know, before parsing or upgrading a formula string, which version of the mathematical language is has been written with. If the string is extracted from a RodinFile, it may be guessed from the file version (see #File upgrade).
Upgrade result
FormulaFactory.upgrade() methods return a IUpgradeResult that can be queried for:
- whether or not the upgrade is a success
- problems that occurred while attempting the upgrade
- the upgraded formula, if upgrade succeeded
File upgrade
Existing rodin files with V1 formulas inside need converting to V2 formulas. Concerned files are:
- Contexts
- Machines
- Proofs
This is managed through the version tools of the rodin core package: a new version number for each of these files represents the passing from V1 to V2 mathematical language. The following table summarizes the correspondence between file version number and mathematical version number:
| Math V1 | Math V2 | |
|---|---|---|
| Context | 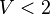
|
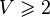
|
| Machine | 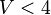
|
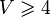
|
| Proof | 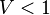
|
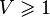
|
In those XML files, the formulas are written inside various attributes. Existing version conversion tools (in
) allowed making changes to the structure of the files (adding an element, renaming an attribute, …), through XSL transformations, targetting a single element to apply the conversion to.
But upgrading formulas entails dealing with the contents of attributes in various elements dispatched all over the file. So, extending the conversion tools, a new conversion operation is implemented (ModifyAttribute) that changes the contents of an attribute, together with a new kind of file conversion: 'multiple' conversion, in contrast to 'simple' conversion. This new one allows targetting several elements through unrestricted XPath expressions.
These new core tools extend the existing 'conversions' extension point. It now allows writing conversion extensions in
client package that target every assignment, expression or predicate in any context, machine or proof file and upgrade their contents to the new language version.
The modifying code is delegated to the client that must provide, in the conversion extension, a class that implements IAttributeModifier. It builds the new string value of the attribute from the value read in the file. In our case, it builds a V2 formula that is the upgraded equivalent to the given V1 formula.
Formula upgrade
Formatting
Ideally, upgrading a formula would preserve its previous formatting (spaces, tabs, new lines). But this turns out being quite tricky. Indeed, it prevents from simply rewriting the formula then applying a toString(), as this would totally forget and override any formatting. Thus, we would have to write directly into the original string. Firstly find the source locations where changes will occur, then patching the formula with the new expression versions at those source locations.
But that leads to more complexity when we come to consider formulas that contain
- recursive relational set operators (that recursively shift source locations)
- binary operators with higher priorities nearby (that mindlessly absorb a member of the rewritten expression)
Let's look at the following formula:
A straight rewriting would proceed as follows:
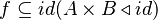 which already is false (requires parentheses)
which already is false (requires parentheses)
Then, with the appropriate shift of the source location to replace the first 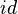 operator:
operator:
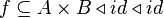 which is even worse
which is even worse
This suggests putting parentheses around rewritten expressions. But they would sometimes be superfluous, which brings us to distinguish cases where they are needed and cases where they are not, depending on the priority of the operators nearby.
Considering this is going quite far, a simpler upgrade method is applied:
- if the formula does not use deprecated expressions, nor lacks parentheses around relational set operators, it is left unchanged, preserving the formatting
- it it does, it is rewritten and any previous formatting is overridden
Detecting missing parentheses
Missing parentheses can be quite easily detected, given a parsed formula and its string.
Using a visitor, we check each relational set expression.
Starting from its source location, we search the string for parentheses towards both left and right directions around the expression, skipping space characters. If the first non space character is not the expected parenthesis, then one is missing and the formula needs upgrading to V2.
The fussy part is about the definition of space characters.
c is an Event-B white space character if one of the following holds: * java.lang.Character.isSpaceChar(c) * '\u0009' <= c && c <= '\u000d' * '\u001c' <= c && c <= '\u001f'
A new isEventBWhiteSpace(char) method has been provided in FormulaFactory to prevent developers from worrying about the details of this matter.
Typing generic operators
The problem of typing generic operators arises when upgrading a fomula like 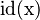 .
We know that, in the general case, the upgraded version is
.
We know that, in the general case, the upgraded version is 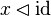 .
But which type should the generic
.
But which type should the generic 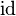 bear ?
bear ?
An answer is:
If the V1 operator is typed, then the V2 generic one should bear the same type.
Given the convention that 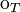 means that
means that 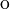 has type
has type 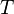 , this entails rewriting
, this entails rewriting 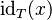 into
into 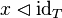 .
.
But then, what happens if 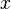 is a type expression,like
is a type expression,like 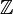 ?
?
We would come to rewriting 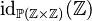 into
into 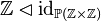 .
.
In this case, the domain restriction is clearly superfluous. This brings in a new rule:
If the V1 unary operator has a type expression for argument, then the V2 generic atomic one needs no domain restriction
Putting things together, the following table summarizes the upgrade of generic operators, based on the 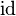 operator example. Similar rules apply to
operator example. Similar rules apply to 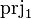 and
and 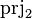 .
.
| Math V1 | Math V2 | |
|---|---|---|
| Type expression | 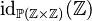
|
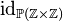
|
| Typed | 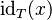
|
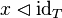
|
| Not typed | 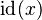
|
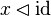
|
Identifiers named "partition"
Identifiers named "partition" will conflict with the new "partition" predicate if the formula does not rename them. But we cannot always rename an identifier in a formula without breaking things outside.
Thus, free identifiers will not be renamed. This is a not upgradable case.
Concerning bound identifiers, we simply have to rename them as "partition1". The toString() method deals with alpha conversion if a bound identifier "partition1" already exists.
Not upgradable cases
In some situations, an upgrade would be needed (the formula contains 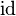 ,
, 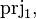
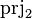 , a "partition" bound identifier or lacks parentheses) but it is simply not possible to achieve it.
Those cases are:
, a "partition" bound identifier or lacks parentheses) but it is simply not possible to achieve it.
Those cases are:
- the formula string does not parse
- the formula contains a "partition" free identifier
In the upgrade result, that will appear as a problem of kind ProblemKind.notUpgradableError.
Changes to client code
Client code based on the "Formula.tom" file provided in the AST package can now use the "FormulaV2.tom" file instead to take the syntax modifications into account. However, the former file is left unchanged to allow clients to keep on using it and decide whether and when to upgrade their code to V2.
In the sequent prover, the tactic that used to rewrite
E ↦ F ∈ id(S) into E ∈ S ∧ F = E
now rewrites
E ↦ F ∈ id into E = F
In PP Translator, rules that concern 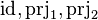 are changed so that they take generic operators as input (see ppTrans documentation, rules IR39, IR43, IR44).
are changed so that they take generic operators as input (see ppTrans documentation, rules IR39, IR43, IR44).
Expanders
The new Partition predicate needed to be processed by the translator and the sequent prover, performing essentially the same job: to rewrite a partition predicate into its definition. To that purpose, a common framework of Expanders was implemented. Expanders aim at rewriting ("expanding") the definitions of some mathematical operators. For the time being, only a partition expander exists, but others may follow.
Thus, a new rule was implemented to translate partition into its definition (see ppTrans documentation, rule BR8).
In the prover, a tactic "org.eventb.core.seqprover.partitionRewriteTac" is added as part of the default auto-tactics. It can also be applied manually in the prover ui by clicking a "partition" in a formula.