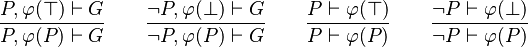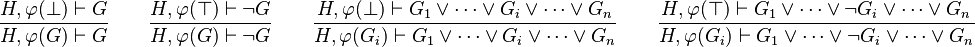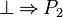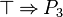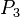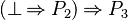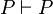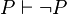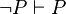Modus Ponens generalized
This page describes the design of a tactic replacing a predicate 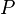 in either a hypothesis or a goal by
in either a hypothesis or a goal by 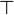 (respectively
(respectively 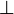 ) if
) if 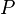 (respectively
(respectively 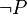 ) is a hypothesis. That tactic is slightly different from the one requested : Feature Request #3137918
) is a hypothesis. That tactic is slightly different from the one requested : Feature Request #3137918
Objective
A sequent can be simplified by finding every occurrence of a hypothesis in the other hypotheses or goal, and replacing it by 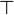 or
or 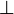 as explained below:
as explained below:
Moreover, owing to this equivalence 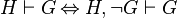 we can infer four others rules :
we can infer four others rules :
Contrarily to the Feature Request, the rule is applied on every occurrence of 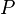 and not only on the one appearing in a disjunctive form. Also, to prevent spending to much time analyzing a sequent, only goal and visible hypotheses can be re-written, using every hypothesis (global and local). The analysis performance of a sequent can be problematic since every predicate of goal and visible hypotheses are checked. But it is still worthy because it may simplify a lot, and so make proof obligations simpler and more legible to users.
and not only on the one appearing in a disjunctive form. Also, to prevent spending to much time analyzing a sequent, only goal and visible hypotheses can be re-written, using every hypothesis (global and local). The analysis performance of a sequent can be problematic since every predicate of goal and visible hypotheses are checked. But it is still worthy because it may simplify a lot, and so make proof obligations simpler and more legible to users.
Legacy
There already exists a reasoner that performs part of this tactic : autoImpF (ImpE automatic). It looks for implicative hypothesis in a sequent. Among the predicates computed by breaking possible conjunctions in the left-hand side of the implication, it checks if some appear in selected hypothesis. In that case, every predicate which is also a hypothesis (global or local) is removed from the left-hand side of the implication. If no predicate remains, then the right-hand side of the implication is re-written as a list of conjunction, else implication is re-written without the removed predicates (possibly none).
Then this reasoner can be considered as "intelligent" because it finds itself the positions where to apply, which entails a code hard to read. However, as reasoners are in the trusted base, they should be easily understandable.
Design Decision
The main drawback of this tactic is its execution time. Indeed, each (actually it is not the case but it helps to see how greedy this tactics can be) sub-predicate of each goal and visible (or selected) hypothesis is compared to the other hypotheses (global and local). Several strategies can be applied in order to reduce that execution-time :
- When a predicate match a hypothesis, its children need not be analyzed.
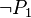
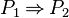
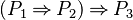
- In this example, the sub-predicate
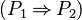 of the third predicate matches the second one. It is replaced by
of the third predicate matches the second one. It is replaced by  , and all its children must not to be analyzed (even if
, and all its children must not to be analyzed (even if 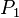 could have been replaced by
could have been replaced by 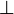 because of the first predicate).
because of the first predicate).
- Each hypothesis must be scanned only once to avoid accumulating predicate's running time. From that point of view, two decisions can be inferred :
- A given predicate is compared once to every hypothesis. For instance, we do not try to find every occurrence of a hypothesis among the goal and the visible (or selected) hypothesis. In that case, each predicate would be scanned many times, accumulating execution time.
- That tactic apply the rules specified here-above everywhere it is possible. Thus, from this set of hypothesis :
- We will reach immediatly :
- Which will be re-written to :
- Instead of writing :
- Re-written :
- And then :
- Re-written :
- In the case of n-ary predicates, each possibility is not tested.
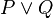
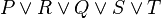
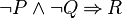
- In this example,
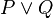 could be replaced by
could be replaced by 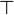 in the second predicate. In order not to add more computing time, this kind of replacement is not computed.
in the second predicate. In order not to add more computing time, this kind of replacement is not computed.
- When a predicate is both a hypothesis and a goal (or contained in a disjunctive goal), then, re-writing are uppermost proceeded using the hypothesis.
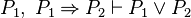
- is re-written as :
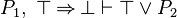
- instead of :
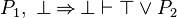
- Goal's predicates should not be re-written using the goal istelf.
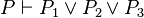 should not be re-written
should not be re-written 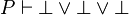 since it surely lead us in a deadlock in most cases.
since it surely lead us in a deadlock in most cases.
This reasoner can be considered as "intelligent," similarly to autoImpF because it computes by its own where it has to apply the rules.
Implementation
In this part is explained how the previous choices have been implemented with Java.
- First, every hypothesis of the sequent is stocked in a Set called hypSet. If the hypothesis is a negation (e.g.
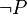 ) then its child (
) then its child (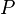 ) is actually the predicate stored in the set. Currently, if a hypothesis is in the form
) is actually the predicate stored in the set. Currently, if a hypothesis is in the form 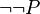 , then
, then 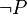 is stored. It is due to the fact that for every predicate stored in that set, we check if it or its negation is actually a hypothesis (before the re-writing to ensure we are not doing wrong works). Indeed, let's imagine that there is a hypothesis in the form
is stored. It is due to the fact that for every predicate stored in that set, we check if it or its negation is actually a hypothesis (before the re-writing to ensure we are not doing wrong works). Indeed, let's imagine that there is a hypothesis in the form 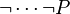 . By storing its child, it easy to find that it or its negation is actually a hypothesis. But, by storing
. By storing its child, it easy to find that it or its negation is actually a hypothesis. But, by storing 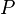 , it is hard to find the initial hypothesis as the number of
, it is hard to find the initial hypothesis as the number of  can't be known in advance.
can't be known in advance.
In addition, predicate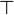 or
or 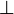 are not stored in the set. First, because it is fool to re-write such predicate. Moreover we can create infinite loop (drop of performance and the job performed is not worth). Indeed, let's imagine that we have the following sequent :
are not stored in the set. First, because it is fool to re-write such predicate. Moreover we can create infinite loop (drop of performance and the job performed is not worth). Indeed, let's imagine that we have the following sequent : 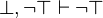 . Here is how the tactic will re-write it :
. Here is how the tactic will re-write it :
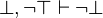
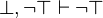
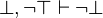
- etc.
- Secondly, the goal is stocked in a set called goalToHypSet. As previously, if it denotes a negation, then its child is stocked. Moreover, if it denotes a disjunction, then every member is stocked, or their child, if they denote a negation.
-
- Then the goal is analyzed, i.e. each sub-predicate is compared to the predicates contained in hypSet (the set of hypotheses). If it matches, the predicate is stored in a Map (modifGoalMap) as well as its position, else its children are analyzed in the same way. Finally, the Map contains the sub-predicates which will be re-written (Map's key) mapped to the list of position where they will be replaced. Notice that the goal itself can be contained in the the Map modifGoalMap.
- Visible hypotheses are analyzed like the goal, except that we use hypSet and goalToHypSet. To not compare to itself, it (or its child in case of a negation) is removed of the set hypSet. If the hypothesis can be re-written, then it is stored in a map whose the key is the hypothesis itself, and the value is the same as the Map describes for the goal. After analyzing, the hypothesis (or its child in case of a negation) is re-added to the set hypSet.
-
- Afterwards, goal is re-written using rewriteSubFormula given in Predicate. For each predicate in the Map modifGoalMap, we check if it is (respectively its negation) actually a hypothesis of the sequent. If so, we ensure that it is equal to the predicate situated at the given position. Finally, if so, we replace it by
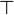 (repsectively
(repsectively 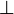 ). Then, we catch the re-written goal and the hypotheses needed to achieve it.
). Then, we catch the re-written goal and the hypotheses needed to achieve it. - We proceed the same for hypothesis of the map modifHypMap. At the end, all IHypAction are stored in a List.
- Afterwards, goal is re-written using rewriteSubFormula given in Predicate. For each predicate in the Map modifGoalMap, we check if it is (respectively its negation) actually a hypothesis of the sequent. If so, we ensure that it is equal to the predicate situated at the given position. Finally, if so, we replace it by
- Finally, the proof rule is made. There are 5 cases :
- the goal is re-written but not the hypotheses : an antecedent is created with no IHypAction, and the IProofRule is made with the needed hypotheses.
- the goal and hypotheses are re-written : an antecedent is created with the IHypAction computed, and the IProofRule is made with the needed hypotheses.
- hypotheses are re-written but not the goal : the IProofRule is made with the IHypAction computed.
- hypotheses are re-written but not the goal, but the goal is used to re-write hypotheses : an antecedent is created with the IHypAction computed (the new goal is the current goal), and the IProofRule is made with the needed hypotheses.
- nothing has been re-written : the tactic is no more applicable.
Currently, that implementation has few drawbacks.
- Those followings sequents are not re-written (that tactic should be coupled with GoalInHypTac and findContrHypsTac) :
- Its time execution is enormous because of the work that tactic performed (intrinsic), and because of the test realized to ensure that all re-writing recorded in the maps are correct.
Complement
In Rodin 3.0, this reasoner has been improved by integrating Variations in HYP, CNTR and GenMP.