New Proof Rules
This document describes the set of newly added reasoners for improving the usability of the prover within Rodin Platform. The work has been done originally by Stephan Merkli, Michael Schaufelberger and David Simmen as their project for an object oriented programming course at ETH Zürich. The aim of the work is to try out the extensibility feature of the RODIN platform related to the prover. The rules are added using as various plug-ins with most of the work done in a declarative fashion. Moreover the new features are also tested using the pre-defined framework which has been set-up during the development of the RODIN platform. The rules are of different types: automatic/interactive rewriting or more general inference rules.
Remove Membership for Range
The work is related to the following rewriting rule:
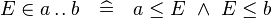
The rule has been implemented so that it can be applied both automatically and interactively.
- Automatically: The rule can be chosen from the Preferences of the Sequent Prover to be run as a part of the Automatic Prover or as a part of the Post-Tactic. The rewriting is carried out to all sub-formulas of the form
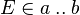 .
.
- Interactively: The
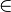 symbol is redden in the formular (either goal or hypotheses) and is applied only to the sub-formula as indicated by the user.
symbol is redden in the formular (either goal or hypotheses) and is applied only to the sub-formula as indicated by the user.
Automatic Rule for Overriding
The work is related to the following rewriting rule:
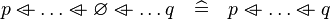
(i.e. removing 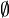 for overriding
for overriding 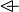 operator)
operator)
The rule is added so that it can be applied automatically. User can choose the rule from the Preferences of the Sequent Prover, so that it can be run as a part of the Automatic Prover or as a part of the Post-Tactic. The rewriting is carried out to all sub-formulas of the form that match the left-hand side of the rule.
Automatically Apply De Morgan's Laws
The work is related to the following rewriting rules (De Morgan's Laws):
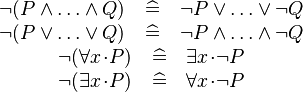
Currently, these rewriting rules can be invoked manualy during interactive proofs. The rules is added so that user can choose from the Preferences of the Sequent Prover, so that they can be run as a part of the Automatic Prover or as a part of the Post-Tactic. The rewriting is recursively carried out to all sub-formulas of the form that match the left-hand side of the one of the rule.
Automatically Rewrite 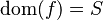
The work is about rewriting automatically 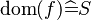 for selected hypotheses and goal if there is a hypothesis that
for selected hypotheses and goal if there is a hypothesis that 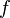 is a total function from
is a total function from  , e.g.
, e.g.
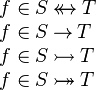
The rule is added so that it can be applied automatically. User can choose the rule from the Preferences of the Sequent Prover, so that it can be run as a part of the Automatic Prover or as a part of the Post-Tactic.
Interactively Rewrite 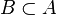
The work is about providing support for interactively proving 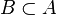 according to the following rewriting rules.
according to the following rewriting rules.
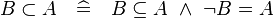
The rule has been implemented so that it can be applied both automatically and interactively.
- Automatically: The rule can be chosen from the Preferences of the Sequent Prover to be run as a part of the Automatic Prover or as a part of the Post-Tactic. The rewriting is carried out to all sub-formulas of the form
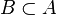 .
.
- Interactively: The
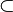 symbol is redden in the formula (either goal or hypotheses) and is applied only to the sub-formula as indicated by the user.
symbol is redden in the formula (either goal or hypotheses) and is applied only to the sub-formula as indicated by the user.