Revisiting Feasibility POs

The Issue

Son recently reported a bug in the Proof Obligation Generator (POG) of Rodin 2.3 where one could have an event-B project containing two machines where all proof obligations are discharged automatically although the concrete machine contains invariant 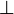$\bfalse$. This is not something expected so some proof obligations must be wrong.

Analysis

Looking more closely at the example attached to the bug, it appears that the initialisation of the concrete machine is magic. It is therefore normal that it can establish a 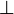$\bfalse$ invariant. However, the feasibility proof obligation FIS is supposed to work as a filter and prevent models from containing magic actions. In the example, the FIS proof obligation of the concrete initialisation is easily discharged and thus does not play its filter role. This proof obligation is therefore wrong and needs to be fixed.

In a nutshell, the example attached to the bug, can be reduced to the following. Take a machine M with the following contents

 MACHINE
 	M
 VARIABLES
 	v
 INVARIANTS
 	inv1:	v = 1	  not theorem
 EVENTS
 	INITIALISATION:	  not extended ordinary
 		THEN
 			act1:	v :∣ v' = 1
 		END
 END

and a concrete machine N refining M such as

 MACHINE
 	N
 REFINES
 	M	
 VARIABLES
 	w
 INVARIANTS
 	inv1:	v = −(w * w)	  not theorem
 EVENTS
 	INITIALISATION:	  not extended ordinary
 		WITH
 			v':	v' = −(w' * w')
 		THEN
 			act1:	w :∣ w' * w' = −1
 		END
 END

In Rodin 2.3, the FIS PO generated for the action of the initialisation of N is

    −(w' * w') = 1
 |- ∃ w' · w' * w' = −1

which is a contraction of the theoretical proof obligation

     v' = 1                  // abstract before-after predicate
     v' = −(w' * w')         // witness
 |-  ∃ w' · w' * w' = −1     // feasibility predicate

where the witness (which is deterministic) has been applied as a substitution to the abstract before-after predicate.

This proof obligation is easily discharged by instantiating the existential quantifier of the goal with 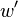$w'$.

From this example, the flaw in the proof obligation comes from the presence of the two hypotheses together. If we remove any of them, then the proof obligation becomes unprovable, as expected. So, we need to remove at least one of these hypotheses to make the FIS PO correct.

A Bit of History

In Jean-Raymond Abrial's book, the feasibility PO does not contain any of these hypotheses. It was also the case in early versions of the Rodin platform. Looking at the code history, it appears that the faulty hypotheses were added in commit r2786 of Tue Jan 9 2007 with comment

Changed structure of generated POs.
The POG now tries to put feasibility of abstract actions in the hypothesis of refined event actions. As a consequence the guard strengthening PO is now stronger.

The idea backing this change was to try to allow users to reuse somehow the feasibility proof already carried on for the abstract actions when proving feasibility of the concrete actions. For this, the POG adds one hypothesis which corresponds to the feasibility predicate already proved in the abstraction together with the witness that describes the link between the abstract and concrete actions.

However, stating the witness that links after values of abstract and concrete variables introduces a circular argument, as the witness existence supposes that after values of concrete variables do exist (this is the WFIS proof obligation), which is the exact meaning of the feasibility proof obligation. We thus have a proof obligation to demonstrate the existence of something, assuming that this something already exists!

Similarly, the feasibility of abstract actions has been proved under the guards of the abstract event. These abstract guards are themselves proved to be a logical consequence of the concrete guards (GRD or MRG proof obligations). However, this latter proof also includes witnesses in hypotheses. We therefore have the same circular argument appearing again.

In summary, it appears that, in the general case, both the abstract before-after predicate and the witness must not put in hypothesis of any concrete feasibility proof obligation.

Possible Solutions

Introducing the abstract feasibility predicate in hypothesis seemed to be a good idea. But it is currently unsound. How could we change the proof obligation generation to reintroduce this predicate without introducing unsoundness?

The issue at stake is the circular argument about the existence of the witness. However, there are actually two kinds of witnesses: witnesses for abstract parameters and witnesses for after values of abstract variables. The parameter witness is actually the only one needed when proving guard strengthening. So, if we restrict this witness to not contain any occurrence of a concrete after value, then we break the circle. The existence of the parameter witness does not depend any more on the concrete before-after predicate of the concrete event.

Then, we can also constrain the guard strengthening proof obligations (GRD and MRG proof obligations) to only contain parameter witnesses in hypothesis (this is the approach retained in Abrial's book). This would then allow us to introduce the abstract guards and then the abstract before-after predicate as hypotheses of the concrete feasibility proof obligation.

This is actually what is implemented in the proof obligation generator of Rodin 2.3. So, it is valid in this release to introduce the abstract before-after predicate, as far as no parameter witness contains any after-value.

As concerns the witness for after values of abstract variables, we can get the following insight: the purpose of this witness is to describe how one can compute abstract after values from concrete ones. It is the purpose of the WFIS proof obligation to demonstrate that this computation is actually feasible.

However, in the case of the feasibility proof obligation, we need to go in the opposite direction: we know that we have abstract after values and we want to show the existence of concrete ones. We therefore want to use the witness in the opposite direction. And no proof obligation is generated to show that the witness can indeed be used in this opposite direction.

So, we have two possibilies for fixing the feasibility proof obligation with respect to this witness:

1. Either we keep the witness as hypothesis, but we generate a new proof obligation to show that the witness can be used to compute concrete after values from abstract ones.
2. or we get rid of the witness in the feasibility proof obligation.

The first solution looks a bit heavy, as feasibility is the only place where the witness is used in the direction from abstract to concrete. In all other proof obligations, it is used from concrete to abstract. Therefore, introducing a new proof obligation just for this is not worth it.

In the second solution, during proof, one can always state again the witness, prove that it is invertible and then use it to achieve the proof. So leaving out the witness does not loose any expressivity and is indeed much simpler.

Similar Proof Obligation

Looking at the code of the proof obligation generator, it appears that the well-definedness (WD) proof obligation for concrete actions also has both the abstract before-after predicate and the witness in hypothesis. So this proof obligation is also erroneous as we've seen that this combination of hypothesis can introduce inconsistency. Following the same reasoning, it is decided to also drop the witness from WD proof obligations.

Conclusion

In summary, both the abstract before-after predicate and the witness hypothesis must be dropped from both the well-definedness and feasibility proof obligations of concrete actions. However, if no parameter witness contains any after value, it is possible to introduce the abstract before-after predicate in hypothesis.