All Rewrite Rules
CAUTION! Any modification to this page shall be announced on the User mailing list!
This page groups together all the rewrite rules implemented (or planned for implementation) in the Rodin prover. The rules themselves can be found in their respective location (for editing purposes):
Conventions used in these tables are described in The_Proving_Perspective_(Rodin_User_Manual)#Rewrite_rules
Set Rewrite Rules
Rules that are marked with a * in the first column are implemented in the latest version of Rodin. Rules without a * are planned to be implemented in future versions. Other conventions used in these tables are described in The_Proving_Perspective_(Rodin_User_Manual)#Rewrite_Rules.
| Name | Rule | Side Condition | A/M | |
|---|---|---|---|---|
| * | SIMP_SPECIAL_AND_BTRUE |
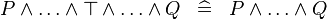 |
A | |
| * | SIMP_SPECIAL_AND_BFALSE |
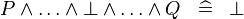 |
A | |
| * | SIMP_MULTI_AND |
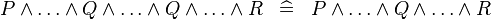 |
A | |
| * | SIMP_MULTI_AND_NOT |
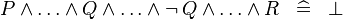 |
A | |
| * | SIMP_SPECIAL_OR_BTRUE |
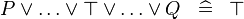 |
A | |
| * | SIMP_SPECIAL_OR_BFALSE |
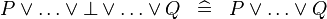 |
A | |
| * | SIMP_MULTI_OR |
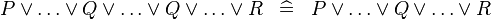 |
A | |
| * | SIMP_MULTI_OR_NOT |
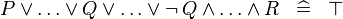 |
A | |
| * | SIMP_SPECIAL_IMP_BTRUE_R |
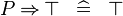 |
A | |
| * | SIMP_SPECIAL_IMP_BTRUE_L |
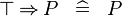 |
A | |
| * | SIMP_SPECIAL_IMP_BFALSE_R |
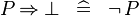 |
A | |
| * | SIMP_SPECIAL_IMP_BFALSE_L |
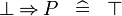 |
A | |
| * | SIMP_MULTI_IMP |
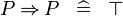 |
A | |
| * | SIMP_MULTI_IMP_NOT_L |
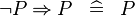 |
A | |
| * | SIMP_MULTI_IMP_NOT_R |
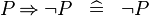 |
A | |
| * | SIMP_MULTI_IMP_AND |
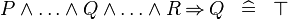 |
A | |
| * | SIMP_MULTI_IMP_AND_NOT_R |
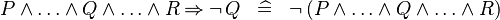 |
A | |
| * | SIMP_MULTI_IMP_AND_NOT_L |
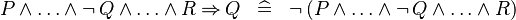 |
A | |
| * | SIMP_MULTI_EQV |
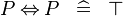 |
A | |
| * | SIMP_MULTI_EQV_NOT |
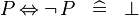 |
A | |
| * | SIMP_SPECIAL_NOT_BTRUE |
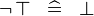 |
A | |
| * | SIMP_SPECIAL_NOT_BFALSE |
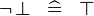 |
A | |
| * | SIMP_NOT_NOT |
 |
AM | |
| * | SIMP_NOTEQUAL |
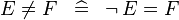 |
A | |
| * | SIMP_NOTIN |
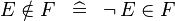 |
A | |
| * | SIMP_NOTSUBSET |
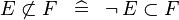 |
A | |
| * | SIMP_NOTSUBSETEQ |
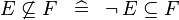 |
A | |
| * | SIMP_NOT_LE |
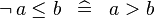 |
A | |
| * | SIMP_NOT_GE |
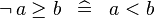 |
A | |
| * | SIMP_NOT_LT |
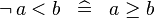 |
A | |
| * | SIMP_NOT_GT |
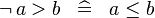 |
A | |
| * | SIMP_SPECIAL_NOT_EQUAL_FALSE_R |
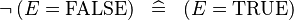 |
A | |
| * | SIMP_SPECIAL_NOT_EQUAL_FALSE_L |
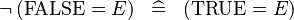 |
A | |
| * | SIMP_SPECIAL_NOT_EQUAL_TRUE_R |
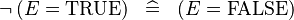 |
A | |
| * | SIMP_SPECIAL_NOT_EQUAL_TRUE_L |
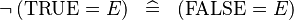 |
A | |
| * | SIMP_FORALL_AND |
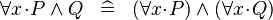 |
A | |
| * | SIMP_EXISTS_OR |
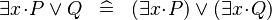 |
A | |
| * | SIMP_EXISTS_IMP |
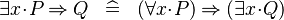 |
A | |
| * | SIMP_FORALL |
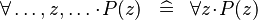 |
Quantified identifiers other than 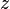 do not occur in do not occur in 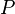 |
A |
| * | SIMP_EXISTS |
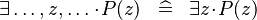 |
Quantified identifiers other than 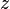 do not occur in do not occur in 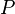 |
A |
| * | SIMP_MULTI_EQUAL |
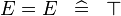 |
A | |
| * | SIMP_MULTI_NOTEQUAL |
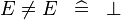 |
A | |
| * | SIMP_EQUAL_MAPSTO |
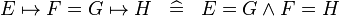 |
A | |
| * | SIMP_EQUAL_SING |
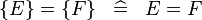 |
A | |
| * | SIMP_SPECIAL_EQUAL_TRUE |
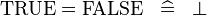 |
A | |
| * | SIMP_TYPE_SUBSETEQ |
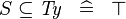 |
where  is a type expression is a type expression |
A |
| * | SIMP_SUBSETEQ_SING |
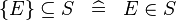 |
where  is a single expression is a single expression |
A |
| * | SIMP_SPECIAL_SUBSETEQ |
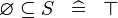 |
A | |
| * | SIMP_MULTI_SUBSETEQ |
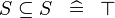 |
A | |
| * | SIMP_SUBSETEQ_BUNION |
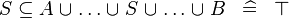 |
A | |
| * | SIMP_SUBSETEQ_BINTER |
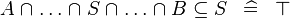 |
A | |
| * | DERIV_SUBSETEQ_BUNION |
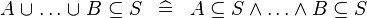 |
A | |
| * | DERIV_SUBSETEQ_BINTER |
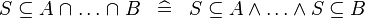 |
A | |
| * | SIMP_SPECIAL_IN |
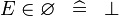 |
A | |
| * | SIMP_MULTI_IN |
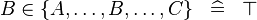 |
A | |
| * | SIMP_IN_SING |
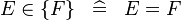 |
A | |
| * | SIMP_MULTI_SETENUM |
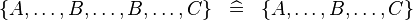 |
A | |
| * | SIMP_SPECIAL_BINTER |
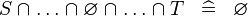 |
A | |
| * | SIMP_TYPE_BINTER |
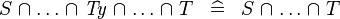 |
where  is a type expression is a type expression |
A |
| * | SIMP_MULTI_BINTER |
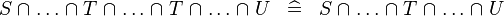 |
A | |
| * | SIMP_MULTI_EQUAL_BINTER |
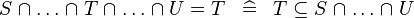 |
A | |
| * | SIMP_SPECIAL_BUNION |
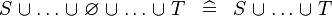 |
A | |
| * | SIMP_TYPE_BUNION |
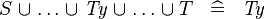 |
where  is a type expression is a type expression |
A |
| * | SIMP_MULTI_BUNION |
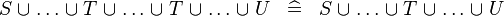 |
A | |
| * | SIMP_MULTI_EQUAL_BUNION |
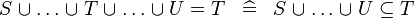 |
A | |
| * | SIMP_MULTI_SETMINUS |
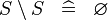 |
A | |
| * | SIMP_SPECIAL_SETMINUS_R |
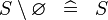 |
A | |
| * | SIMP_SPECIAL_SETMINUS_L |
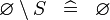 |
A | |
| * | SIMP_TYPE_SETMINUS |
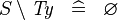 |
where  is a type expression is a type expression |
A |
| * | SIMP_TYPE_SETMINUS_SETMINUS |
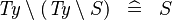 |
where  is a type expression is a type expression |
A |
| * | SIMP_KUNION_POW |
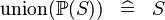 |
A | |
| * | SIMP_KUNION_POW1 |
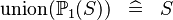 |
A | |
| * | SIMP_SPECIAL_KUNION |
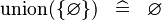 |
A | |
| * | SIMP_SPECIAL_QUNION |
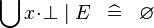 |
A | |
| * | SIMP_SPECIAL_KINTER |
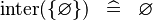 |
A | |
| * | SIMP_KINTER_POW |
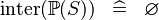 |
A | |
| * | SIMP_SPECIAL_POW |
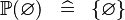 |
A | |
| * | SIMP_SPECIAL_POW1 |
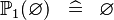 |
A | |
| * | SIMP_SPECIAL_CPROD_R |
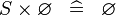 |
A | |
| * | SIMP_SPECIAL_CPROD_L |
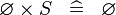 |
A | |
SIMP_COMPSET_EQUAL |
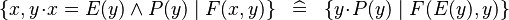 |
where  non free in non free in  and non free in and non free in 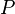 |
A | |
| * | SIMP_COMPSET_IN |
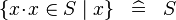 |
where  non free in non free in  |
A |
| * | SIMP_COMPSET_SUBSETEQ |
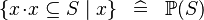 |
where  non free in non free in  |
A |
| * | SIMP_SPECIAL_COMPSET_BFALSE |
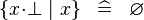 |
A | |
| * | SIMP_SPECIAL_COMPSET_BTRUE |
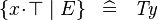 |
where the type of  is is  and and  is a maplet combination of locally-bound, pairwise-distinct bound identifiers is a maplet combination of locally-bound, pairwise-distinct bound identifiers |
A |
| * | SIMP_SUBSETEQ_COMPSET_L |
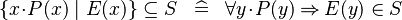 |
where 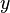 is fresh is fresh |
A |
| * | SIMP_IN_COMPSET |
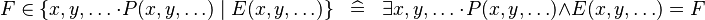 |
where  , , 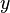 , , 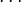 are not free in are not free in 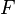 |
A |
| * | SIMP_IN_COMPSET_ONEPOINT |
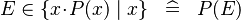 |
Equivalent to general simplification followed by One Point Rule application with the last conjunct predicate | A |
SIMP_SUBSETEQ_COMPSET_R |
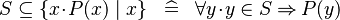 |
where 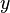 non free in non free in 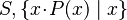 |
M | |
| * | SIMP_SPECIAL_OVERL |
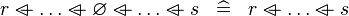 |
A | |
| * | SIMP_SPECIAL_KBOOL_BTRUE |
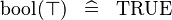 |
A | |
| * | SIMP_SPECIAL_KBOOL_BFALSE |
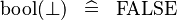 |
A | |
DISTRI_SUBSETEQ_BUNION_SING |
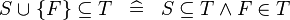 |
where 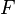 is a single expression is a single expression |
M | |
| * | DEF_FINITE |
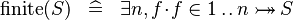 |
M | |
| * | SIMP_SPECIAL_FINITE |
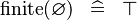 |
A | |
| * | SIMP_FINITE_SETENUM |
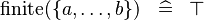 |
A | |
| * | SIMP_FINITE_BUNION |
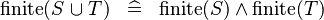 |
A | |
| * | SIMP_FINITE_POW |
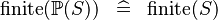 |
A | |
| * | DERIV_FINITE_CPROD |
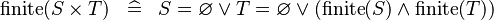 |
A | |
| * | SIMP_FINITE_CONVERSE |
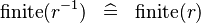 |
A | |
| * | SIMP_FINITE_UPTO |
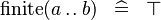 |
A | |
| * | SIMP_FINITE_ID |
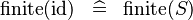 |
where 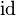 has type has type 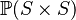 |
A |
| * | SIMP_FINITE_ID_DOMRES |
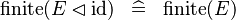 |
A | |
| * | SIMP_FINITE_PRJ1 |
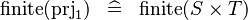 |
where 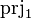 has type has type 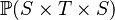 |
A |
| * | SIMP_FINITE_PRJ2 |
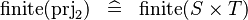 |
where 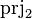 has type has type 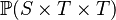 |
A |
| * | SIMP_FINITE_PRJ1_DOMRES |
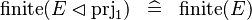 |
A | |
| * | SIMP_FINITE_PRJ2_DOMRES |
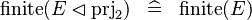 |
A | |
| * | SIMP_FINITE_NATURAL |
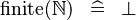 |
A | |
| * | SIMP_FINITE_NATURAL1 |
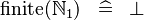 |
A | |
| * | SIMP_FINITE_INTEGER |
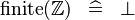 |
A | |
| * | SIMP_FINITE_BOOL |
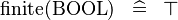 |
A | |
| * | SIMP_FINITE_LAMBDA |
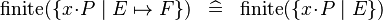 |
where  is a maplet combination of bound identifiers and expressions that are not bound by the comprehension set (i.e., is a maplet combination of bound identifiers and expressions that are not bound by the comprehension set (i.e.,  is syntactically injective) and all identifiers bound by the comprehension set that occur in is syntactically injective) and all identifiers bound by the comprehension set that occur in 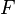 also occur in also occur in  |
A |
| * | SIMP_TYPE_IN |
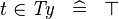 |
where  is a type expression is a type expression |
A |
| * | SIMP_SPECIAL_EQV_BTRUE |
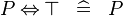 |
A | |
| * | SIMP_SPECIAL_EQV_BFALSE |
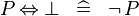 |
A | |
| * | DEF_SUBSET |
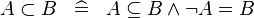 |
A | |
| * | SIMP_SPECIAL_SUBSET_R |
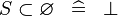 |
A | |
| * | SIMP_SPECIAL_SUBSET_L |
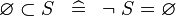 |
A | |
| * | SIMP_TYPE_SUBSET_L |
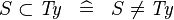 |
where  is a type expression is a type expression |
A |
| * | SIMP_MULTI_SUBSET |
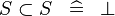 |
A | |
| * | SIMP_EQUAL_CONSTR |
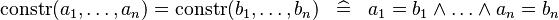 |
where 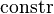 is a datatype constructor is a datatype constructor |
A |
| * | SIMP_EQUAL_CONSTR_DIFF |
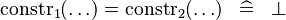 |
where 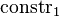 and and 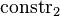 are different datatype constructors are different datatype constructors |
A |
| * | SIMP_DESTR_CONSTR |
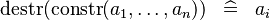 |
where 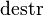 is the datatype destructor for the i-th argument of datatype constructor is the datatype destructor for the i-th argument of datatype constructor 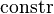 |
A |
| * | DISTRI_AND_OR |
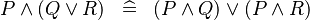 |
M | |
| * | DISTRI_OR_AND |
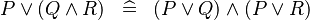 |
M | |
| * | DEF_OR |
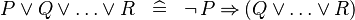 |
M | |
| * | DERIV_IMP |
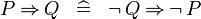 |
M | |
| * | DERIV_IMP_IMP |
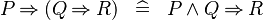 |
M | |
| * | DISTRI_IMP_AND |
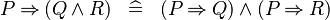 |
M | |
| * | DISTRI_IMP_OR |
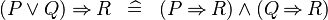 |
M | |
| * | DEF_EQV |
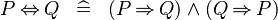 |
M | |
| * | DISTRI_NOT_AND |
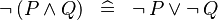 |
M | |
| * | DISTRI_NOT_OR |
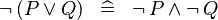 |
M | |
| * | DERIV_NOT_IMP |
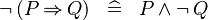 |
M | |
| * | DERIV_NOT_FORALL |
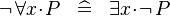 |
M | |
| * | DERIV_NOT_EXISTS |
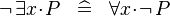 |
M | |
| * | DEF_IN_MAPSTO |
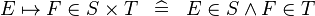 |
AM | |
| * | DEF_IN_POW |
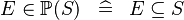 |
M | |
| * | DEF_IN_POW1 |
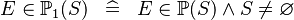 |
M | |
| * | DEF_SUBSETEQ |
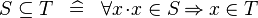 |
where  is not free in is not free in  or or 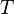 |
M |
| * | DEF_IN_BUNION |
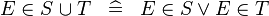 |
M | |
| * | DEF_IN_BINTER |
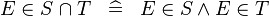 |
M | |
| * | DEF_IN_SETMINUS |
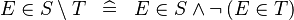 |
M | |
| * | DEF_IN_SETENUM |
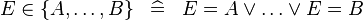 |
M | |
| * | DEF_IN_KUNION |
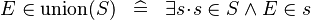 |
where  is fresh is fresh |
M |
| * | DEF_IN_QUNION |
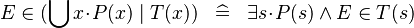 |
where  is fresh is fresh |
M |
| * | DEF_IN_KINTER |
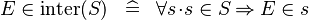 |
where  is fresh is fresh |
M |
| * | DEF_IN_QINTER |
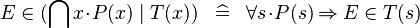 |
where  is fresh is fresh |
M |
| * | DEF_IN_UPTO |
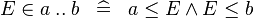 |
M | |
| * | DISTRI_BUNION_BINTER |
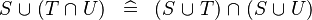 |
M | |
| * | DISTRI_BINTER_BUNION |
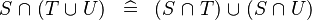 |
M | |
DISTRI_BINTER_SETMINUS |
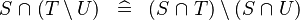 |
M | ||
DISTRI_SETMINUS_BUNION |
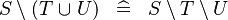 |
M | ||
| * | DERIV_TYPE_SETMINUS_BINTER |
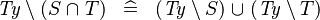 |
where  is a type expression is a type expression |
M |
| * | DERIV_TYPE_SETMINUS_BUNION |
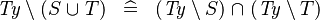 |
where  is a type expression is a type expression |
M |
| * | DERIV_TYPE_SETMINUS_SETMINUS |
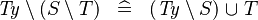 |
where  is a type expression is a type expression |
M |
DISTRI_CPROD_BINTER |
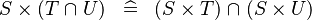 |
M | ||
DISTRI_CPROD_BUNION |
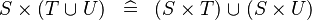 |
M | ||
DISTRI_CPROD_SETMINUS |
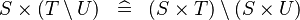 |
M | ||
| * | DERIV_SUBSETEQ |
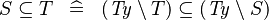 |
where 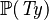 is the type of is the type of  and and 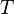 |
M |
| * | DERIV_EQUAL |
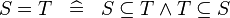 |
where 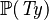 is the type of is the type of  and and 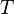 |
M |
| * | DERIV_SUBSETEQ_SETMINUS_L |
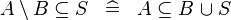 |
M | |
| * | DERIV_SUBSETEQ_SETMINUS_R |
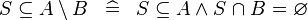 |
M | |
| * | DEF_PARTITION |
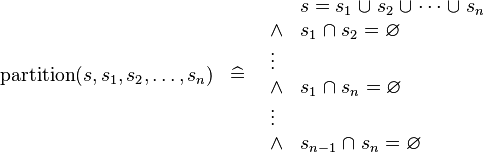 |
AM | |
| * | SIMP_EMPTY_PARTITION |
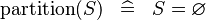 |
A | |
| * | SIMP_SINGLE_PARTITION |
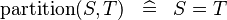 |
A | |
| * | DEF_EQUAL_CARD |
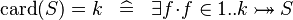 |
also works for 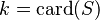 |
M |
| * | SIMP_EQUAL_CARD |
 |
M |
Relation Rewrite Rules
Rules that are marked with a * in the first column are implemented in the latest version of Rodin. Rules without a * are planned to be implemented in future versions. Other conventions used in these tables are described in The_Proving_Perspective_(Rodin_User_Manual)#Rewrite_Rules.
| Name | Rule | Side Condition | A/M | |
|---|---|---|---|---|
| * | SIMP_DOM_SETENUM |
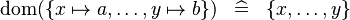 |
A | |
| * | SIMP_DOM_CONVERSE |
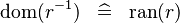 |
A | |
| * | SIMP_RAN_SETENUM |
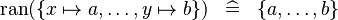 |
A | |
| * | SIMP_RAN_CONVERSE |
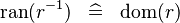 |
A | |
| * | SIMP_SPECIAL_OVERL |
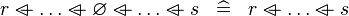 |
A | |
| * | SIMP_MULTI_OVERL |
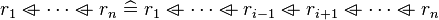 |
there is a 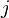 such that such that 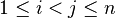 and and 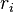 and and 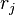 are syntactically equal. are syntactically equal. |
A |
| * | SIMP_TYPE_OVERL_CPROD |
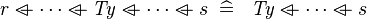 |
where  is a type expression is a type expression |
A |
| * | SIMP_SPECIAL_DOMRES_L |
 |
A | |
| * | SIMP_SPECIAL_DOMRES_R |
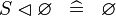 |
A | |
| * | SIMP_TYPE_DOMRES |
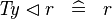 |
where  is a type expression is a type expression |
A |
| * | SIMP_MULTI_DOMRES_DOM |
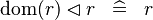 |
A | |
| * | SIMP_MULTI_DOMRES_RAN |
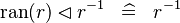 |
A | |
| * | SIMP_DOMRES_DOMRES_ID |
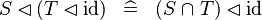 |
A | |
| * | SIMP_DOMRES_DOMSUB_ID |
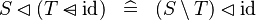 |
A | |
| * | SIMP_SPECIAL_RANRES_R |
 |
A | |
| * | SIMP_SPECIAL_RANRES_L |
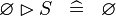 |
A | |
| * | SIMP_TYPE_RANRES |
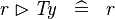 |
where  is a type expression is a type expression |
A |
| * | SIMP_MULTI_RANRES_RAN |
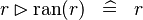 |
A | |
| * | SIMP_MULTI_RANRES_DOM |
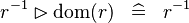 |
A | |
| * | SIMP_RANRES_ID |
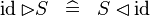 |
A | |
| * | SIMP_RANSUB_ID |
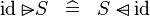 |
A | |
| * | SIMP_RANRES_DOMRES_ID |
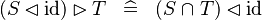 |
A | |
| * | SIMP_RANRES_DOMSUB_ID |
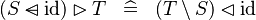 |
A | |
| * | SIMP_SPECIAL_DOMSUB_L |
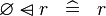 |
A | |
| * | SIMP_SPECIAL_DOMSUB_R |
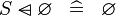 |
A | |
| * | SIMP_TYPE_DOMSUB |
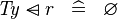 |
where  is a type expression is a type expression |
A |
| * | SIMP_MULTI_DOMSUB_DOM |
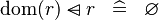 |
A | |
| * | SIMP_MULTI_DOMSUB_RAN |
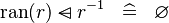 |
A | |
| * | SIMP_DOMSUB_DOMRES_ID |
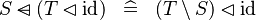 |
A | |
| * | SIMP_DOMSUB_DOMSUB_ID |
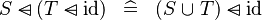 |
A | |
| * | SIMP_SPECIAL_RANSUB_R |
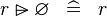 |
A | |
| * | SIMP_SPECIAL_RANSUB_L |
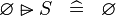 |
A | |
| * | SIMP_TYPE_RANSUB |
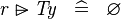 |
where  is a type expression is a type expression |
A |
| * | SIMP_MULTI_RANSUB_DOM |
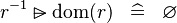 |
A | |
| * | SIMP_MULTI_RANSUB_RAN |
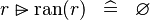 |
A | |
| * | SIMP_RANSUB_DOMRES_ID |
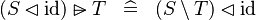 |
A | |
| * | SIMP_RANSUB_DOMSUB_ID |
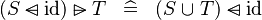 |
A | |
| * | SIMP_SPECIAL_FCOMP |
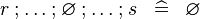 |
A | |
| * | SIMP_TYPE_FCOMP_ID |
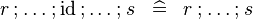 |
A | |
| * | SIMP_TYPE_FCOMP_R |
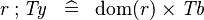 |
where  is a type expression equal to is a type expression equal to 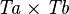 |
A |
| * | SIMP_TYPE_FCOMP_L |
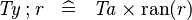 |
where  is a type expression equal to is a type expression equal to 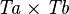 |
A |
| * | SIMP_FCOMP_ID |
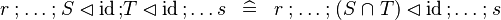 |
A | |
| * | SIMP_SPECIAL_BCOMP |
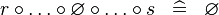 |
A | |
| * | SIMP_TYPE_BCOMP_ID |
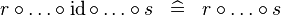 |
A | |
| * | SIMP_TYPE_BCOMP_L |
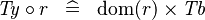 |
where  is a type expression equal to is a type expression equal to 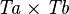 |
A |
| * | SIMP_TYPE_BCOMP_R |
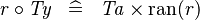 |
where  is a type expression equal to is a type expression equal to 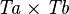 |
A |
| * | SIMP_BCOMP_ID |
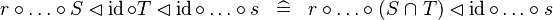 |
A | |
| * | SIMP_SPECIAL_DPROD_R |
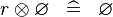 |
A | |
| * | SIMP_SPECIAL_DPROD_L |
 |
A | |
| * | SIMP_DPROD_CPROD |
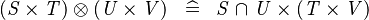 |
A | |
| * | SIMP_SPECIAL_PPROD_R |
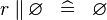 |
A | |
| * | SIMP_SPECIAL_PPROD_L |
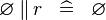 |
A | |
| * | SIMP_PPROD_CPROD |
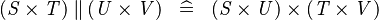 |
A | |
| * | SIMP_SPECIAL_RELIMAGE_R |
![r[\emptyset ] \;\;\defi\;\; \emptyset](/images/math/b/9/a/b9aaf14a5527d53ff1febab3e8883f03.png) |
A | |
| * | SIMP_SPECIAL_RELIMAGE_L |
![\emptyset [S] \;\;\defi\;\; \emptyset](/images/math/6/4/8/648fbd380df0ae4c5d64da8bef51ee2d.png) |
A | |
| * | SIMP_TYPE_RELIMAGE |
![r[Ty] \;\;\defi\;\; \ran (r)](/images/math/0/2/1/02153b3e9f952be7157a4d4e336374a7.png) |
where  is a type expression is a type expression |
A |
| * | SIMP_MULTI_RELIMAGE_DOM |
![r[\dom (r)] \;\;\defi\;\; \ran (r)](/images/math/0/3/4/0346b1b9c1146a8343fa2d18e1732769.png) |
A | |
| * | SIMP_RELIMAGE_ID |
![\id[T] \;\;\defi\;\; T](/images/math/4/0/0/4009c72979487233368b217afa41d8ad.png) |
A | |
| * | SIMP_RELIMAGE_DOMRES_ID |
![(S \domres \id)[T] \;\;\defi\;\; S \binter T](/images/math/b/e/2/be2ea9770f745da9730119cc0e6c7be3.png) |
A | |
| * | SIMP_RELIMAGE_DOMSUB_ID |
![(S \domsub \id)[T] \;\;\defi\;\; T \setminus S](/images/math/6/1/4/6143619949a6ea25351813e711f4f395.png) |
A | |
| * | SIMP_MULTI_RELIMAGE_CPROD_SING |
![(\{ E\} \cprod S)[\{ E\} ] \;\;\defi\;\; S](/images/math/c/5/2/c526fc7db223ce0bfe920622d54d64e0.png) |
where  is a single expression is a single expression |
A |
| * | SIMP_MULTI_RELIMAGE_SING_MAPSTO |
![\{ E \mapsto F\} [\{ E\} ] \;\;\defi\;\; \{ F\}](/images/math/e/2/c/e2c3111e1660139c0d07f75c30de0e5c.png) |
where  is a single expression is a single expression |
A |
| * | SIMP_MULTI_RELIMAGE_CONVERSE_RANSUB |
![(r \ransub S)^{-1} [S] \;\;\defi\;\; \emptyset](/images/math/0/d/8/0d87a3a40feb382450061c80f9ed103e.png) |
A | |
| * | SIMP_MULTI_RELIMAGE_CONVERSE_RANRES |
![(r \ranres S)^{-1} [S] \;\;\defi\;\; r^{-1} [S]](/images/math/1/7/4/174952bb78d6d7afd42ee6a53ed2ac78.png) |
A | |
| * | SIMP_RELIMAGE_CONVERSE_DOMSUB |
![(S \domsub r)^{-1} [T] \;\;\defi\;\; r^{-1} [T] \setminus S](/images/math/3/4/2/342512ec589776fd0aae93fe8eb732e6.png) |
A | |
DERIV_RELIMAGE_RANSUB |
![(r \ransub S)[T] \;\;\defi\;\; r[T] \setminus S](/images/math/5/9/3/5933212d9aad4f59b7641ea383b31a91.png) |
M | ||
DERIV_RELIMAGE_RANRES |
![(r \ranres S)[T] \;\;\defi\;\; r[T] \binter S](/images/math/1/9/9/1994ec5d3fa539db498124fe8fd4a27d.png) |
M | ||
| * | SIMP_MULTI_RELIMAGE_DOMSUB |
![(S \domsub r)[S] \;\;\defi\;\; \emptyset](/images/math/b/f/3/bf31fb9e2da1545464bd5baecc397c01.png) |
A | |
DERIV_RELIMAGE_DOMSUB |
![(S \domsub r)[T] \;\;\defi\;\; r[T \setminus S]](/images/math/f/2/4/f2407e5c136829c08c1bc390d74a77fe.png) |
M | ||
DERIV_RELIMAGE_DOMRES |
![(S \domres r)[T] \;\;\defi\;\; r[S \binter T]](/images/math/8/4/0/840633e87abc3f54638ede200920f377.png) |
M | ||
| * | SIMP_SPECIAL_CONVERSE |
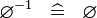 |
A | |
| * | SIMP_CONVERSE_ID |
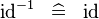 |
A | |
| * | SIMP_CONVERSE_CPROD |
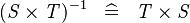 |
A | |
| * | SIMP_CONVERSE_SETENUM |
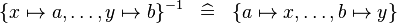 |
A | |
| * | SIMP_CONVERSE_COMPSET |
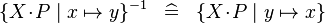 |
A | |
| * | SIMP_DOM_ID |
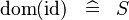 |
where 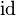 has type has type 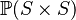 |
A |
| * | SIMP_RAN_ID |
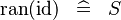 |
where 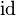 has type has type 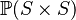 |
A |
| * | SIMP_FCOMP_ID_L |
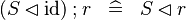 |
A | |
| * | SIMP_FCOMP_ID_R |
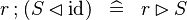 |
A | |
| * | SIMP_SPECIAL_REL_R |
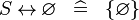 |
idem for operators 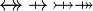 |
A |
| * | SIMP_SPECIAL_REL_L |
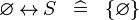 |
idem for operators 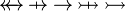 |
A |
| * | SIMP_FUNIMAGE_PRJ1 |
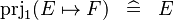 |
A | |
| * | SIMP_FUNIMAGE_PRJ2 |
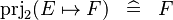 |
A | |
| * | SIMP_DOM_PRJ1 |
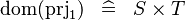 |
where 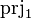 has type has type 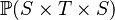 |
A |
| * | SIMP_DOM_PRJ2 |
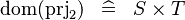 |
where 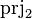 has type has type 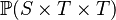 |
A |
| * | SIMP_RAN_PRJ1 |
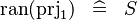 |
where 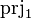 has type has type 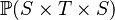 |
A |
| * | SIMP_RAN_PRJ2 |
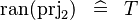 |
where 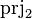 has type has type 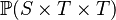 |
A |
| * | SIMP_FUNIMAGE_LAMBDA |
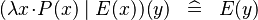 |
A | |
| * | SIMP_DOM_LAMBDA |
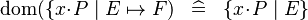 |
A | |
| * | SIMP_RAN_LAMBDA |
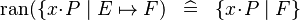 |
A | |
| * | SIMP_IN_FUNIMAGE |
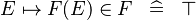 |
A | |
| * | SIMP_IN_FUNIMAGE_CONVERSE_L |
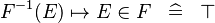 |
A | |
| * | SIMP_IN_FUNIMAGE_CONVERSE_R |
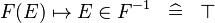 |
A | |
| * | SIMP_MULTI_FUNIMAGE_SETENUM_LL |
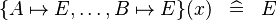 |
A | |
| * | SIMP_MULTI_FUNIMAGE_SETENUM_LR |
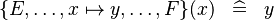 |
A | |
| * | SIMP_MULTI_FUNIMAGE_OVERL_SETENUM |
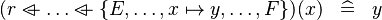 |
A | |
| * | SIMP_MULTI_FUNIMAGE_BUNION_SETENUM |
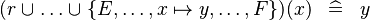 |
A | |
| * | SIMP_FUNIMAGE_CPROD |
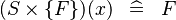 |
A | |
| * | SIMP_FUNIMAGE_ID |
 |
A | |
| * | SIMP_FUNIMAGE_FUNIMAGE_CONVERSE |
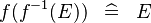 |
A | |
| * | SIMP_FUNIMAGE_CONVERSE_FUNIMAGE |
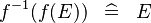 |
A | |
| * | SIMP_FUNIMAGE_FUNIMAGE_CONVERSE_SETENUM |
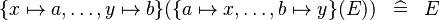 |
A | |
| * | SIMP_FUNIMAGE_DOMRES |
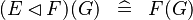 |
with hypothesis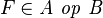 where where 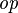 is one of is one of 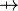 , ,  , , 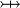 , , 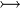 , , 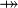 , , 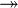 , , 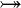 . . |
AM |
| * | SIMP_FUNIMAGE_DOMSUB |
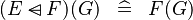 |
with hypothesis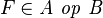 where where 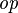 is one of is one of 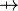 , , 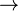 , , 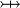 , , 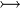 , , 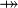 , , 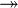 , , 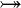 . . |
AM |
| * | SIMP_FUNIMAGE_RANRES |
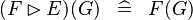 |
with hypothesis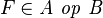 where where 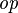 is one of is one of 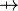 , , 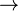 , , 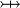 , , 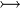 , , 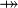 , , 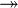 , , 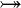 . . |
AM |
| * | SIMP_FUNIMAGE_RANSUB |
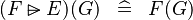 |
with hypothesis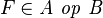 where where 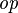 is one of is one of 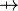 , , 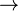 , , 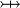 , , 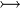 , , 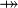 , , 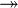 , , 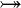 . . |
AM |
| * | SIMP_FUNIMAGE_SETMINUS |
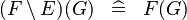 |
with hypothesis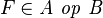 where where 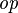 is one of is one of 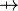 , , 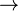 , , 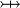 , , 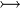 , , 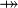 , , 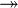 , , 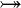 . . |
AM |
| * | DEF_EQUAL_FUNIMAGE |
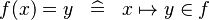 |
M | |
| * | DEF_BCOMP |
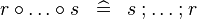 |
M | |
DERIV_ID_SING |
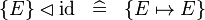 |
where  is a single expression is a single expression |
M | |
| * | SIMP_SPECIAL_DOM |
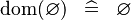 |
A | |
| * | SIMP_SPECIAL_RAN |
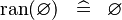 |
A | |
| * | SIMP_CONVERSE_CONVERSE |
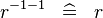 |
A | |
| * | DERIV_RELIMAGE_FCOMP |
![(p \fcomp q)[s] \;\;\defi\;\; q[p[s]]](/images/math/d/5/2/d525cb240947f85af66b077f0894364c.png) |
M | |
| * | DERIV_FCOMP_DOMRES |
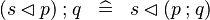 |
M | |
| * | DERIV_FCOMP_DOMSUB |
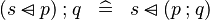 |
M | |
| * | DERIV_FCOMP_RANRES |
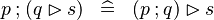 |
M | |
| * | DERIV_FCOMP_RANSUB |
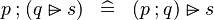 |
M | |
DERIV_FCOMP_SING |
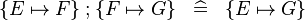 |
A | ||
| * | SIMP_SPECIAL_EQUAL_RELDOMRAN |
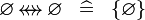 |
idem for operators  |
A |
| * | SIMP_TYPE_DOM |
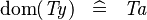 |
where  is a type expression equal to is a type expression equal to 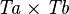 |
A |
| * | SIMP_TYPE_RAN |
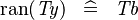 |
where  is a type expression equal to is a type expression equal to 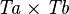 |
A |
| * | SIMP_MULTI_DOM_CPROD |
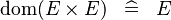 |
A | |
| * | SIMP_MULTI_RAN_CPROD |
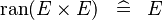 |
A | |
| * | SIMP_MULTI_DOM_DOMRES |
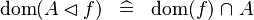 |
A | |
| * | SIMP_MULTI_DOM_DOMSUB |
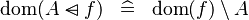 |
A | |
| * | SIMP_MULTI_RAN_RANRES |
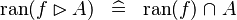 |
A | |
| * | SIMP_MULTI_RAN_RANSUB |
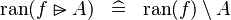 |
A | |
| * | DEF_IN_DOM |
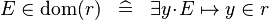 |
M | |
| * | DEF_IN_RAN |
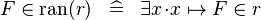 |
M | |
| * | DEF_IN_CONVERSE |
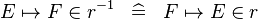 |
M | |
| * | DEF_IN_DOMRES |
 |
M | |
| * | DEF_IN_RANRES |
 |
M | |
| * | DEF_IN_DOMSUB |
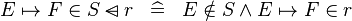 |
M | |
| * | DEF_IN_RANSUB |
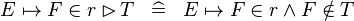 |
M | |
| * | DEF_IN_RELIMAGE |
![F \in r[w] \;\;\defi\;\; \exists x \qdot x \in w \land x \mapsto F \in r](/images/math/e/a/7/ea7840f0b824a8db50a6356a02b00904.png) |
M | |
| * | DEF_IN_FCOMP |
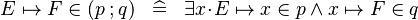 |
M | |
| * | DEF_OVERL |
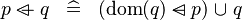 |
M | |
| * | DEF_IN_ID |
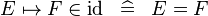 |
M | |
| * | DEF_IN_DPROD |
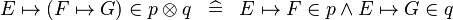 |
M | |
| * | DEF_IN_PPROD |
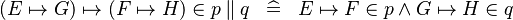 |
M | |
| * | DEF_IN_REL |
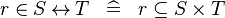 |
M | |
| * | DEF_IN_RELDOM |
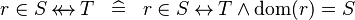 |
M | |
| * | DEF_IN_RELRAN |
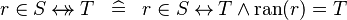 |
M | |
| * | DEF_IN_RELDOMRAN |
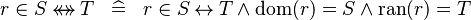 |
M | |
| * | DEF_IN_FCT |
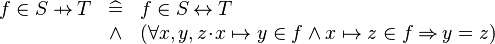 |
M | |
| * | DEF_IN_TFCT |
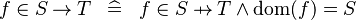 |
M | |
| * | DEF_IN_INJ |
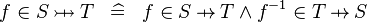 |
M | |
| * | DEF_IN_TINJ |
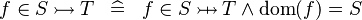 |
M | |
| * | DEF_IN_SURJ |
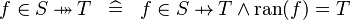 |
M | |
| * | DEF_IN_TSURJ |
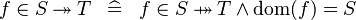 |
M | |
| * | DEF_IN_BIJ |
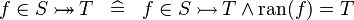 |
M | |
DISTRI_BCOMP_BUNION |
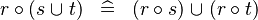 |
M | ||
| * | DISTRI_FCOMP_BUNION_R |
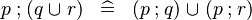 |
M | |
| * | DISTRI_FCOMP_BUNION_L |
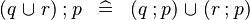 |
M | |
DISTRI_DPROD_BUNION |
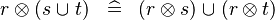 |
M | ||
DISTRI_DPROD_BINTER |
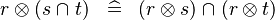 |
M | ||
DISTRI_DPROD_SETMINUS |
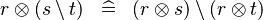 |
M | ||
DISTRI_DPROD_OVERL |
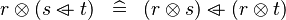 |
M | ||
DISTRI_PPROD_BUNION |
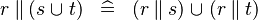 |
M | ||
DISTRI_PPROD_BINTER |
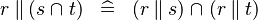 |
M | ||
DISTRI_PPROD_SETMINUS |
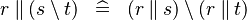 |
M | ||
DISTRI_PPROD_OVERL |
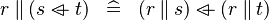 |
M | ||
DISTRI_OVERL_BUNION_L |
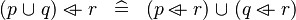 |
M | ||
DISTRI_OVERL_BINTER_L |
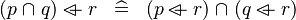 |
M | ||
| * | DISTRI_DOMRES_BUNION_R |
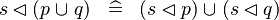 |
M | |
| * | DISTRI_DOMRES_BUNION_L |
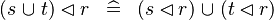 |
M | |
| * | DISTRI_DOMRES_BINTER_R |
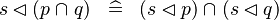 |
M | |
| * | DISTRI_DOMRES_BINTER_L |
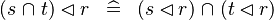 |
M | |
DISTRI_DOMRES_SETMINUS_R |
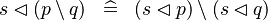 |
M | ||
DISTRI_DOMRES_SETMINUS_L |
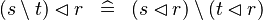 |
M | ||
DISTRI_DOMRES_DPROD |
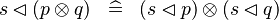 |
M | ||
DISTRI_DOMRES_OVERL |
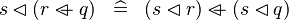 |
M | ||
| * | DISTRI_DOMSUB_BUNION_R |
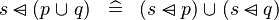 |
M | |
| * | DISTRI_DOMSUB_BUNION_L |
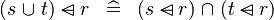 |
M | |
| * | DISTRI_DOMSUB_BINTER_R |
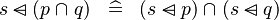 |
M | |
| * | DISTRI_DOMSUB_BINTER_L |
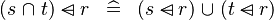 |
M | |
DISTRI_DOMSUB_DPROD |
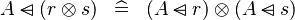 |
M | ||
DISTRI_DOMSUB_OVERL |
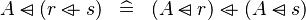 |
M | ||
| * | DISTRI_RANRES_BUNION_R |
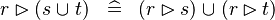 |
M | |
| * | DISTRI_RANRES_BUNION_L |
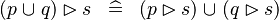 |
M | |
| * | DISTRI_RANRES_BINTER_R |
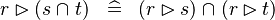 |
M | |
| * | DISTRI_RANRES_BINTER_L |
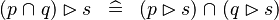 |
M | |
DISTRI_RANRES_SETMINUS_R |
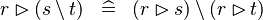 |
M | ||
DISTRI_RANRES_SETMINUS_L |
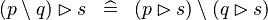 |
M | ||
| * | DISTRI_RANSUB_BUNION_R |
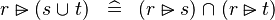 |
M | |
| * | DISTRI_RANSUB_BUNION_L |
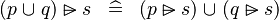 |
M | |
| * | DISTRI_RANSUB_BINTER_R |
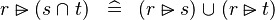 |
M | |
| * | DISTRI_RANSUB_BINTER_L |
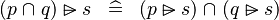 |
M | |
| * | DISTRI_CONVERSE_BUNION |
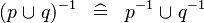 |
M | |
DISTRI_CONVERSE_BINTER |
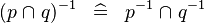 |
M | ||
DISTRI_CONVERSE_SETMINUS |
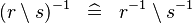 |
M | ||
DISTRI_CONVERSE_BCOMP |
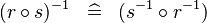 |
M | ||
DISTRI_CONVERSE_FCOMP |
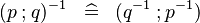 |
M | ||
DISTRI_CONVERSE_PPROD |
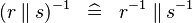 |
M | ||
DISTRI_CONVERSE_DOMRES |
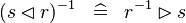 |
M | ||
DISTRI_CONVERSE_DOMSUB |
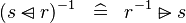 |
M | ||
DISTRI_CONVERSE_RANRES |
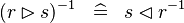 |
M | ||
DISTRI_CONVERSE_RANSUB |
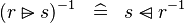 |
M | ||
| * | DISTRI_DOM_BUNION |
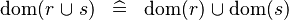 |
M | |
| * | DISTRI_RAN_BUNION |
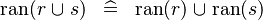 |
M | |
| * | DISTRI_RELIMAGE_BUNION_R |
![r[S \bunion T] \;\;\defi\;\; r[S] \bunion r[T]](/images/math/6/7/5/675105d6ac145c32895450ddb1a9515f.png) |
M | |
| * | DISTRI_RELIMAGE_BUNION_L |
![(p \bunion q)[S] \;\;\defi\;\; p[S] \bunion q[S]](/images/math/c/d/a/cdad0c6221ccb102d4f674695d7ff79c.png) |
M | |
| * | DERIV_DOM_TOTALREL |
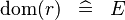 |
with hypothesis 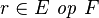 , where , where 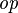 is one of is one of 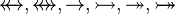 |
M |
DERIV_RAN_SURJREL |
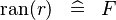 |
with hypothesis 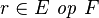 , where , where 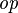 is one of is one of 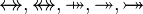 |
M | |
| * | DERIV_PRJ1_SURJ |
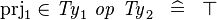 |
where 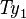 and and 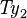 are types and are types and 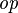 is one of is one of 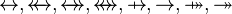 |
A |
| * | DERIV_PRJ2_SURJ |
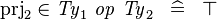 |
where 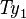 and and 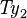 are types and are types and 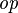 is one of is one of 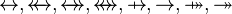 |
A |
| * | DERIV_ID_BIJ |
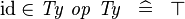 |
where  is a type and is a type and 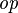 is any arrow is any arrow |
A |
| * | SIMP_MAPSTO_PRJ1_PRJ2 |
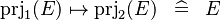 |
A | |
DERIV_EXPAND_PRJS |
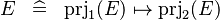 |
M | ||
| * | SIMP_DOM_SUCC |
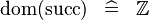 |
A | |
| * | SIMP_RAN_SUCC |
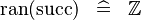 |
A | |
| * | DERIV_MULTI_IN_BUNION |
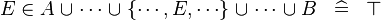 |
A | |
| * | DERIV_MULTI_IN_SETMINUS |
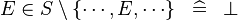 |
A | |
| * | DEF_PRED |
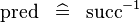 |
A | |
| * | SIMP_SPECIAL_IN_ID |
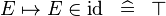 |
A | |
| * | SIMP_SPECIAL_IN_SETMINUS_ID |
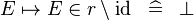 |
A | |
| * | SIMP_SPECIAL_IN_DOMRES_ID |
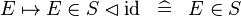 |
A | |
| * | SIMP_SPECIAL_IN_SETMINUS_DOMRES_ID |
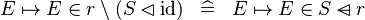 |
A |
Empty Set Rewrite Rules
Rules that are marked with a * in the first column are implemented in the latest version of Rodin. Rules without a * are planned to be implemented in future versions. Other conventions used in these tables are described in The_Proving_Perspective_(Rodin_User_Manual)#Rewrite_Rules.
All rewrite rules that match the pattern  are also applicable to predicates of the form
are also applicable to predicates of the form  and
and  , as these predicates are equivalent. All rewrite rules that match the pattern
, as these predicates are equivalent. All rewrite rules that match the pattern 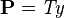 are also applicable to predicates of the form
are also applicable to predicates of the form 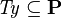 and
and 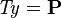 , as these predicates are equivalent.
, as these predicates are equivalent.
| Name | Rule | Side Condition | A/M | |
|---|---|---|---|---|
| * | DEF_SPECIAL_NOT_EQUAL |
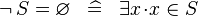 |
where  is not free in is not free in  |
M |
| * | SIMP_SETENUM_EQUAL_EMPTY |
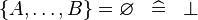 |
A | |
| * | SIMP_SPECIAL_EQUAL_COMPSET |
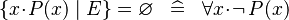 |
A | |
| * | SIMP_BINTER_EQUAL_TYPE |
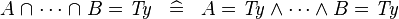 |
where  is a type expression is a type expression |
A |
| * | SIMP_BINTER_SING_EQUAL_EMPTY |
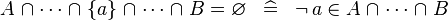 |
A | |
| * | SIMP_BINTER_SETMINUS_EQUAL_EMPTY |
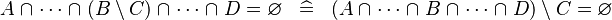 |
A | |
| * | SIMP_BUNION_EQUAL_EMPTY |
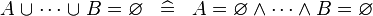 |
A | |
| * | SIMP_SETMINUS_EQUAL_EMPTY |
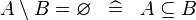 |
A | |
| * | SIMP_SETMINUS_EQUAL_TYPE |
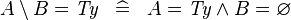 |
where  is a type expression is a type expression |
A |
| * | SIMP_POW_EQUAL_EMPTY |
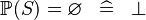 |
A | |
| * | SIMP_POW1_EQUAL_EMPTY |
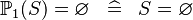 |
A | |
| * | SIMP_KINTER_EQUAL_TYPE |
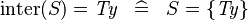 |
where  is a type expression is a type expression |
A |
| * | SIMP_KUNION_EQUAL_EMPTY |
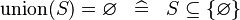 |
A | |
| * | SIMP_QINTER_EQUAL_TYPE |
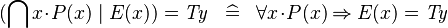 |
where  is a type expression is a type expression |
A |
| * | SIMP_QUNION_EQUAL_EMPTY |
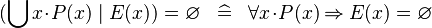 |
A | |
| * | SIMP_NATURAL_EQUAL_EMPTY |
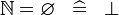 |
A | |
| * | SIMP_NATURAL1_EQUAL_EMPTY |
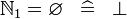 |
A | |
| * | SIMP_TYPE_EQUAL_EMPTY |
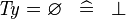 |
where  is a type expression is a type expression |
A |
| * | SIMP_CPROD_EQUAL_EMPTY |
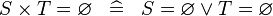 |
A | |
| * | SIMP_CPROD_EQUAL_TYPE |
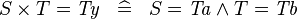 |
where  is a type expression equal to is a type expression equal to 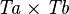 |
A |
| * | SIMP_UPTO_EQUAL_EMPTY |
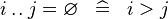 |
A | |
| * | SIMP_UPTO_EQUAL_INTEGER |
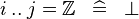 |
A | |
| * | SIMP_UPTO_EQUAL_NATURAL |
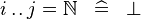 |
A | |
| * | SIMP_UPTO_EQUAL_NATURAL1 |
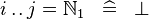 |
A | |
| * | SIMP_SPECIAL_EQUAL_REL |
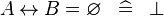 |
idem for operators 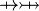 |
A |
SIMP_TYPE_EQUAL_REL |
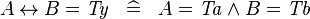 |
where  is a type expression equal to is a type expression equal to 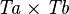 |
A | |
| * | SIMP_SPECIAL_EQUAL_RELDOM |
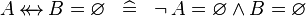 |
idem for operator 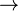 |
A |
SIMP_TYPE_EQUAL_RELDOMRAN |
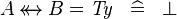 |
where  is a type expression, idem for operator is a type expression, idem for operator 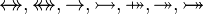 |
A | |
| * | SIMP_SREL_EQUAL_EMPTY |
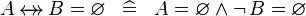 |
A | |
| * | SIMP_STREL_EQUAL_EMPTY |
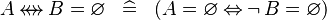 |
A | |
| * | SIMP_DOM_EQUAL_EMPTY |
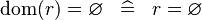 |
A | |
| * | SIMP_RAN_EQUAL_EMPTY |
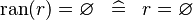 |
A | |
| * | SIMP_FCOMP_EQUAL_EMPTY |
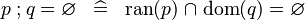 |
A | |
| * | SIMP_BCOMP_EQUAL_EMPTY |
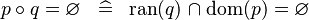 |
A | |
| * | SIMP_DOMRES_EQUAL_EMPTY |
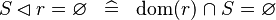 |
A | |
| * | SIMP_DOMRES_EQUAL_TYPE |
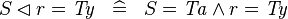 |
where  is a type expression equal to is a type expression equal to 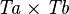 |
A |
| * | SIMP_DOMSUB_EQUAL_EMPTY |
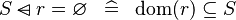 |
A | |
| * | SIMP_DOMSUB_EQUAL_TYPE |
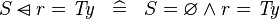 |
where  is a type expression is a type expression |
A |
| * | SIMP_RANRES_EQUAL_EMPTY |
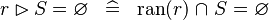 |
A | |
| * | SIMP_RANRES_EQUAL_TYPE |
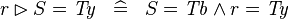 |
where  is a type expression equal to is a type expression equal to 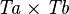 |
A |
| * | SIMP_RANSUB_EQUAL_EMPTY |
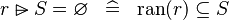 |
A | |
| * | SIMP_RANSUB_EQUAL_TYPE |
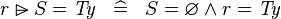 |
where  is a type expression is a type expression |
A |
| * | SIMP_CONVERSE_EQUAL_EMPTY |
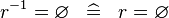 |
A | |
| * | SIMP_CONVERSE_EQUAL_TYPE |
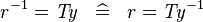 |
where  is a type expression is a type expression |
A |
| * | SIMP_RELIMAGE_EQUAL_EMPTY |
![r[S] = \emptyset \;\;\defi\;\; S \domres r = \emptyset](/images/math/3/8/f/38f444db2941b8e696a89faeec9b7623.png) |
A | |
| * | SIMP_OVERL_EQUAL_EMPTY |
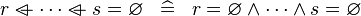 |
A | |
| * | SIMP_DPROD_EQUAL_EMPTY |
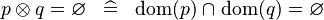 |
A | |
| * | SIMP_DPROD_EQUAL_TYPE |
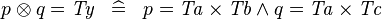 |
where  is a type expression equal to is a type expression equal to 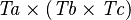 |
A |
| * | SIMP_PPROD_EQUAL_EMPTY |
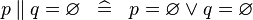 |
A | |
| * | SIMP_PPROD_EQUAL_TYPE |
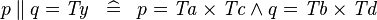 |
where  is a type expression equal to is a type expression equal to 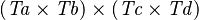 |
A |
| * | SIMP_ID_EQUAL_EMPTY |
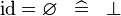 |
A | |
| * | SIMP_PRJ1_EQUAL_EMPTY |
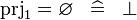 |
A | |
| * | SIMP_PRJ2_EQUAL_EMPTY |
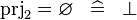 |
A |
Arithmetic Rewrite Rules
Rules that are marked with a * in the first column are implemented in the latest version of Rodin. Rules without a * are planned to be implemented in future versions. Other conventions used in these tables are described in The_Proving_Perspective_(Rodin_User_Manual)#Rewrite_Rules.
| Name | Rule | Side Condition | A/M | |
|---|---|---|---|---|
| * | SIMP_SPECIAL_MOD_0 |
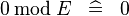 |
A | |
| * | SIMP_SPECIAL_MOD_1 |
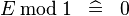 |
A | |
| * | SIMP_MIN_SING |
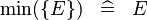 |
where  is a single expression is a single expression |
A |
| * | SIMP_MAX_SING |
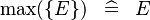 |
where  is a single expression is a single expression |
A |
| * | SIMP_MIN_NATURAL |
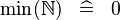 |
A | |
| * | SIMP_MIN_NATURAL1 |
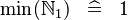 |
A | |
| * | SIMP_MIN_BUNION_SING |
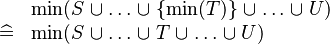 |
A | |
| * | SIMP_MAX_BUNION_SING |
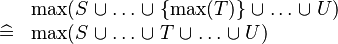 |
A | |
| * | SIMP_MIN_UPTO |
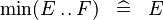 |
A | |
| * | SIMP_MAX_UPTO |
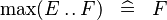 |
A | |
| * | SIMP_MIN_IN |
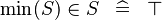 |
A | |
| * | SIMP_MAX_IN |
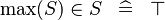 |
A | |
| * | SIMP_LIT_MIN |
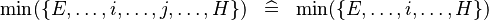 |
where 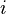 and and 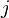 are literals and are literals and 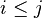 |
A |
| * | SIMP_LIT_MAX |
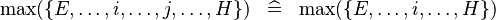 |
where 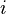 and and 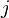 are literals and are literals and 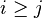 |
A |
| * | SIMP_SPECIAL_CARD |
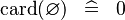 |
A | |
| * | SIMP_CARD_SING |
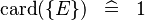 |
where  is a single expression is a single expression |
A |
| * | SIMP_SPECIAL_EQUAL_CARD |
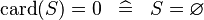 |
A | |
| * | SIMP_CARD_POW |
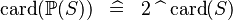 |
A | |
| * | SIMP_CARD_BUNION |
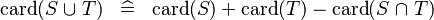 |
A | |
SIMP_CARD_SETMINUS |
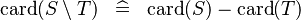 |
with hypotheses 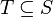 and either and either 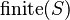 or or 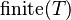 |
A | |
SIMP_CARD_SETMINUS_SETENUM |
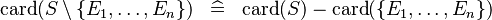 |
with hypotheses 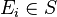 for all for all 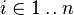 |
A | |
| * | SIMP_CARD_CONVERSE |
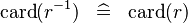 |
A | |
| * | SIMP_CARD_ID |
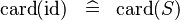 |
where 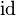 has type has type 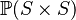 |
A |
| * | SIMP_CARD_ID_DOMRES |
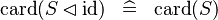 |
A | |
| * | SIMP_CARD_PRJ1 |
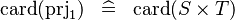 |
where 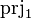 has type has type 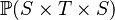 |
A |
| * | SIMP_CARD_PRJ2 |
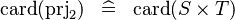 |
where 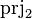 has type has type 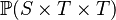 |
A |
| * | SIMP_CARD_PRJ1_DOMRES |
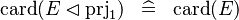 |
A | |
| * | SIMP_CARD_PRJ2_DOMRES |
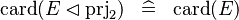 |
A | |
| * | SIMP_CARD_LAMBDA |
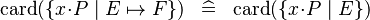 |
where  is a maplet combination of bound identifiers and expressions that are not bound by the comprehension set (i.e., is a maplet combination of bound identifiers and expressions that are not bound by the comprehension set (i.e.,  is syntactically injective) and all identifiers bound by the comprehension set that occur in is syntactically injective) and all identifiers bound by the comprehension set that occur in 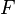 also occur in also occur in  |
A |
| * | SIMP_LIT_CARD_UPTO |
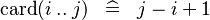 |
where 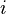 and and 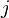 are literals and are literals and 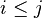 |
A |
SIMP_TYPE_CARD |
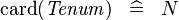 |
where 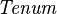 is a carrier set containing is a carrier set containing 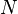 elements elements |
A | |
| * | SIMP_LIT_GE_CARD_1 |
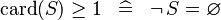 |
A | |
| * | SIMP_LIT_LE_CARD_1 |
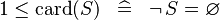 |
A | |
| * | SIMP_LIT_LE_CARD_0 |
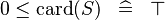 |
A | |
| * | SIMP_LIT_GE_CARD_0 |
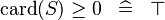 |
A | |
| * | SIMP_LIT_GT_CARD_0 |
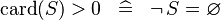 |
A | |
| * | SIMP_LIT_LT_CARD_0 |
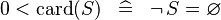 |
A | |
| * | SIMP_LIT_EQUAL_CARD_1 |
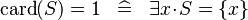 |
A | |
| * | SIMP_CARD_NATURAL |
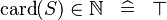 |
A | |
| * | SIMP_CARD_NATURAL1 |
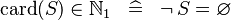 |
A | |
| * | SIMP_LIT_IN_NATURAL |
 |
where 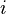 is a non-negative literal is a non-negative literal |
A |
| * | SIMP_SPECIAL_IN_NATURAL1 |
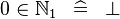 |
A | |
| * | SIMP_LIT_IN_NATURAL1 |
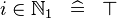 |
where 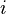 is a positive literal is a positive literal |
A |
| * | SIMP_LIT_UPTO |
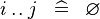 |
where 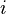 and and 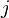 are literals and are literals and 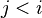 |
A |
| * | SIMP_LIT_IN_MINUS_NATURAL |
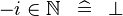 |
where 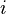 is a positive literal is a positive literal |
A |
| * | SIMP_LIT_IN_MINUS_NATURAL1 |
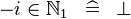 |
where 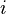 is a non-negative literal is a non-negative literal |
A |
| * | DEF_IN_NATURAL |
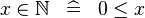 |
M | |
| * | DEF_IN_NATURAL1 |
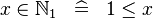 |
M | |
| * | SIMP_LIT_EQUAL_KBOOL_TRUE |
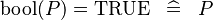 |
A | |
| * | SIMP_LIT_EQUAL_KBOOL_FALSE |
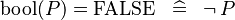 |
A | |
| * | SIMP_KBOOL_LIT_EQUAL_TRUE |
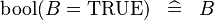 |
A | |
| * | DEF_EQUAL_MIN |
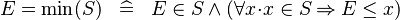 |
where  non free in non free in 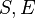 |
M |
| * | DEF_EQUAL_MAX |
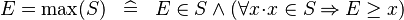 |
where  non free in non free in 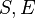 |
M |
| * | SIMP_SPECIAL_PLUS |
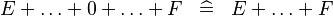 |
A | |
| * | SIMP_SPECIAL_MINUS_R |
 |
A | |
| * | SIMP_SPECIAL_MINUS_L |
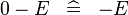 |
A | |
| * | SIMP_MINUS_MINUS |
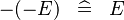 |
A | |
| * | SIMP_MINUS_UNMINUS |
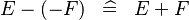 |
where 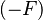 is a unary minus expression or a negative literal is a unary minus expression or a negative literal |
M |
| * | SIMP_MULTI_MINUS |
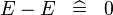 |
A | |
| * | SIMP_MULTI_MINUS_PLUS_L |
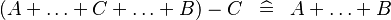 |
M | |
| * | SIMP_MULTI_MINUS_PLUS_R |
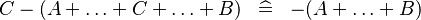 |
M | |
| * | SIMP_MULTI_MINUS_PLUS_PLUS |
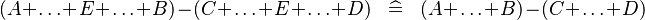 |
M | |
| * | SIMP_MULTI_PLUS_MINUS |
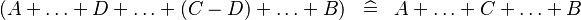 |
M | |
| * | SIMP_MULTI_ARITHREL_PLUS_PLUS |
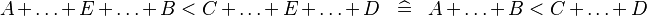 |
where the root relation (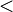 here) is one of here) is one of 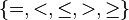 |
M |
| * | SIMP_MULTI_ARITHREL_PLUS_R |
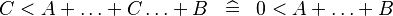 |
where the root relation (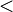 here) is one of here) is one of 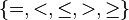 |
M |
| * | SIMP_MULTI_ARITHREL_PLUS_L |
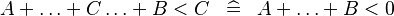 |
where the root relation (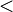 here) is one of here) is one of 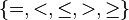 |
M |
| * | SIMP_MULTI_ARITHREL_MINUS_MINUS_R |
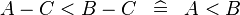 |
where the root relation (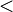 here) is one of here) is one of 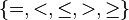 |
M |
| * | SIMP_MULTI_ARITHREL_MINUS_MINUS_L |
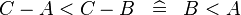 |
where the root relation (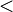 here) is one of here) is one of 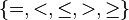 |
M |
| * | SIMP_SPECIAL_PROD_0 |
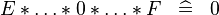 |
A | |
| * | SIMP_SPECIAL_PROD_1 |
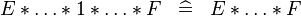 |
A | |
| * | SIMP_SPECIAL_PROD_MINUS_EVEN |
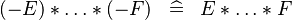 |
if an even number of  |
A |
| * | SIMP_SPECIAL_PROD_MINUS_ODD |
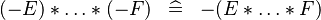 |
if an odd number of  |
A |
| * | SIMP_LIT_MINUS |
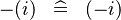 |
where 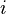 is a literal is a literal |
A |
| * | SIMP_LIT_EQUAL |
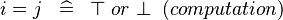 |
where 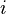 and and 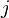 are literals are literals |
A |
| * | SIMP_LIT_LE |
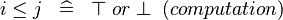 |
where 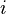 and and 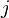 are literals are literals |
A |
| * | SIMP_LIT_LT |
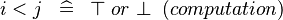 |
where 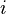 and and 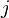 are literals are literals |
A |
| * | SIMP_LIT_GE |
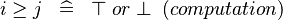 |
where 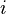 and and 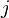 are literals are literals |
A |
| * | SIMP_LIT_GT |
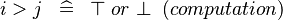 |
where 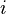 and and 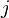 are literals are literals |
A |
| * | SIMP_DIV_MINUS |
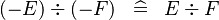 |
A | |
| * | SIMP_SPECIAL_DIV_1 |
 |
A | |
| * | SIMP_SPECIAL_DIV_0 |
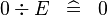 |
A | |
| * | SIMP_SPECIAL_EXPN_1_R |
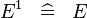 |
A | |
| * | SIMP_SPECIAL_EXPN_1_L |
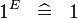 |
A | |
| * | SIMP_SPECIAL_EXPN_0 |
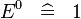 |
A | |
| * | DEF_EXPN_STEP |
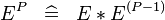 |
with an additional PO 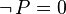 |
M |
| * | SIMP_MULTI_LE |
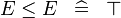 |
A | |
| * | SIMP_MULTI_LT |
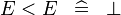 |
A | |
| * | SIMP_MULTI_GE |
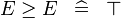 |
A | |
| * | SIMP_MULTI_GT |
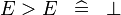 |
A | |
| * | SIMP_MULTI_DIV |
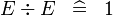 |
A | |
| * | SIMP_MULTI_DIV_PROD |
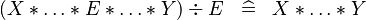 |
A | |
| * | SIMP_MULTI_MOD |
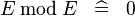 |
A | |
DISTRI_PROD_PLUS |
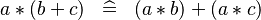 |
M | ||
DISTRI_PROD_MINUS |
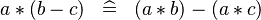 |
M | ||
DERIV_NOT_EQUAL |
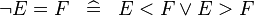 |
 and and 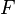 must be of Integer type must be of Integer type |
M |
Extension Proof Rules
Rules that are marked with a * in the first column are implemented in the latest version of Rodin. Rules without a * are planned to be implemented in future versions. Other conventions used in these tables are described in The_Proving_Perspective_(Rodin_User_Manual)#Rewrite_Rules.
Rewrite Rules
| Name | Rule | Side Condition | A/M | |
|---|---|---|---|---|
| * | SIMP_SPECIAL_COND_BTRUE |
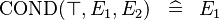 |
A | |
| * | SIMP_SPECIAL_COND_BFALSE |
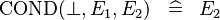 |
A | |
| * | SIMP_MULTI_COND |
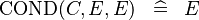 |
A |
Inference Rules
| Name | Rule | Side Condition | A/M | |
|---|---|---|---|---|
| * | DATATYPE_DISTINCT_CASE |
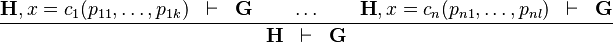 |
where  has a datatype has a datatype 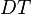 as type and appears free in as type and appears free in 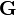 , , 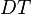 has constructors has constructors 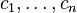 , parameters , parameters 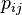 are introduced as fresh identifiers are introduced as fresh identifiers |
M
|
| * | DATATYPE_INDUCTION |
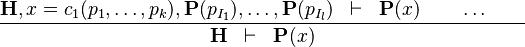 |
where  has inductive datatype has inductive datatype 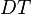 as type and appears free in as type and appears free in 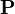 ; ; 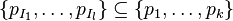 are the inductive parameters (if any); an antecedent is created for every constructor are the inductive parameters (if any); an antecedent is created for every constructor 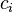 of of 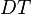 ; all parameters are introduced as fresh identifiers; examples here ; all parameters are introduced as fresh identifiers; examples here |
M |